高三数学综合测试题—（3）

高中学生学科素质训练

　

高三数学综合测试题—（3）

　　本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间120分钟。

第Ⅰ卷（选择题，共60分）

一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1．设集合　　　　　　　　 （　　）

　　　 A．{0,1}　　　　　　　　　　　　　　　　　　　　　　　　 B．{(0,0),(1,1)}　　　　

　　　 C．P　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．M

2．若圆锥的侧面母线长为2，轴截面的面积是，则圆锥的底面半径为　　　　　　　（　　）

　　　 A．1或2　　　　　　　　 　　　　　　　　　　　　　　　　B．　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　D．1或

3．复数icos3的三角形式为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　 B．

　　　 C． 　　　　　　　　　D．

4．甲、乙两人独立地对同一目标各射击一次，其命中率分别是0.6和0.5，现已知目标被击中，则它是甲射中的概率是 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．0.6　　　　　　　　　　　　　　　　　　　　　　　　　　 B．　　　　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　　 D．

5．在复平面上，方程所表示的轨迹是　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．四个点　　　　　　　 B．两条直线　　　　　　C．一个圆　　　　　　　 D．两个圆

6．已知三条直线，设l₁与l₂的夹角为，与l₃的夹角为，则等于　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．45°　　　　　　　 　　　　　　　　　　　　　　　　　 B．75°　　　　　　　　　

　　　 C．105°　　　　　　　　　　　　　　　　　　　　　　　　 D．135°

7．已知（1—2x）ⁿ的展开式中，奇数项的二项式系数之和为64，则该二项式展开式的中间项为　　　　　　　　　　　（　　）

　　　 A．560x⁴　　　　　　　　　　　　　　　　　　　　　　　　 B．-280x³　　　　　　　　

　　　 C．280x³或-560x⁴　　　　　　　　　　　　　　　　　　D．-280x³或560x⁴

8．已知数列{a_n}满足则下列结论正确的是　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　D．

9．已知两点A（-2，0），B（0，2），点C是圆x²+y²-2x=0上任意一点，则△ABC面积的最小值是　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　B．　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　D．

10．如图，在正方体ABCD—A₁B₁C₁D₁中，A₁B₁C₁D₁中，A₁B与平面BB₁D₁D所成的角的大小是　　　　　　　　 （　　）

　　　 A．90°　　　　　　　　　 B．60°

　　　 C．45°　　　　　　　　　 D．30°

11．从6种小麦品种中选出4种，分别种植在不同土质的4块土地上进行试验，已知1号、2号小麦品种不能在试验田甲这块地上种植，则不同的种植方法有　　　　　 （　　）

　　　 A．114种　　　　　　　　 B．180种　　　　　　　　 C．240种　　　　　　　　D．300种

12．设f(x)(x∈R)为偶函数，且，

　　f(x)=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　)

　　　 A．x+4　　　　　　　　　　　　　　　　　　　　　　　　　 B．2-x　　　　　　　　　　

　　　 C．3-x+1　　　　　　　　　　　　　　　　　　　　　　　　D．2+x+1

第Ⅱ卷（非选择题，共90分）

二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上）

13．设等差数列{a_n}共有3n项，它的前2n项之和是100，后2n项之和是200，则该等差数列的中间n项之和等于　　　　　  .

14．抛掷两个骰子，当至少有一个的点数的3的倍数时，就说这次试验成功，设在50次试验中成功的次数为，则E=　　　　　  ，D=　　　　　  （精确到0.01）

15．人造地球同步通讯卫星的运行轨道是圆，卫星距地面高度是19200km，地球半径取6400km，若电磁波是直线传播，那么卫星覆盖的地球表面区域（是一个球冠）的面积与地球表面积之比是　　　　　 .

16．关于函数,有下列命题：

　　　 ①由；

　　　 ②的表达式可改写为

　　　 ③图象关于点对称；

　　　 ④的图象关于直线

　　　 其中正确的命题序号是　　　　　　　 （注：把你认为正确的命题序号都填上）.

三、解答题（本大题共6小题，共74分解答应写出文字说明、证明过程或演算步骤）

17．（本小题满分12分）已知a>0且a≠1，解关于x的不等式

.

18．（本小题满分12分）

求a是不为零的常数，函数f(x)满足关系式：

(1)求f(x);(2)若曲线y=f(x)从x=1到x=2的部分绕x轴旋转一周所得立体的体积是，试确定a的值.

19．（本小题满分12分）

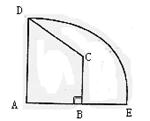
如图，直角梯形ABCD中，AD=3，AB=4，BC=，曲线DE上任一点到A、B两点距离之和都相等.

（Ⅰ）适当建立坐标系，求曲线DE的方程；

（Ⅱ）过C点能否作一条与曲线DE相交且以C为中点的弦，如果不能，请说明理由，如果能，求出弦所在直线的方程.

20．（本小题满分12分）

假设国家收购某种农产品的价格是120元/担，其中征税标准为每100元征8元（叫收税率为8个百分点，即8%）计划可收购m万担，为了减轻农民的负担，决定税率降低x个百分点，预计收购量增加2x个百分点.

（Ⅰ）写出税收y（万元）与x的函数关系式；

（Ⅱ）要使此项税收在税率调节后不低于原计划的78%，试确定x的范围.

21．（本小题满分12分）

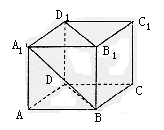
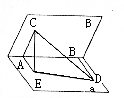
在60°的二面角的棱上，有A、B两点，线段AC、BD分别在二面角的两个面内，且都垂直于AB，已知AB=4，AC=6，BD=8.

（1）求CD的长度；

（2）求CD与平面所成的角.

22．（本小题满分14分）

设函数y=f(x)定义在R上，对于任意实数m、n,f(m+n)=f(m)·f(n)恒成立，且x>0时，0<f(x)<1.

（Ⅰ）求证：f(0)=1，且当x<0时，f(x)>1;

（Ⅱ）求证：f(x)在R上递减;

（Ⅲ）设集合，若，求a的取值范围.

高三数学综合测试题参考答案

（三）

一、选择题1．D　2．D　3．D　4．C　5．C　6．D　7．D　8．A　9．A　10．D　11．C　12．C

二、填空题13．75　　　 14．27.78,12.35　　15．3：8　　 16．②、③

三、解答题17．原不等式等价于下列不等式组

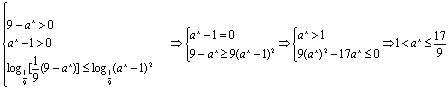
当a>1时，原不等式的解集为] 当0<a<1时，原不等式的解集为

18．（1）

，再积分得：

，

将代入条件得

（2）

19．

（Ⅰ）取AB中点O为原点，AB所在直线为x轴，建立直角坐标系，由题意，曲线DE为一段椭圆弧.　　

（Ⅱ）曲线DE与y轴交点M（0，），与x轴交点N（4，0），显然C（2，）为M、N中点，所以弦MN即为所求.其所在直线方程为

20．（Ⅰ）由题设知，调节后的税率为（8-x）%，预计可收购m(1+2x%)担，总金额为120m(1+2x%)万元，依题意得y=120m(1+2x%)（8-x）%，即

（Ⅱ）原计划税收为120m·8%万元，依题意有

解之，得

21．（1）因为，故有

，

因为CA⊥AB，BD⊥AB，所以

所以.

（2）过C作CE⊥平面α于E，连接AE、CE在△ACE中，CE=6sin60°=3，连接DE，则∠CDE就是CD与平面α所成角.

22．（Ⅰ）在故f(0)=1.

设

（Ⅱ）

代入即

所以，f(x)为R上的减函数.

（Ⅲ）由（Ⅱ）知f(x)为R上的减函数.

由

相离或相切……

于是