高三数学高考模拟题（一）
一. 选择题（12小题，共60分，每题5分）
1. 已知集合
，那么集合P的子集共有( )
A. 3个 B. 7个 C. 8个 D. 16个
2. 函数
的反函数的图象大致是( )
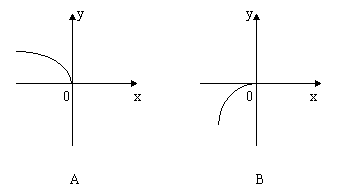
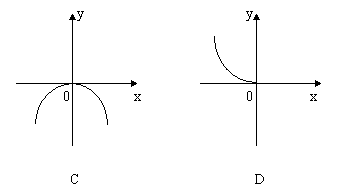
3. 已知直线
与平面
，下面给出四个命题：
其中正确命题是( )
A. (4) B. (1)(4) C. (2)(4) D. (2)(3)
4. 设
等于( )
5. 设
之间的大小关系是( )
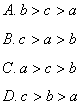
6. 
展开式的系数和为
展开式的系数和为
等于( )
7.椭圆
，椭圆的两个焦点为
的面积是( )
A. 96 B. 48 C. 24 D. 12
8. 已知椭圆
的一条准线的方程为
则实数t的值为( )
A. 7和－7 B. 4和12 C. 1和15 D. 0
9. 函数
的单调递减区间是( )
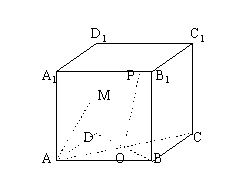
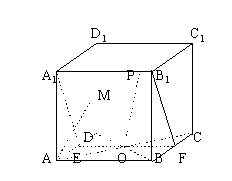
10. 如图在正方体ABCD－
中，M是棱DD1的中点，O为底面ABCD的中心，P为棱
上任意一点，则直线OP与直线AM所成的角( )
A. 是
B. 是
C. 是
D. 与P点位置有关
11. 在平面直角坐标系中，由六个点O(0，0)、A(1，2)、B(－1，－2)、C(2，4)、D(－2，－1)、E(2，1)可以确定不同的三角形共有( )
A. 14个 B. 15个 C. 16个 D. 20个
12. 过点
平行，则
间的距离是( )
二. 填空题（4小题，共16分，每题4分）
13. 函数
的最小正周期是_________。
14. 抛物线
上一点M到焦点的距离为a，则点M到y轴的距离为_______。
15. 若E、F、G、H分别是三棱锥A－BCD的AB、BC、CD、DA棱的中点，则三棱锥A－BCD满足条件________时，四边形EFGH是矩形(注：填上你认为正确的一种条件即可，不必考虑所有可能的情况)
16. 在平面内，
(1)到两个定点的距离的和等于常数的点的轨迹是椭圆；
(2)到两个定点的距离的差的绝对值为常数的点的轨迹是双曲线；
(3)到定直线
和定点
的距离之比为
的点的轨迹是双曲线；
(4)到定点
和定直线
的距离之比为
的点的轨迹是椭圆。
请将正确命题的代号都填在横线上__________。
三. 解答题：本大题共6小题；共74分，解答题应写出文字说明、证明过程或演算步骤。
17. (本小题满分12分)
已知
，复数
时，
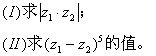
18. (12分)设集合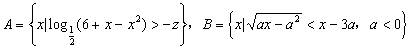
，求使
的取值范围。
19. (12分)某集团投资兴办甲、乙两个企业，1998年甲企业获得利润320万元，乙企业获得利润720万元，以后每年企业的利润甲以上年利润1.5倍的速度递增，而乙企业是上年利润的
，预期目标为两企业年利润之和是1600万元，从1998年年初起，
(I)哪一年两企业获利之和最小；
(II)需经过几年即可达到预期目标(精确到一年)
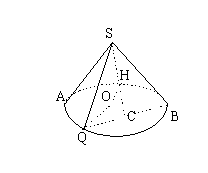
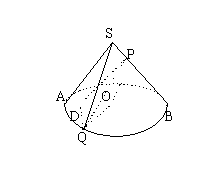
20. (12分)如图，圆锥的轴截面是等腰
为底面圆周上一点，
(I)若QB的中点为C，
(II)若
求此圆锥的体积。
(III)若二面角A－SB－Q为
。
21. (13分)设F1是椭圆C1：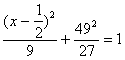
的左焦点M是C1上任意一点，P是线段
上的点且满足
仅有两个交点时，的斜率的取值范围。
(III)过A与F1的直线交C2于BC，求
的面积。(F2为C2的右焦点)
22. (13分)已知函数
且
对定义域中任意x都成立。
(I)求函数
的解析式
(II)若数列
满足当n=1时，
时，
试给出数列
的通项公式，并用数学归纳法证明。
【试题答案】
1.
2. 
3. A
4.
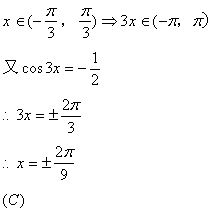
5.
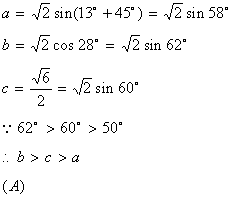
6.
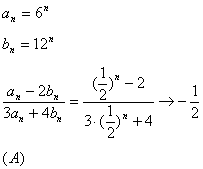
7．
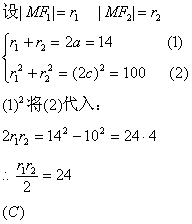
8.
中心(0，t)
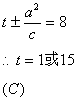
9.
10.
11.
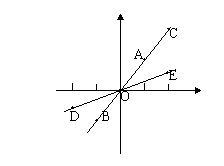
O、A、B、C四点共线，D、O、E三点共线
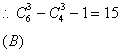
12. 注意M点在⊙上，
13.
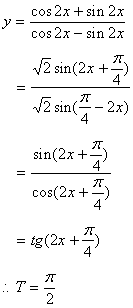
14.
15.
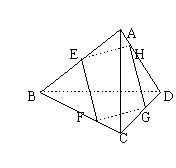
16.
(1)常数大于两定点距离时，才是椭圆
(2)常数小于两定点距离时，才是双曲线
由定义可知(3)(4)正确。
17.
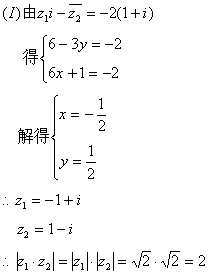
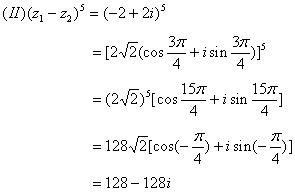
18.
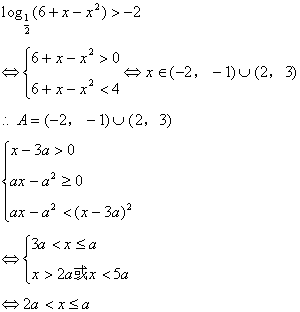
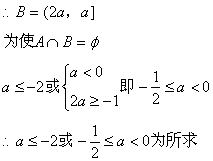
19. 设98年为第1年则第n年甲企业获利
乙企业获利720
(I)设第n年两企业获利之和最小
(II)设经过n年两企业可达到预期目标
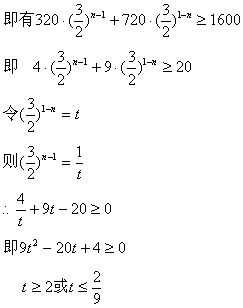
20.
21.
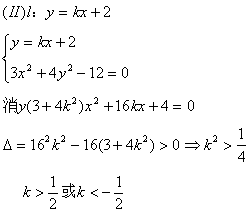
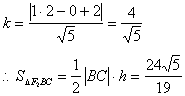
22.
