高三数学联考试题
第I卷
一、选择题
1、设集合
若
B，则实数
的取值范围是（ ）
A．
B、
C、
D、
2、已知函数
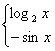
，那么
的值为（ ）
A、0 B、1 C、
D、
3、设
是两个不共线的向量，则向量
与向量
共线的弃要条件是（ ）
A．
B、
C、
D、
4、数列
是首项为100，公差为-3的等差数列，则
的最大值为（ ）
A．1718 B、1717 C、1716 D、1715
5、若
，
，则（ ）
A、
B、
C、
D、
6、如果函数
那么
在区间（ ）
A、
上是增函数 B、
上是增函数
C、上是减函数
D、
上是增函数
7、如果
，那么
的取值范围是（ ）
A、
B、
C、
D、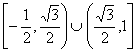
8、函数
的图象与函数
的图象在区间
上（ ）
A、没有交点 B、一定有两个交点
C、有且只有一个交点 D、至少有一个交点
9、（理科）已知函数
，则
为（ ）
A、奇函数且为周期函数 B、奇函数非周期函数
C、偶函数且为周期函数 D、偶函数非周期函数
（文科）一个直角三角形三内角的正弦值成等比数列，其最小内角的正弦值是（ ）
A、
B、
C、
D、
10、（理科）若
为非负实数且
，则下列结论正确的是（ ）
①
②
③
A、①③ B、①② C、②③ D、只有①
（文科）若
，
，则在下面关系中一定成立的是（ ）
A、
B、
C、
D、
11、已知数列满足
，则下列结论正确的是（ ）
A、
B、
C、
D、
12、甲、乙两水果基地分别生产有水果300吨和750吨，A、B、C三个城市需求量分别是200吨、450吨和400吨。甲运往A、B、C三地的费用分别为每吨6元、3元、5元；乙运往A、B、C三地的费用分别为每吨5元、9元、6元，现将这批水果运往A、B、C三个城市的最低运费为（ ）
A、4560元 B、5650元 C、5860元 D、6850元
第II卷
二、填空题
13、在等比数列中，若
，则
。
14、已知
，
和
的夹角是
，要使
与垂直，则
。
15、已知
，当
时，
恒成立，则实数
的取值范围是 。
16、函数
的定义域为
，值域为
，且在定义域上是单调函数，写出一个这样的函数的解析式 。
三、解答题
17、解关于
的不等式
18、已知
，若
时，的最大值为
，求的值。
19、已知向量
且
满足关系式
（1） 用表示、的数量积；
（2） 求
的最小值及此时、的夹角
。
20、为了保护三峡库区的生态环境，凡是坡度在
以上荒坡地都要绿化造林，经初步统计，在三峡库区内坡度大于的荒坡地面积约有2640万亩，若从2003年春节开始绿化造林，第一的绿化造林120万亩，以后每年比前一年多绿化造林60万亩。
（1）若所绿化造林的荒坡地全部成功，问到哪一年可使库区以上的荒坡地全部绿化造林？
（2）若每万亩绿化造林所植树苗的木材量平均为0.1万立方米，每年树林木材量的自然增长率为20%，那么当整个库区以上的荒坡地全部绿化造林完毕后的那一年年底，一共有木材量多少万立方米（保留1位小数）？
（参考数据
）
21、
（文科）已知函数
的图象与函数
的图象关于点
对称
（1）求
的值；
（2）若
在区间
上减函数，求实数的取值范围。
（理科）函数对一切实数
均有
成立，且
（1）求
的值；
（2）当
时，
恒成立，求的取值范围。
22、
（理科）设
（1）
若和在
上满足：当
时有
且
，求在
上的反函数
；
（2）
对于（1）中
设实数满足
，求证：
。
（文科）已知定义在R上的函数满足
且当
时，
（1）在区间
上是否存在反函数，若存在求出反函数，若不存在，请说明理由；
（2）求在
上的解析式。
答案
一、选择题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | A | B | C | B | B | D | C（B） | A（C） | C | B |
二、填空题
13、4 14、2 15、
16、
或
或
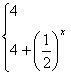
等。
三、解答题。
17、解：
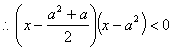
讨论：
当
，即
或
时，不等式为
或
故不等式的解集为：
当
，即
时
不等式的解集为：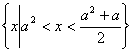
当
，即
或
时
不等式的解集为：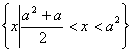
18、解：
由
得
故
解得：
19、解：（1）
即
又
故 
且
（2）
当
时 
此时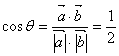 
所以 的夹角
20、解：（1）设第一年绿化面积为
万亩，以后各年绿化面积依次为
万亩、
万亩……
依题意数列是第一等差数列且
解得：
到2010年可使库区以上荒地全部绿化完
（2）设2010年底共有木材量为S万立方米
那么：
=
令 
（2）—（1）得：
故
（万立方米）
到2010到底一共有木材量543.6万立方米
21、（文科）
（1）设
为函数图象上一点，点P关于的对称点为
则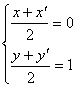
点Q在函数的图象上
即
和函数
比较知
（2）
设 
则题意：
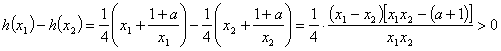
对一切
恒成立
对一切
恒成立
即
（理科）
（1）
令
得 
又
（2）由（1）知
，令
得
即
当时，
即
要使时，
恒成立
而当时，时，则
，显然不可能保证上述不等式成立
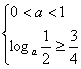解得: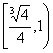
22、（理科）
（1）
当且仅当
即
时取等号
又
又
且
当
时，则
（2）
又 
而
故 
（文科）
（1）
当
时，
设 
故 
函数在上单增，且
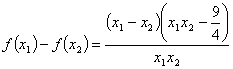
，故存在反函数
由
解得：
或
（舍去）（
）
（2）
令 
则
令 
则
故是以4为周期的周期函数
当
时，则
