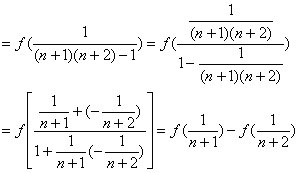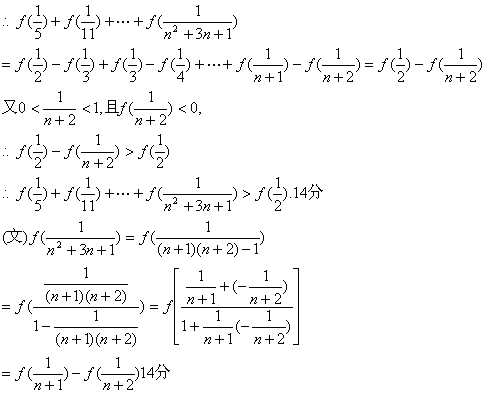高三数学模拟考试试题（三）答案
一、1.A 2.B 3.D 4.D 5.C 6.(理)A (文)B 7.C 8.B 9.A 10.A 11.D 12.C
二、13.8 14.y2-16x2+8y=0(y≠0) 15.①②
16.BC1，CD，A1D1或CC1，BD，A1D1或BC，C1D1，A1D或BC，DD1，A1C1(任选填一种)
三、17.解：(Ⅰ)由f(0)=2a=2,∴a=1,f(
∴b=2
∴f(x)=2cos2x+2sinxcosx=sin2x+cos2x+1=
∴f(x)最大值为
+1，最小值为1-.6分
(Ⅱ)若f(α)=f(β),则sin(2α+
)=sin(2β+),
∴2α+=2kπ+2β+或2α+=2kπ+π-(2β+),即α-β=kπ(舍去)或α+β=
kπ+,k∈Z,
∴tan(α+β)=tan(kπ+)=1. 12分
18.解：(Ⅰ)由已知，有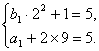
解得b1=1,a1=-13. 2分
从而an=-13+(n-1)·2=2n-15,bn=1×2n-1=2n-1,
cn=anbn=(2n-15)2n-1 5分
(Ⅱ)∵Sn=a1b1+a2b2+…+anbn, ①
∴aSn=a1b2+a2b3+…+an-1bn+anbn+1. ②7分
①-②得(1-q)Sn=a1b1+d(b2+b3+…+bn)-anbn+1=a1b1+d·
-anbn+1
=-13+2·
-(2n-15)·2n=-［(2n-17)·2n+17］,
∴Sn=(2n-17)·2n+17.10分
∴
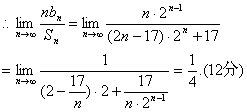
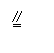
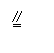
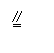19.解：(Ⅰ)取CD中点G，连AG，FG，则有FG AB 
.
∴AG BF,又△ACD为正三角形，
∴AG⊥CD，又DE⊥平面ACD，
∴FG⊥平面ACD.
∴FG⊥AG.∴AG⊥平面CDE
∴BF⊥平面CED.4分
(Ⅱ)VABCDE=VB—ACD+VB—CDE=
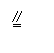(Ⅲ)由(1)知AB 
DE,延长DA，EB交于P，连PC，则可证得A，B分别为PD，
PE中点，∴PC∥BF∥AG，
∴PC⊥平面CDE，∴∠DCE为平面BCE和平面ACD所成二面角的平面角，又∠DCE=45°,即所成锐二面角为45°.12分
20.解：设羊毛衫出售价格为x元/件，购买人数为y人，最高价格为x0,则存在
a,b使y=ax+b.
由条件知：a＜0且0=ax0+b
∴x0=-
.因此y=a(x-x0)=-a(x0-x),商场利润s=y(x-100)=-a(x0-x)(x-100)≤-a(
当且仅当x0-x=x-100,即x=50+
时“=”成立. 6分
因此商场定价x=50+时能获最大利润，设旺、淡季的最高价格分别为a,b.淡季能获最大利润的价格为c，则140=50+
,a=180, 9分
∴b=
a=120.∴c=50+
=110(元/件)12分
21.(Ⅰ)证明：以直线AB为x轴，AB的中点为原点建立直角坐标系，则点A，B的坐标分别为(-1，0)，(1，0).
∵l为MB的垂直平分线，
∴PM=PB，PA+PB=PA+PM=MA=4.
∴P点的轨迹是以A，B为两个焦点，长轴长为4的椭圆，其方程为
根据椭圆的定义可知，点P到点B的距离与点P到直线k:x=4(恰为椭圆的右准线)的距离之比为离心率e=.4分
(Ⅱ)解：m=PA·PB≤(
=4,
当且仅当PA=PB时，m最大，这时P点的坐标为(0，
)或(0，-).8分
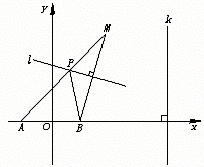
(Ⅲ)解：由PA-PB=1及PA+PB=4，得
PA=
，PB=
.
又AB=2，所以△APB为直角三角形，∠ABP=90°.故cosAPB=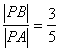
.
22.解：(Ⅰ)x,y∈(-1,1).
f(x)+f(y)=f(
),
令x=y=0,得f(0)=0.
令y=-x,得f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x)
∴f(x)在(-1，1)上是奇函数.4分
(Ⅱ)设-1＜x1＜x2＜0,则
f(x1)-f(x2)=f(x1)+f(-x2)=f(
),
∵x1-x2＜0,1-x1x2＞0,
∴-1＜＜0.
x∈(-1,0)时f(x)＞0
∴f(x1)-f(x2)＞0,从而f(x)在(-1，0)上是单调减函数. 8分
(Ⅲ)(理)∵f(
)
