高三数学模拟试卷（文科）
一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)
1. 已知集合A=
B=
则能使A
B成立的实数
的取值范围是 （ ）
（A）
（B）
（C）
（D）Φ
2.使不等式x+1＜2x成立的充分不必要条件是
A.－
＜x＜1 B.x＞－
C.x＞1 D.x＞3
3.函数y=(cosx－
sinx)(sinx－cosx)的最小正周期为
A.4π B.2π C.π D.
4. 与双曲线
－
＝１有相同离心率的曲线方程可以是
A. +＝１
B.
－＝１
C. －＝１
D.
+＝１
5.已知f(x)=
,a、b为两个不相等的正实数，则下列不等式正确的是
A.f(
)＞f(
)＞f(
) B.f()＞f()＞f()
C.f()＞f()＞f() D.f()＞f()＞f()
6.下列四个函数：y=tg2x,y=cos2x,y=sin4x,y=ctg(x+
)，其中以点(，0)为中心对称点的三角函数有
A.1个 B.2个 C.3个 D.4个
7.如图，在正方体ABCD—A１Ｂ１Ｃ１Ｄ１中，EF是异面直线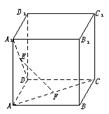
AC与A１Ｄ的公垂线，则由正方体的八个顶点所连接的直线中，与EF平行的直线
A.有且仅有一条 B.有二条
C.有四条 D.不存在
8.在轴截面是直角三角形的圆锥内，有一个侧面积最大的内接圆柱，则内接圆柱的侧面积与圆锥的侧面积的比值是
A.1∶2 B.1∶2
C.1∶ D.1∶4
9.从集合｛1,2,3,…，10｝中任意选出三个不同的数，使这三个数成等比数列，这样的等比数列个数为
A.3 B.4 C.6 D.8
10.若函数f(x)=ax－1的反函数图象经过点(4，2)，则函数g(x)=loga
的图象是
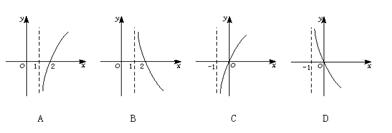
11.三角形中，三边a、b、c所对应的三个内角分别是A、B、C，若lgsinA、lgsinB、lgsinC成等差数列，则直线xsin２A+ysinA=a与直线xsin２B+ysinC＝c的位置关系是
A.平行 B.相交但不垂直
C.垂直 D.重合
12.甲、乙两工厂2002年元月份产值相同，甲厂的产值逐月增加，且每月增加的产值相等，乙厂的产值也逐月增加，且每月增长的百分率相等，已知2003年元月份两厂的产值相等，则2002年7月份产值高的工厂是
A.甲厂 B.乙厂 C.产值一样 D.无法确定
二、填空题（共16分）
13.若(x２－
)n的展开式中含x的项为第6项，设(1－x+2x２)n＝a０+a１x+a２x２+…+a2nx2n，则
a１+a２＋a３+…+a2n＝______.
14.已知奇函数f(x)在(0，+∞)内单调递增，且f(2)=0，则不等式(x－1)·f(x)＜0的解集是______.
15.已知数列｛an｝同时满足下面两个条件：(1)不是常数列；(2) an＝a1，则此数列的一个通项公式可以是______.
16. 若过点（
总可以作两条直线和圆（
相切，则实数
的
取值范围是 .
三、解答题(本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤)
17.（12分） 设复数z满足2z+5=
+10.
(Ⅰ）求z的值；
（Ⅱ）若
在复平面上对应的点在第一、三象限的角平分线上，求复数z .
18. （12分）如图，正三棱柱ABC－A1B1C1，各棱长都等于a, E是BB1的中点 .
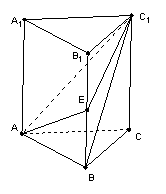（Ⅰ）求直线C1B与平面A1ABB1所成角的正弦值；
（Ⅱ）求证：平面AEC1⊥平面ACC1A1.
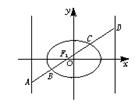19.（12分）已知椭圆
+
＝１(1≤m≤4)，过其左焦点F１且倾斜角 为
的直线与椭圆及其准线分别交于A、B、C、D(如图)，记f(m)=AB－CD
(Ⅰ)求f(m)的解析式；
(Ⅱ)求f(m)的最大值和最小值.
20.（12分）某房屋开发公司用128万元购得一块土地，欲建成不低于五层的楼房一幢，该楼每层的建筑面积为1000平方米，楼房的总建筑面积(即各层面积之和)的每平方米的平均建筑费用与楼层有关，若该楼建成x层时，每平方米的平均建筑费用用f(x)表示，且f(n)=f(m)(1+
)(其中n＞m,n∈N)，又知建成五层楼房时，每平方米的平均建筑费用为400元，为了使该楼每平方米的综合费用最省(综合费用是建筑费用与购地费用之和)，公司应把该楼建成几层?
21.（12分）设函数f(x)=
，数列｛an｝满足：a１＝3f(1),an+1＝
(Ⅰ)求证：对一切自然数n，都有＜an＜+1成立；
(Ⅱ)问数列｛an｝中是否存在最大项或最小项?并说明理由.
22.（14分）已知函数f(x)=
－x
(Ⅰ)当a=－1时，求f(x)的最值;
(Ⅱ)求不等式f(x)＞0的解.
文科模拟考参考答案
一、1.B 2.D 3.C 4.B 5.A 6.D 7.A 8.B 9.D 10.D 11.D 12.A
二、13.255 14.(－2,0)∪(1,2) 15.
16.
三、17.解：设z=x+yi (x ,y ∈R)，则……1分 （Ⅰ）(2x+5)2+(2y)2=(x+10)2+y2 (4分)
得到x2+y2=25 .∴z=5 . ( 6分)
（Ⅱ）(1－2i)z=(1－2i)(x+yi)=(x+2y)+(y－2x)I 依题意，得x+2y=y－2x
∴y=－3x . ① (9分)
由（Ⅰ）知x2+y2=25 . ②由①②得
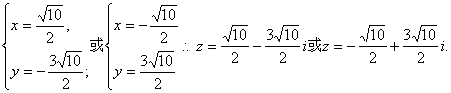(12分)
18.解：（Ⅰ）取A1B1中点M，连结C1M，BM . ∵三棱柱ABC－A1B1C1是正三棱柱，
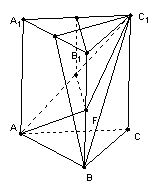∴C1M⊥A1B1 C1M⊥BB1 . ∴C1M⊥A1ABB1
. ∴∠C1BM为直线C1B与平面A1ABB1所成的角
（ 4分）
在Rt△BMC1中，C1M=
a , BC1= a ,
∴sin∠C1BM=
（ 6分）
（Ⅱ）取A1C1的中点D1，AC1的中点F，连结B1D1，EF，D1F .
则有D1F∥
AA1 ，B1E∥AA1. ∴D1F∥B1E . 则四边形D1FEB1是平行四边形，
∴EF∥B1D1 （ 8分）
由于三棱柱ABC—A1B1C1是正三棱柱，∴B1D1⊥A1C1，又平面A1B1C1⊥平面ACC1A1于A1C1，且B1D1
平面A1B1C1，∴B1D1⊥平面ACC1A1
（ 10分）
∴EF⊥平面ACC1A1
. ∵EF平面AEC1，则平面AEC1⊥平面ACC1A1. （12分）
19.解：(Ⅰ)设A、B、C、D四点的横坐标依次为x１,x２，x３,x４，
则AB＝２（x２－x1） CD＝2(x４－x３)
∴f(m)=2x２＋x３ (2分)
将直线y= (x+1)代入+＝１中
(3+4m)x２+6(m+1)x+(m－1)(3－m)=0 (6分)
∴f(m)＝2x１＋x２＝
(1≤m≤4)
(8分)
(Ⅱ)∵f(m)=3+
在［1,4］上是减函数
∴f(m)max＝f(1)＝
；f(m)min=f(4)=
(12分)
20.解：设该楼建成x层，则每平方米的购地费用为
＝
(2分)
由题意知f(5)＝400, f(x)＝f(5)(1+
)＝400(1+)
(6分)
从而每平方米的综合费用为y=f(x)+＝20（x+
）+300≥20.2
+300＝620（元），当且仅当x=8时等号成立
(10分)
故当该楼建成8层时，每平方米的综合费用最省. (12分)
21.( Ⅰ)证明：a１＝3f(1)=2，an+1＝＝
(2分)
①当n=1时，a１∈(，+1)，不等式成立
(3分)
②假设n=k时，不等式成立，即＜ak＜+1，则0＜ak－＜1
ak+1－＝
－＝
∵0＜(ak－)２＜1，2ak＞2＞0
∴0＜ak+1－＜
＜1，∴当n＝k+1时，不等式也成立
由①②可知，＜an＜+1 对一切自然数n都成立
(8分)
(Ⅱ)解：∵an＞，∴an+1－an＝
＞0
∴｛an｝是递增数列，即｛an｝中a１最小，没有最大项 (12分)
22.解：(Ⅰ)f(x)＝
－x＝－(－)２＋
(x≥－1)
∴f(x)最大值为 (4分)
|
x－a≥0
|
|
|
x－a＞x２
当a≥0时，②无解，当a＜0时，②的解为a≤x＜0(8分)
|
x≥0
x２－x+a＜0，
当Δ＝1－4a≤0时，①无解，当Δ＝1－4a＞0时，x２－x+a＜0解为
＜x＜
故a≥0时①的解为＜x＜；
当a＜0时①的解为0≤x＜ (12分)
综上所述，a≥
时，原不等式无解；当0≤a＜时，原不等式解为＜x＜，当a＜0时，a≤x＜ (14分)