高三数学模拟试题

高三数学模拟试题

一．选择题（60分）

（1）关于x的不等式的解集为R的充要条件是　　　　　　　　　 （　　 ）

(A)m＜0　　 (B)m≤－1　　　　(C)m≤0 　　　(D)m≤1

（2）函数的图象是　　　　　　　　　　　　　　　　　　　  （　 　）

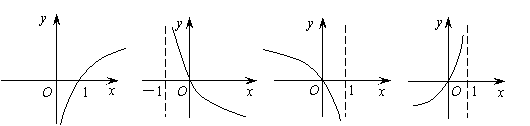(A)　　　　　　   (B) 　　　　　　　　 (C)　　　　　　　  (D)

（3）已知数列1，a₁,a₂,4成等差数列,1，b₁，b₂，b₃，4成等比数列，则的值（　 ）

（A）　　　　  （B）　　　 （C）或 　　　　　 （D）

（4）设是双曲线　　的两焦点，点P在双曲线上，，则的值等于　　　　　　　　　　　　　　  （　　）　　　　　　　　　　　　　　 

（A）1　　　　  （B）　　　　　 （C）2　　　　　 （D）

（5）若函数y＝cos2x与函数y＝sin(x＋φ)在[0,]上的单调性相同，则φ的一个值为(　　)

（A）　　　　　　 （B）　　　　　　 （C）　　　　　　 （D）

（6）函数的定义域为（0，+∞），且 那么函数 （ 　）

(A)存在极大值　　　 (B)存在极小值　　　 (C)是增函数　　　　　(D)是减函数

（7）某债券市场发行的三种债券：A种面值100元，一年到期本利共获103元。B种面值50元，半年到期，本利共50.9元。C种面值为100元，但买入时只需付97元，一年到期拿回100元。则三种投资收益比例从小到大排列为　　　　 　　　　　　　　　　（　　）

(A)BAC　　 　　　　 (B)ACB　　 　　　　  (C)ABC　　　　(D)CAB

（8）若函数y=f(x-1)是偶函数，则y=f(x)的图象关于　　　　　　　　　　　　  (　　)

(A)直线x+1=0对称　　　　　 (B)直线x-1=0对称

(C)直线x-=0对称　　　　  (D)y轴对称

（9）已知、是直线，是平面，给出以下四命题：

①；②；③；④

其中正确的命题是　　　　　　　　　　　　　  (　　)

(A)① ②　　 (B)① ② ③　　(C)① ② ④　  (D)② ③ ④

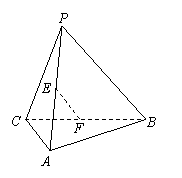
（10）如图，E、F分别是三棱锥的棱AP、BC的中点，

　　　 ，，EF=7，则异面直线AB与PC

所成的角为　　　　　　　　　　　　　　　　　　  (　　)

(A) 60⁰　　　 (B)45⁰　　　　(C) 30⁰　　　 (D)120⁰

（11）艺术体操委员会由10位女性委员与5位男性委员组成，委员会要组织6位委员出国考察学习，如果按性别作分层，并在各层依比例随机抽样，试问此考察团的组成方法的种数共有　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　 （　　）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　(A)　　　　 (B)　　　　 (C)　　　　　 (D)

（12）直线将圆分成若干块，现用5种不同的颜色给这若干块涂色，且共边的颜色不同，每块只涂一色，共有260种涂法，则m的取值范围是　（　　）　　　　　　　　　　　　　　　　　 

（A）　　（B）　　  （C）　　 （D）

二．填空题（16分）

（13）已知函数的反函数的图象的对称中心是（0，2），则a= 　　　　 .

（14）两直线与两坐标轴围成的四边形有外接

　　圆，则m的值等于　　　　  .

（15）甲、乙两位同学在连续10次数学测试中的成绩如下表：

次数 成绩	1	2	3	4	5	6	7	8	9	10
甲	80	75	95	85	70	80	85	60	90	80
乙	60	90	65	85	75	75	80	90	95	85

　 其中数学成绩比较稳定的同学是　　　　.

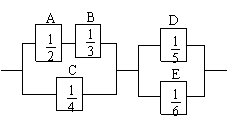
（16）如图：电路中五个方框均为保险匣。框

　　内数字为通电时保险丝被烧断的概率，

　　假定通电后保险丝是否烧断是相互独立

　　的，则通电后不断路的概率为　　　　.

三．解答题

17．(本小题满分12分)

已知向量，向量与的夹角为, 且

   （1）求向量.

　 （2）若且，，其中A、C是的内角，若三角形的三个内角A、B、C依次成等差数列，试求的取值范围.

18．(本小题满分12分)

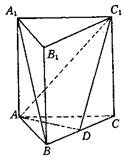
正三棱柱ABC—A₁B₁C₁的侧棱长和底面边长都等于2，D是BC上一点，

且AD⊥BC.

　　　 （1）求证：A₁B∥平面ADC₁;

　　　 （2）求截面ADC₁与侧面ACC₁A₁所

成的二面角D—AC₁—C的大小.

19．(本小题满分12分)

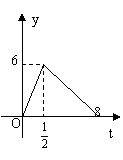
某医药研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y与时间t之间近似满足如右图所示的曲线.

（1）写出服药后y与t之间的毫升关系式；

（2）据测定：每毫升血液中含药量不少于4微克时治疗疾病有效.假定某病人一天中第一次服药为7点钟，问：一天中怎样安排服药时间、次数，效果最佳？

20．(本小题满分12分)

如图：A、B、C三点为工人宿舍区，O为工厂所在地，已知每两点之间皆有笔直公路相通（除此外无其他公路），如果O点距△ABC（∠A>∠B>∠C）三边等距离.当一辆班车将下班工人分送到A、B、C三处以后，再返回工厂时，请你设计一种方案，使行车路程最短.

21．(本小题满分12分)

已知动点与双曲线的两个焦点、的距离之和为定值，且

的最小值为．

（1）求动点的轨迹方程；

（2）若已知，、在动点的轨迹上且，求实数的取值范围．

22．（本题其中（1）、（2）12分（3）为附加题4分，满分16分）

对任意函数可构造一个数列发生器：输入数据，输出，若，则结束工作；若，则输入，输出。并依次规律继续下去，现定义 （）.

（1）若要产生一个无穷常数列，试求的值；

（2）若是的一个近似值，，试判断和中那一个更接近于？

（3）请依据以上事实，设计一种求的近似值的方案，并说明理由.

高三数学模拟试题（三）答案

一.选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	A	C	A	A	D	C	B	A	A	A	A	C

二．填空题

13．2　　　　 14．-5　　　　15．甲　　　　 16．

三．解答题

17．解：（1）设　　　　 　 　 

　　　①　　　　　　　　　又与的夹角为，

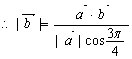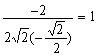
　　=　　  　 ②　　　　　 　　　　　　　　　　 联立①②得或　 或　.　　　　　　　　　　　　　

　　 （2）由题意　 知　 且

　　  　　 　　　　　　　　　　　　　　　　　　　　　　　　　　

　　  　　　

　　　　=

　　　　　　　　  = =

　　　　　　　　  = 　　　　　　　　　　　　　　　　　　　　　

　　　　

　　　　  　,  

即  ,　 　　　　　　　　　　　　　　　　　　

18．解：（1）在正三棱柱ABC—A₁B₁C₁中，

是BC的中点. 连A₁C交AC₁于E，则E是A₁C的中点，

连ED，则ED为△A₁BC的中位线.

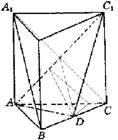　　　 　　∴ED∥A₁B.

　　　 　　又ED平面ADC₁，∴A₁B∥平面ADC

　　　 （2）过D作DM⊥AC于M，

∵正三棱柱ABC—A₁B₁C₁中，侧面ACC₁A₁⊥底面ABC，

DM底面ABC，∴DM⊥侧面ACC₁A₁，作MN⊥AC₁于N，连

ND，则根据三垂线定理知：AC₁⊥ND，∴AC₁⊥面NDM，

∴∠DNM即为二面角D—AC₁—C的平面角，在Rt△DMC中，DM=DC在Rt△ANM中，NM=AM

在Rt△DMN中，tan∠DNM=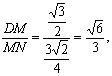即所求二面角的大小为

19．（1）有题意，得.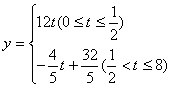

（2）设第二次服药时在第一次服药后t₁小时，则，小时.

因而第二次服药应在10点钟.

设第三次服药时在第一次服药后t₂小时，则此时血液中含药量应为两次服药后的含药量的和，即有，解得小时.

故第三次服药应在14点钟.

设第四次服药时在第一次服药后t₃小时（t₃>8），则此时第一次服进的药已吸收完，此时血液中的含药量应为第二、三次的和.

∴，小时.

故第四次服药应在17点30分.

20．解：设△ABC三边为a、b、c，工厂所在地O到宿舍区

A、B、C的距离为.

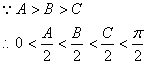
由题设知，O为△ABC的内心，设其内切圆半径为r，则

.

于是，从O点出发，按逆时针方向行车，有线路，

，

即.

若按顺时针方向行车，有线路

，

类似地也可以得到表达式.

　　又

从而

所以，选择路线或行车，这样的行车路线最短.

21．解：(1)由题意，设（），由余弦定理

得．

又·，

当且仅当时，· 取最大值，

此时取最小值，令，解得

，，∴，故所求的轨迹方程为．

（2）设，，则由，可得

，故，

∵、在动点的轨迹上，故且，

消去可得，解得，

又，∴，解得，

故实数的取值范围是．

22．解：由题意，要产生一个无穷常数列，只要令，解得，又，故，易见仅当时，可构造一个常数列；

（Ⅱ）更接近于，下面证明之：

因为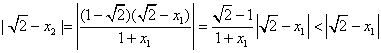

所以比更接近于.

（Ⅲ）取，依次令，则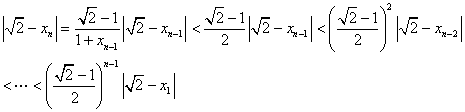

　　　表明依次更接近于，而且.

．