高三数学普通高等学校春季招生考试1
数学（文史类）
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，第I卷1至2页。第II卷3至9页，共150分，考试时间120分钟。
第I卷（选择题 共50分）
注意事项：
1. 答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上。
3. 考试结束，监考人将本试卷和答题卡一并收回。
参考公式：
三角函数的积化和差公式
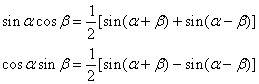
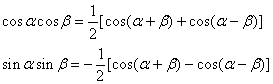
正棱台、圆台的侧面积公式
其中
分别表示上、下底面周长，
表示斜高或母线长
球体的体积公式
其中R表示球的半径
一. 选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）在函数
中，最小正周期为
的函数是（ ）
A. 
B.
C. 
D.
（2）当
时，复数
在复平面上对应的点位于（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
（3）双曲线
的渐近线方程是（ ）
A. 
B.
C. 
D.
（4）一个圆锥的侧面积是其底面积的2倍，则该圆锥的母线与底面所成的角为（ ）
A. 
B.
C.
D.
（5）已知
，则下列不等关系中必定成立的是（ ）
A. 
，
B.
C.
D.
（6）在抛物线
上，横坐标为4的点到焦点的距离为5，则p的值为（ ）
A. 
B.
1 C.
2 D.
4
（7）已知a，b，c，d均为实数，有下列命题：
<1>若
，则
；
<2>若
，则
<3>若
，则
其中正确命题的个数是（ ）
A. 0 B. 1 C. 2 D. 3
（8）两个完全相同的长方体的长、宽、高分别为5cm，4cm，3cm，把它们重叠在一起组成一个新长方体，在这些新长方体中，最长的对角线的长度是（ ）
A. 
B.
C.
D.
（9）在100件产品中有6件次品，现从中任取3件产品，恰有1件次品的不同取法的种数是（ ）
A. 
B.
C.
D.
（10）期中考试以后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M:N为（ ）
A. 
B.
1 C.
D.
2
第II卷（非选择题共100分）
注意事项：
1. 第II卷共7页，用钢笔或圆珠笔直接答在试题卷中。
2. 答卷前将密封线内的项目填写清楚。
二. 填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。
（11）直线
（a为实常数）的倾斜角的大小是_________。
（12）
的值为____________。
（13）若
为函数
的反函数，则的值域是_______。
（14）若直线
与圆
没有公共点，则m，n满足的关系式为____________；以（m，n）为点P的坐标，过点P的一条直线与椭圆
的公共点有_________个。
三. 解答题：本大题共6小题，共84分。解答应写出文字说明，证明过程或演算步骤。
（15）（本小题满分13分）
解不等式
。
（16）（本小题满分13分）
在
中，a，b，c分别是
的对边长，已知a，b，c成等比数列，且
，求
的大小及
的值。
（17）（本小题满分15分）
如图，四棱锥
的底面是边长为1的正方形，SD垂直于底面ABCD，
。
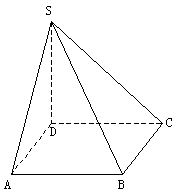
（I）求证
；
（II）求面ASD与面BSC所成二面角的大小；
（18）（本小题满分14分）
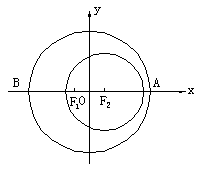
2003年10月15日9时，“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行。该轨道是以地球的中心
为一个焦点的椭圆。选取坐标系如图所示，椭圆中心在原点。近地点A距地面200km，远地点B距地面350km。已知地球半径R＝6371km。
（I）求飞船飞行的椭圆轨道的方程；
（II）飞船绕地球飞行了十四圈后，于16日5时59分返回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约
，问飞船巡天飞行的平均速度是多少km/s？（结果精确到1km/s）（注：km/s即千米/秒）
（19）（本小题满分15分）
某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元。该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低0.02元。根据市场调查，销售商一次订购量不会超过500件。
（I）设一次订购量为x件，服装的实际出厂单价为P元，写出函数
的表达式；
（II）当销售商一次订购了450件服装时，该服装厂获得的利润是多少元？
（服装厂售出一件服装的利润＝实际出厂单价－成本）
（20）（本小题满分14分）
下表给出一个“等差数阵”： 
| 4 | 7 | （ ） | （ ） | （ ） | …… |
| …… |
| 7 | 12 | （ ） | （ ） | （ ） | …… |
| …… |
| （ ） | （ ） | （ ） | （ ） | （ ） | …… |
| …… |
| （ ） | （ ） | （ ） | （ ） | （ ） | …… |
| …… |
| …… | …… | …… | …… | …… | …… | …… | …… |
|
|
|
|
|
| …… |
| …… |
| …… | …… | …… | …… | …… | …… | …… | …… |
其中每行、每列都是等差数列，
表示位于第i行第j列的数。
（I）写出
的值；
（II）写出的计算公式以及2008这个数在等差数阵中所在的一个位置。
【试题答案】
普通高等学校春季招生考试
数学试题（理工农医类）参考解答
一. 选择题：本大题主要考查基本知识和基本运算。每小题5分，满分50分。
（1）A （2）D （3）A （4）C （5）B
（6）C （7）D （8）C （9）A （10）B
二. 填空题：本大题主要考查基本知识和基本运算。每小题4分，满分16分。
（11）
（12）1
（13）
（14）
2
三. 解答题：本大题共6小题，共84分。解答应写出文字说明，证明过程或演算步骤。
（15）本小题主要考查不等式的解法等基本知识，考查运算能力和逻辑思维能力，满分13分。
解：原不等式的解集是下面不等式组(1)及(2)的解集的并集：
或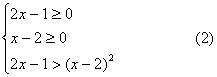
解不等式组(1)得解集
解不等式组(2)得解集
所以原不等式的解集为
（16）本小题主要考查解斜三角形等基本知识，考查逻辑思维能力、分析问题和解决问题的能力。满分13分。
解：（I）
成等比数列
又
在中，由余弦定理得
（II）解法一：在中，由正弦定理得
解法二：在中，由面积公式得
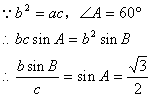
（17）本小题主要考查直线与平面的位置关系等基本知识，考查空间想象能力、逻辑思维能力和运算能力。满分15分。
（I）证法一：如图1
图1
底面ABCD是正方形
底面ABCD
DC是SC在平面ABCD上的射影
由三垂线定理得
证法二：如图1
底面ABCD是正方形
底面ABCD
，又
平面SDC
（II）解法一：
底面ABCD，且ABCD为正方形
可以把四棱锥补形为长方体
，如图2
面ASD与面BSC所成的二面角就是面
与面
所成的二面角，
又
为所求二面角的平面角
在
中，由勾股定理得
在
中，由勾股定理得
即面ASD与面BSC所成的二面角为
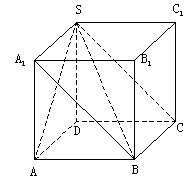
图2
解法二：如图3
过点S作直线
在面ASD上
底面ABCD为正方形
在面BSC上
为面ASD与面BSC的交线
为面ASD与面BSC所成二面角的平面角。
（以下同解法一）
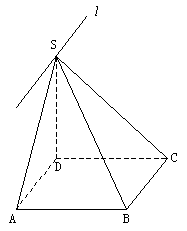
图3
（18）本小题主要考查椭圆等基本知识，考查分析问题和解决问题的能力。满分14分
解：（I）设椭圆的方程为
由题设条件得
解得
所以
所以椭圆的方程为
（注：由
得椭圆的方程为
，也是正确的。）
（II）从15日9时到16日6时共21个小时，合21×3600秒
减去开始的9分50秒，即9×60＋50＝590（秒），再减去最后多计的1分钟，共减去590＋60＝650（秒）
得飞船巡天飞行的时间是
（秒）
平均速度是
（千米/秒）
所以飞船巡天飞行的平均速度是8km/s。
（19）本小题主要考查函数的基本知识，考查应用数学知识分析问题和解决问题的能力。满分15分
解：（I）当
时，
当
时，
所以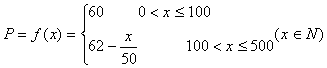
（II）设销售商的一次订购量为x件时，工厂获得的利润为L元，则
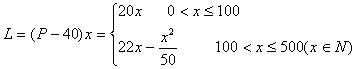
当
时，
因此，当销售商一次订购了450件服装时，该厂获利的利润是5850元。
（20）本小题主要考查等差数列等基本知识，考查逻辑思维能力、分析问题和解决问题的能力。满分14分
解：（I）
（II）该等差数阵的第一行是首项为4，公差为3的等差数列：
第二行是首项为7，公差为5的等差数列：
……
第i行是首项为
，公差为
的等差数列，因此
要找2008在该等差数阵中的位置，也就是要找正整数i，j，使得
所以
当
时，得
所以2008在等差数阵中的一个位置是第1行第669列。
| 年级 | 高中 | 学科 | 数学 | 版本 | 期数 | ||||||||
| 内容标题 | 2004年普通高等学校春季招生考试—数学（文史类）（北京卷） | ||||||||||||
| 分类索引号 | G.622.475 | 分类索引描述 | 统考试题与题解 | ||||||||||
| 主题词 | 2004年普通高等学校春季招生考试—数学（文史类）（北京卷） | 栏目名称 | 高考题库 | ||||||||||
| 供稿老师 | 审稿老师 | ||||||||||||
| 录入 | 许咏梅 | 一校 | 康纪云 | 二校 | 审核 | ||||||||