高三数学试卷（文科）抽样测试-高中三年级数学试题练习、期中期末试卷、测验题、复习资料-高中数学试卷-试卷下载

高三数学试卷（文科）抽样测试

学校　　　　　　　　　　　　班级　　　　　　　　　　　姓名　　　　　　　

题号

一

二

三

总分

分数

一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1、圆(x－1)²＋y²=1的圆心到直线y=x的距离是（　）

　 A、　　 B、　　 C、　　 D、1

2、函数的图象是（　　）

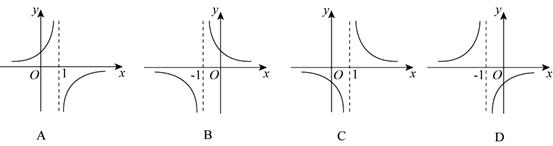
3、设a＞b＞0，则下列不等式成立的是（　　）

　 A、　　 B、　　 C、　　 D、

4、已知圆锥高为h，底面圆半径、锥高、母线长构成等比数列，则圆锥的侧面积是（　　）

　 A、　　 B、　　 C、　　 D、

5、等差数列{a _n}中，已知，a ₂＋a ₅=4，a _n=33，则n为（　）

　 A、48　　　B、49　　　C、50　　　D、51

6、双曲线经过坐标原点，焦点为F₁(0，1)，F₂(0，－5)，则其离心率是（　　）

　 A、3　　　B、2　　　C、　　 D、

7、将3种农作物都种植在如图的4块试验田里，每块种植一种农作物，要求相邻的试验田不能种植同一种作物，则不同的种植方法共有（　　）

　 A、6种　　　B、12种　　　C、18种　　　D、24种

8、关于函数f (x)=(x∈R且x≠0)，有下列三个结论：

①f (x)的值域为R；

②f (x)是区间(0，＋∞)上的增函数；

③对任意x∈R且x≠0，有f (－x)＋f (x)=0成立

　其中全部正确的结论是（　　）

　 A、①、②、③　　　B、①、③　　　C、①、②　　　D、②、③

二、填空题：本大题共6小题，每小题5分，共30分，把答案填在题中横线上

9、设集合A={－3，－2，－1，0，1，2，3}，映射f ：A→B把集合A中的元素k映射到B中的元素k ，则在影射f下，－2的象是　　　　；若集合B中每个元素都有原象，则集合B中的元素个数是　　　个。

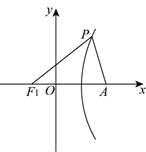
10、动点P(x，y)到定点F(1，0)的距离与到直线x=－1的距离相等，则动点P的轨迹方程式　　　　　　　；该曲线上的点与定点A(－1，0)距离的最小值是　　　　

11、设z∈C，且(1－i )z =2i ，则z=　　　　； z =　　　　

12、直线x＋y=0的倾斜角是　　　；它与直线的夹角是　　　　

13、已知m、n表示直线，a表示平面，给出下列两个命题：

　　①m⊥a，n∥a，则m⊥n；　　　 ②m⊥a，m⊥n，则n∥a

　　其中错误的一个命题是　　　　　　（填命题序号）；因为当　　　　　时，该结论不成立

14、设函数f (x)=2log₂(x＋1)－log₂x，则f (x)的定义域是　　　　；f (x)的最小值是　　　　

三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤

15、（本题满分12分）

　　解不等式：

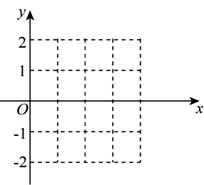16、（本题满分14分）

　　已知函数f (x)=2sin²x＋sin2x－1，x∈R

　　(Ⅰ)求f (x)的最小正周期及f (x)取得最大值时x的集合；

　　(Ⅱ)在给定的坐标系中画出函数f (x)在[0 ，π]上的图象

17、（本题满分14分）

　　已知数列{a _n}是等比数列，其前n项和是S_n，a₁＋2a₂=0，S₄－S₂=

　　 (Ⅰ)求数列{a _n}的通项公式

　　 (Ⅱ)求的值

　　 (Ⅲ)解关于n的不等式：

18、（本题满分14分）

　在长方体ABCD－A₁B₁C₁D₁中，已知AB=BC=1，BB₁=，连接BC₁，过B₁作B₁E⊥BC₁交CC₁于点E

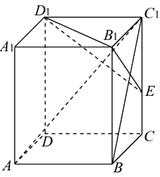(Ⅰ)求证：AC₁⊥平面B₁D₁E；

(Ⅱ)求三棱锥C₁－B₁D₁E₁的体积；

(Ⅲ)求二面角E－B₁D₁－C₁的平面角大小

19、（本题满分12分）

　　某企业2000年底共有员工2000人，当年的生产总值为1.6亿元，该企业规划从2001年起的10年内每年的总产值比上一年增加1000万元；同时为扩大企业规模，该企业平均每年将录用m(m＞50，m∈N)位新员工；经测算这10年内平均每年退休的员工为50人，设从2001年起的第x年（2001年为第1年）该企业的人均产值为y万元。

(1)填写下表：

2000年该企业的总产值（万元）	2000年该企业的员工总数（人）	从2001年起的第x年该企业的总产值（万元）	从2001年起的第x年该企业的员工总数（人）
16000	2000

(2)写出y与x之间的函数关系式y=f (x)，并注明定义域；

(3)要使该企业的人均产值在10年内每年都有增长，则每年录用新员工至多为多少人？

20、（本题满分14分）

　椭圆C₁：（a＞）的左、右焦点分别为F₁、F₂，右顶点为A，M为椭圆C₁上任意一点，且的最大值为4

(1)求实数a的值；

(2)设双曲线C₂以椭圆C₁的焦点为定点，顶点为焦点；在第一象限内任取双曲线C₂上一点P，试问是否存在常数λ(λ＞０)，使得∠PAF₁=λ∠PF₁A恒成立？证明你的结论。

『答案』

一、选择题

1、B　　　2、A　　　3、D　　　4、C　　　5、C　　　6、D　　　7、C　　　8、A

二、填空题

9、2 ；4　　　　　　　　　　　　10、y²=4x ；1 　　　　　　　　 11、－1＋i ；　

12、；　　　　　　　　　　　13、② ；nÌa　　　　　　　　　　 14、{x x＞0} ；2

三、解答题

15、

解：原不等式同解于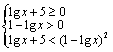 …………………………………………………………　４分

　……………………………………………………… 8分

所以原不等式的解集是 ……………………………………………………… 12分

16、

(1)解：f (x)=2sin²x＋sin2x－1= sin2x－(1－2sin²x)= sin2x－cos2x

　　　　　　 = …………………………………………………………………… 5分

所以f (x)的最小正周期是π ………………………………………………………………　6分

∵x∈R，所以，即时，f (x)的最大值为，即f (x)取得最大值时x的集合为 …………………………………………………………………　8分

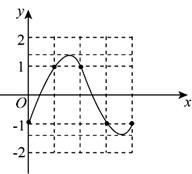(2)解：图象如下所示：

　　　　1、最大值

　　　　最小值 ………………………　10分

　　　　2、增区间，；

　　　　减区间 ………………………………　 12分

3、图象上的特殊点：(0，1)，，，，(π，－1) ……………………………　 14分

[注：图象上的特殊点错两个扣1分，最多扣2分]

17、

(1)解：设等比数列{a_n}的公比是q，

因为a₁＋2a₂=0，且a₁≠0，所以 ………………………………………………………　 3分

因为S₄－S₂=，所以，

将代入上式，解得：a₁=1 ……………………………………………………………………　 6分

所以，(n∈N) …………………………………………………………………　　7分

(2)解：因为{a_n}是等比数列，且 q ＜１，

所以　……………………………………………………………………………　　10分

(3)解：

显然当n是偶数时，此不等式不成立

当n是奇数时，

所以原不等式的解为n=1或n=3或n=5 ……………………………………………………………　 14分

18、

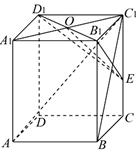(1)证明：连接A₁C₁交B₁D₁于点O

∵ABCD－A₁B₁C₁D₁是长方体

∴AA₁⊥平面A₁B₁C₁D₁，A₁C₁是AC₁在平面A₁B₁C₁D₁上的射影

∵AB=BC，∴A₁C₁⊥B₁D₁，

根据三垂线定理得：AC₁⊥B₁D₁；…………………………………　 3分

∵AB⊥平面BCC₁B₁，且BC₁⊥B₁E，

∴AC₁⊥B₁E

∵B₁D₁∩B₁E=B₁，

∴AC₁⊥平面B₁D₁E …………………………………………………………………………………　　5分

(2)解：在Rt△BB₁C₁中，

在Rt△EC₁B₁中，C₁E=B₁C₁·tg∠C₁B₁E=B₁C₁·ctg∠BC₁B₁=，……………………………　　 8分

∴ ……………………　　 10分

(3)解：连接OE，∵△B₁C₁E₁≌△D₁C₁E₁ ，　 ∴B₁E=D₁E

∵O是B₁D₁中点，　 ∴B₁D₁⊥OE，

∴∠C₁OE是二面角E―B₁D₁―C₁的平面角， ………………………………………………………　　 12分

在Rt△OC₁E中，∵OC₁= C₁E ，　 ∴∠C₁OE = 45^o

所以，二面角E―B₁D₁―C₁的平面角为45^o ………………………………………………………　　 14分

19、

(1)解：

2000年该企业的总产值（万元）	2000年该企业的员工总数（人）	从2001年起的第x年该企业的总产值（万元）	从2001年起的第x年该企业的员工总数（人）
16000	2000	16000＋1000x	2000＋(m－50)x