高三年级数学综合练习三
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第I卷1至2页。第Ⅱ卷3至8页。共150分。考试时间120分钟。
第I卷(选择题共50分)
注意事项:
1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用像皮擦干净后,再选涂其它答案,不能答在试题卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
参考公式:
三角函数的和差化积公式
![]()
![]()
![]()
![]()
正棱台、圆台的侧面积公式
![]()
其中c′、c分别表示上、下底面周长, l表示斜高或母线长
台体的体积公式
![]()
其中S′、S分别表示上、下底面积,h表示高
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)下列集合中表示空集的是
(A){0} (B)![]()
(C){x ctgx = 0} (D)![]()
(2)(理)![]() 的值是
的值是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(文)已知![]() ,
,![]() ,那么ctgθ的值等于
,那么ctgθ的值等于
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(3)已知![]() ,且f(-1)=0,那么
,且f(-1)=0,那么![]() 的值是
的值是
(A)0 (B)1
(C)-1 (D)![]()
(4)(理)已知点A,B的极坐标分别是![]() ,(8,
,(8,![]() ),那么线段AB的中点C的极坐标可以是
),那么线段AB的中点C的极坐标可以是
(A)(4,![]() ) (B)(4,
) (B)(4,![]() )
)
(C)(4,![]() ) (D)(4,
) (D)(4,![]() )
)
(文)若![]() ,
,![]() ,则A,B两点间的距离为
,则A,B两点间的距离为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(5)将一张坐标纸折叠一次,使得点(0,2)与(-2,0)重合,且点(2002,2003)与点(m,n)重合,则m-n 的值为
(A)1 (B)-1
(C)0 (D)-2
(6)已知直线a、b和平面M、N,且a⊥M,那么
(A)b∥M![]() b⊥a (B)b⊥a
b⊥a (B)b⊥a![]() b∥M
b∥M
(C)N⊥M![]() a∥N (D)
a∥N (D)![]()
(7)从不同品牌的4台快译通和不同品牌的5台录音笔中任意抽取3台,其中至少要有快译通知录音笔各1台,则不同的取法共有
(A)140种 (B)84种
(C)70种 (D)35种
(8)若复数z与它的共轭复数![]() 满足
满足![]() ,
,![]() ,则
,则![]() 的最大值是
的最大值是
(A)![]() (B)
(B)![]()
(C)![]() (C)2
(C)2
(9)若当P(m,n)为圆![]() 上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是
上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(10)已知![]() 是棱长为a的正方体,P是
是棱长为a的正方体,P是![]() 上的定点,Q是
上的定点,Q是![]() 上的动点,长为b(b是常数,0 < b < a)的线段EF在棱AB上滑动,那么四面体PQEF的体积是
上的动点,长为b(b是常数,0 < b < a)的线段EF在棱AB上滑动,那么四面体PQEF的体积是
(A)常量 (B)变量且有最大值
(C)变量且有最小值 (C)变量且有最大值也有最小值
第Ⅱ卷(非选择题共100分)
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
(11)已知椭圆![]() 与
与![]() 有相同的离心率e,那么m的值为___________.
有相同的离心率e,那么m的值为___________.
(12)设等差数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,则
,则![]() 的值是_________。
的值是_________。
(13)如图,直三棱柱![]() 中,P、Q分别是侧棱
中,P、Q分别是侧棱![]() 、
、![]() 上的点,且
上的点,且![]() ,则四棱锥
,则四棱锥![]() 的体积与多面体
的体积与多面体![]() 的体积的比值为________。
的体积的比值为________。
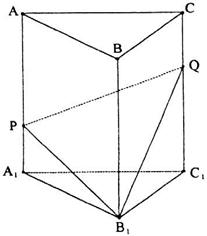
第(13)题图
(14)已知函数![]() ,若
,若![]() ,且
,且![]() ,那么
,那么![]() 的值是_______________。
的值是_______________。
三、解答题:本大题共6小题,共84分。解答应写出文字说明,证明过程或演算步骤。
(15)(本小题满分13分)
解关于x的不等式![]() (a>0,a≠1)。
(a>0,a≠1)。
(16)(本小题满分13分)
设函数![]() (x≠1,a>b)。
(x≠1,a>b)。
(I)求f(x)的反函数![]() ;
;
(Ⅱ)判断![]() 在(-b,+∞)上的单调性并用函数单调性定义加以证明。
在(-b,+∞)上的单调性并用函数单调性定义加以证明。
(17)(本小题满分14分)
某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用为每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每超过1元,租不出去的自行车就增加3辆。
为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费后的所得)。
(I)求函数y = f(x)的解析式及其定义域;
(Ⅱ)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
(必要时可参考以下数据:![]() )。
)。
(18)(本小题满分14分)
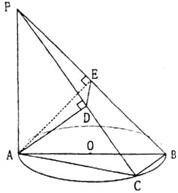
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上的一点,若A在PC,PB上的射影为D、E。
(Ⅰ)求证:AD⊥平面PBC;
(Ⅱ)若PA=AB=2,∠BPC=θ,试用tgθ表示△ADE的面积,当tgθ取何值时,△ADE面积最大,最大面积是多少?
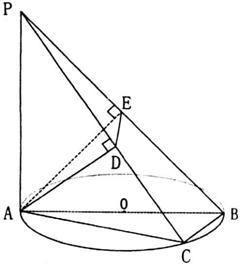
第(18)题图
(19)(本小题满分15分)
已知抛物线方程为![]() (p >0),直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3。
(p >0),直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3。
(Ⅰ)求p的值;
(Ⅱ)是否存在点M,使过点M的斜率不为零的任意直线与抛物线交于P、Q两点,并且以PQ为直径的圆恰过抛物线的顶点?若存在,求出M点的坐标;若不存在,请说明理由。
(20)(本小题满分15分)
若![]() 和
和![]() 分别表示数列
分别表示数列![]() 和
和![]() 的前n项的和,对任意正整数n,
的前n项的和,对任意正整数n,![]() ,
,![]() 。
。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)在平面直角坐标系内,直线![]() 的斜率为
的斜率为![]() ,且与曲线
,且与曲线![]() 有且仅有一个交点,与y轴交于点
有且仅有一个交点,与y轴交于点![]() ,记
,记![]() ,求
,求![]() ;
;
(Ⅲ)若![]() ,求证:
,求证:![]() 。
。
高三年级综合练习三
数学参考答案及评分标准
一、(1)D(2)B(3)A(4)C(5)B(6)A(7)C(8)A(9)D(10)A
二、(11)4或1(12)0(13)![]() (14)0
(14)0
三、(15)解:原不等式即![]() 。…………………1分
。…………………1分
①当a>1时,原不等式等价于
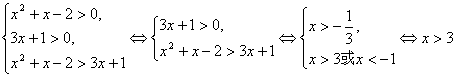 。……6分
。……6分
②当0<a<1时,原不等式等价于
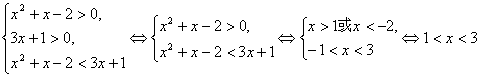 。……11分
。……11分
∴当a>1时,原不等式的解集为{xx>3},
当0<a<1时,原不等式的解集为{x1<x<3}。……………………13分
(16)解:(I)设![]()
则有y-xy=bx-a。
(b+y)x=y+a
∴![]() ,……………………5分
,……………………5分
即![]() ,………………6分
,………………6分
(Ⅱ)![]() 在(-b,+∞)是单调递减函数。证明如下:
在(-b,+∞)是单调递减函数。证明如下:
任取![]() ,
,![]() ,且
,且![]() 。
。
![]()
![]() 。……………………11分
。……………………11分
∵a>b,∴a-b>0。
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() 。
。
∴![]() ,即
,即![]() 。
。
故![]() 在
在![]() 上是单调递减函数。…………………………13分
上是单调递减函数。…………………………13分
(17)解:(I)当x≤6时,
y=50x-115。………………2分
令50x-115>0。解得x>2.3。
∵x∈N,∴x≥3。
∴3≤x≤6,x∈N。……………………3分
当x>6时,
y=[50-3(x-6)]x-115。…………………………5分
令[50-3(x-6)]x-115>0,
有![]() 。
。
上述不等式的整数解为![]() 。
。
∴6<x≤20。(x∈N)……………………6分
故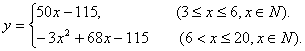
定义域为3≤x≤20,x∈N…………………………8分
(Ⅱ)对于y=50x-115(3≤x≤6,x∈N)。显然当
x=6时,![]() (元)……………………9分
(元)……………………9分
对于![]()
(6<x≤20,x∈N)。………………………………11分
当x=11时,![]() (元)。…………………………13分
(元)。…………………………13分
综上所述当每辆自行车日租金定在11元时,才能使一日的净收入最高。……………………14分
(18)(I)证明:∵PA⊥平面ABC,∴PA⊥BC,
又AB是圆O直径,C是圆周上一点,
∴AC⊥BC。
∵![]() ,
,
∴BC⊥平面PAC。……………………4分
又![]() 平面PAC,
平面PAC,
∴BC⊥AD。
由已知AD⊥PC,
又![]() ,
,
∴AD⊥平面PBC。……………………7分
(Ⅱ)解:在Rt△PAB中,PA=AB=2,
∵E是A点在PB上的射影,
∴![]() 。……………………8分
。……………………8分
由(I)AD⊥平面PBC,
AE⊥PB于E,
∴PB⊥ED,则![]() 。……………………10分
。……………………10分
在Rt△ADE中,![]() 。……………………11分
。……………………11分
![]()
![]() 。……………………………13分
。……………………………13分
当且仅当![]() ,即
,即![]() 时
时![]() 最大,最大面积是
最大,最大面积是![]() 。……………………14分
。……………………14分
(19)解:(I)设l与抛物线交于![]() ,
,![]() 则AB=3。
则AB=3。
由距离公式![]()
![]()
![]()
则有![]() .……………………3分
.……………………3分
由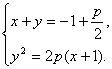 消去x,得
消去x,得
![]() 。………………………………4分
。………………………………4分
![]() 。
。
∴![]() ,
,![]() 。……………………5分
。……………………5分
从而![]() ,
,
即![]() 。……………………6分
。……………………6分
由于p>0,
解得![]() 。…………………………7分
。…………………………7分
(Ⅱ)设过M点的直线为![]() ,
,![]() ,
,![]()
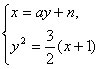 。消去x,得
。消去x,得
![]() 。……………………9分
。……………………9分
![]() 。
。
![]() ,
,![]() 。……………………10分
。……………………10分
由题意,![]()
即![]()
![]()
![]()
∴![]() 。
。
∴n=-1,![]() 。……………………12分
。……………………12分
当n=-1时,由题设知a≠0,故△>0,此时动直线为x=ay-1,过定点(-1,0)。而(-1,0)是抛物线![]() 的顶点。不合题意。
的顶点。不合题意。
当![]() 时,△>0,此时动直线为
时,△>0,此时动直线为![]() ,过定点
,过定点![]() 。…………………14分
。…………………14分
故存在点![]() 满足条件。……………………15分
满足条件。……………………15分
(20)(I)解法(一)由已知![]() 。
。
当n=1时,![]() 。……………………1分
。……………………1分
当n≥2时,![]()
![]()
由于![]() 。
。
∴![]() 。……………………4分
。……………………4分
由于![]() 适合上式,
适合上式,
∴![]() 。……………………5分
。……………………5分
解法(二)由于![]() ,则
,则![]() 为等差数列,
为等差数列,![]() 。
。
![]() 。………………1分
。………………1分
∴![]() 。……………………2分
。……………………2分
当n=1时,![]() ,……………………3分
,……………………3分
当n≥2时,![]()
=-6n-2。……………………4分
由于![]() 适合上式,∴
适合上式,∴![]() 。……………………5分
。……………………5分
解:(Ⅱ)设![]() 的方程为
的方程为![]() 。
。
由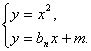 消去y,得
消去y,得
![]() 。……………………7分
。……………………7分
∵直线![]() 与曲线只有一个交点,
与曲线只有一个交点,
∴△=0,即![]() 。
。
∴![]() 。
。
则![]() 。…………………………8分
。…………………………8分
从而![]()
![]()
![]()
=6n+5-(2n+7)
=4n-2。
∴![]() 。…………………………10分
。…………………………10分
(Ⅲ)∵![]()
![]() 。…………………………12分
。…………………………12分
∴![]()
![]()
![]() 。……………………14分
。……………………14分
∴![]() 。……………………15分
。……………………15分