高三期末数学测试试题
一.选择题(本大题共12个小题,毎小题5分,共60分.毎小题只有一个正确答案)
1.已知复数z1=1-i,z2=![]() +i,则z=
+i,则z=![]() 在复平面内对应点位于( )
在复平面内对应点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若向量![]() 则
则![]() 一定满足( )
A.
一定满足( )
A.![]() 的夹角等于
的夹角等于![]() B.
B.![]() ⊥
⊥![]()
C.![]() ∥
∥![]() D.
D.![]() ⊥
⊥![]()
3.函数![]() 是奇函数的充要条件为( )
是奇函数的充要条件为( )
A.b=0 B.a=0 C.ab=0 D.a2+b2=0
4.一个凸多面体的顶点数为20,棱数为30。则它的各面多边形的内角总和为( )
A、2160° B、5400° C、6480° D、7200°
5.若动点P、Q是椭圆9x2+16y2=144上的两点,O是其中心,若![]() ,则中心O到线段PQ的距离OH必为( )
,则中心O到线段PQ的距离OH必为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6.对函数f(x)=ax2+bx+c(a≠0)作x=h(t)的代换,则不改变函数f(x)值域的代换是( )
A、h(t)=10t B、h(t)=t2 C、h(t)=sint D、h(t)=log2t
7.设A是原命题,![]() 是A的否命题.若B是
是A的否命题.若B是![]() 的必要非充分条件,那么A是
的必要非充分条件,那么A是![]() 的( )
的( )
A、充分非必要条件B.必要非充分条件C.充要条件D.非充分非必要条件
8.如果一个平面与一个正方体的十二条棱所在的直线都成相等的角,记作θ,那么sinθ的值为( )
A、![]() B、
B、![]() C、
C、![]() D、1
D、1
9.设F1,F2是双曲线![]() 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且![]() ,则
,则![]() 的值等于( )
的值等于( )
A.2 B.![]() C.4 D.8
C.4 D.8
10.已知数列![]() 的通项公式
的通项公式![]() ,设其前
,设其前![]() 项和为
项和为![]() ,则使
,则使![]() 成立的自然数
成立的自然数![]() ( )
( )
A.有最小值63 B.有最大值63
C.有最小值31 D.有最大值31
11.已知f(x)=x2+ax-3a-9,对任意x![]() R,恒有f(x)
R,恒有f(x)![]() 0,则f(1)的值等于( )
0,则f(1)的值等于( )
(A)3 (B)4 (C)5 (D)6
12.定义运算a*b为:a*b=![]() ,例如,1*2=1,则1*2x的取值范围是( )
,例如,1*2=1,则1*2x的取值范围是( )
A、(0,1) B、(-∞,1] C、(0,1] D、[1,+∞)
二.填空题(毎小题4分,共16分)
13.如果不等式![]() 和
和![]() 同时成立, 则
同时成立, 则![]() 的取值范围是 .
的取值范围是 .
14.已知数列![]() 满足:
满足:![]() ,则使
,则使![]() 成立的
成立的![]() 的值是 .
的值是 .
15.已知x、y满足约束条件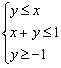 ,则z=2x+y的最大值是 .
,则z=2x+y的最大值是 .
16.有一组数据:![]() ,它们的算术平均值为10,若去掉其中最大的
,它们的算术平均值为10,若去掉其中最大的![]() ,余下数据的算术平均值为9;若去掉其中最小的
,余下数据的算术平均值为9;若去掉其中最小的![]() ,余下数据的算术平均值为11。 则
,余下数据的算术平均值为11。 则![]() 关于n的表达式为___________;
关于n的表达式为___________;![]() 关于n的表达式为___________。
关于n的表达式为___________。
三.解答题(本大题共6个小题,共74分要有必要的步骤) 17.( 本题满分12分)已知函数
![]()
(1)求![]() 的最小正周期;
的最小正周期;
(2)求![]() 的单调递减区间;
的单调递减区间;
(3)(理做文不做)函数![]() 的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
18.(本题满分12分)如图,PA⊥矩形ABCD所在平面,PA=AD=a,M,N分别是AB,PC的中点。
(1)求证:平面MND⊥平面PCD;
(2)若AB=![]() ,求二面角N-MD-C的大小。
,求二面角N-MD-C的大小。
19.(本题满分12分)已知数列![]() 成等差数列,
成等差数列,![]() 表示它的前
表示它的前![]() 项和,
项和,
且![]() ,
,
![]() .
.
⑴求数列![]() 的通项公式
的通项公式![]() ;
;
⑵数列![]() 中,从第几项开始(含此项)以后各项均为正数?
中,从第几项开始(含此项)以后各项均为正数?
20.(本小题满分12分)
经市场调查分析知,某地明年从年初开始的前n个月,对某种商品需求总量f(n)(万件)近似地满足下列关系:![]() (n=1,2,3,…,12)
(n=1,2,3,…,12)
(1)写出明年第n个月这种商品需求量g(n)(万件)与月份n的函数关系式,并求出哪几个月的需求量超过1.4万件;
(2)若计划每月该商品的市场投放量都是p万件,并且要保证每月都满足市场需求,则p至少为多少万件?
21.(本题满分12分)已知![]() =(x,0),
=(x,0),![]() =(1,y),
=(1,y),![]()
(1)求点P(x,y)的轨迹C的方程;
(2)若直线![]() :y=kx+m(km≠0)与曲线C交于A、B两点,已知D(0,-1),且有AD=BD,试求m的取值范围。
:y=kx+m(km≠0)与曲线C交于A、B两点,已知D(0,-1),且有AD=BD,试求m的取值范围。
22.(本题满分14分)借助计算机(器)作分段函数时,分段函数的表示可利用“函数”
![]() ,例如要表示分段函数
,例如要表示分段函数![]() ,可将g(x)表示为
,可将g(x)表示为![]()
设![]() ,
,
(1) 请将函数![]() 写成分段函数的形式;
写成分段函数的形式;
(2) 填写下表并画出函数![]() 的大致图像;(见答案卷)
的大致图像;(见答案卷)
(3) 设![]() ,是否存在实数
,是否存在实数![]() ,使
,使![]() 为奇函数?若存在,试求出
为奇函数?若存在,试求出![]() 的所有取值;若不存在,请说明理由。
的所有取值;若不存在,请说明理由。
(2)
|
| …… | -2 | -1 | 0 | 1 | 2 | 3 | …… |
| y | …… |
|
|
|
|
|
| …… |
期末数学参考答案
一.选择题
D B D C C D B B A A B C
二.填空题
13.![]() 14。21
15. 3 16. 11-n;n+9
14。21
15. 3 16. 11-n;n+9
三.解答题
⒘(1)由![]() 由
由
![]() ……2分
……2分
![]() ……6分
……6分
函数![]() 的最小正周期T=
的最小正周期T=![]() ……7分(2)由
……7分(2)由![]()
∴![]() 的单调递减区间是
的单调递减区间是![]()
![]() .
……10分
.
……10分
(3)![]() ,
,
∴奇函数![]() 的图象左移
的图象左移![]() 即得到
即得到![]() 的图象,
的图象,
故函数![]() 的图象右移
的图象右移![]() 个单位后对应的函数成为奇函数.
……12分
个单位后对应的函数成为奇函数.
……12分
(注:第Ⅲ问答案不唯一)
18. (1)∵M、N分别是AB、PC的中点,可得![]()
由于![]() ,………2分
,………2分
及![]() ,…4分
,…4分
∴MN⊥CD,又MN⊥DP, ∴MN⊥平面PCD, ∴平面MND⊥平面PCD.………6分
(2)底面的法向量为![]() ,设平面MN的法向量为
,设平面MN的法向量为![]() ,…7分
,…7分
![]()
![]() ,∴
,∴![]() .
.
![]()
![]() ,∴
,∴![]() .
.
∴![]() ,………………………………………………………9分
,………………………………………………………9分
∴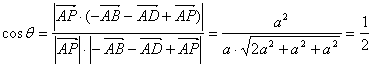 ,…………11分
,…………11分
∴二面角N-MD-C的大小为60°.………………………………………………12分
19(本小题满分12分)
⑴设数列![]() 的公差为
的公差为![]() ,由已知
,由已知
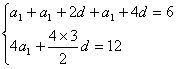
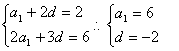 …… 4分
…… 4分
![]() ………………………………………………6分
………………………………………………6分
⑵![]() ……………………………7分
……………………………7分
解不等式![]() ,得
,得![]() …………………………… 8分
…………………………… 8分
∵![]() ,∴
,∴![]()
∴![]() ,或
,或![]() ………………………………………………………… 11分
………………………………………………………… 11分
故从第8项开始以后各项均为正数. …………………………………………12分
20. (本题满分12分)
解:(Ⅰ)当n=1时,![]() ;……………………2分
;……………………2分
当![]() 时,
时,
![]()
(经检验对n=1也成立)
∴![]() ………………………………5分
………………………………5分
解不等式![]() 得5<n<7
得5<n<7
∵![]() ,∴n=6。
,∴n=6。
即第6个月的需求量超过1.4万件。………………………………7分
(Ⅱ)由题设可知,对于n=1,2,…,12恒有:![]() ,
,
即![]() …………………………………………9分
…………………………………………9分
![]()
当且仅当n=8时,![]()
∴每月至少投放1.14万件。…………………………………………12分
21解:(1)![]()
![]() ……………………2分
……………………2分
∵![]() ∴
∴![]() =0
=0
∴![]() 得
得![]() …………4分
…………4分
∴P点的轨迹方程为![]() ………………………………………6分
………………………………………6分
(2)考虑方程组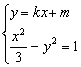 消去y,得(1-3k2)x2-6kmx-3m2-3=0(*)
消去y,得(1-3k2)x2-6kmx-3m2-3=0(*)
显然1-3k2≠0 △=(6km)2-4(-3m2-3)=12(m2+1)-3k2>0…………7分
设x1,x2为方程*的两根,则![]()
![]()
![]()
故AB中点M的坐标为(![]() ,
,![]() )
)
∴线段AB的垂直平分线方程为:![]()
将D(0,-1)坐标代入,化简得:4m=3k2-1
故m、k满足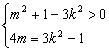 ,消去k2得:m2-4m>0
,消去k2得:m2-4m>0
解得:m<0或m>4………………………………………………………………10分
又∵4m=3k2-1>-1 ∴m>-![]() ……………………………………………11分
……………………………………………11分
故m![]() .………………………………………………………12分
.………………………………………………………12分
22,解:(1)![]()
![]() ,…………………………………………………2分
,…………………………………………………2分
(2)略. …………………………………………………………………………4分
(3)设存在实数k,使![]() 为奇函数,则必有
为奇函数,则必有![]() … 5分
… 5分
①当![]() 时,由
时,由![]() 得,
得,![]() .
.
②当![]() 时,由
时,由![]() 得
得![]() (舍),
(舍), ![]() ……………8分
……………8分
证明:(i)当![]() 时,有
时,有![]()
设a为任意实数,当![]() 时,
时,![]()
当![]() 时,显然有
时,显然有![]() , 当
, 当![]() 时,
时,![]()
所以,对任意实数a都有![]() ,即当
,即当![]() 时
时![]() 是奇函数……………10分
是奇函数……………10分
(ii)当![]() 时,
时,![]() ,
,![]()
所以当![]() 时,
时,![]() 不是奇函数.…………………………………………………12分
不是奇函数.…………………………………………………12分
(iii)当![]() 时,
时,![]() 也不是奇函数………………………………………………14分.
也不是奇函数………………………………………………14分.
注:解(3)时若直接给出当![]() 时,
时,![]() 是奇函数然后证明得10分若在指出
是奇函数然后证明得10分若在指出![]() 时,
时,![]()
![]() 不是奇函数得11分.
不是奇函数得11分.