高三上学期期中测试数学试题
数 学 试 卷
第Ⅰ卷(共60分)
一、选择题 (每小题5分，共60分)
1．若f(cosx)=
,x∈［0，π］，则f(－
)等于 （ ）
A．cos
B．
C．
D．
2．设集合A={1，2}，则从A到A的映射f 中满足f[f(x)]=f(x)的映射的个数 （ ）
A．1 B．2 C．3 D．4
3．设函数, f(x)= 
, x
4,则f(
)的值为 （ ）
f(x+3) x<4
A．
B．
C．
D．
4．已知a、b、c常数，且
的值是（
）
A．
B．
C．
D．6
5．函数y=f(x+1)与函数y=f
的图像关于 （ ）
A．y=x对称 B．y=x+1对称 C．y=x－1对称 D．y=－x对称
6．已知函数f(x)=log2（ｘ2－ａｘ＋3ａ）在区间［2，＋∞］上是增函数，则实数a的取
值范围是 （ ）
A．(－∞，4) B．[－4，4]
C．（－∞，－4）∪［2，＋∞］ D．［－4，4］
7．若函数
的值域是
，则它的定义域是 （ ）
A．
B．（0，2） C．（0，4） D．（2，4）
8．已知函数
满足
且
时，
则
与
的图象的交点的个数为 （ ）
A．3个 B．4个 C．5个 D．6个
9．已知直线x=1为函数y=f(2x)图象的一条对称轴，那么函数y=f(3－2x)的图象 （ ）
A．关于直线x=对称 B．关于直线x=－对称
C．关于直线x=对称 D．关于直线x=－对称
10．已知定义在R上的函数f(x)满足f(x－2)= f(x+2)，f(2+x)= f(2－x)，且f(x)不恒为零，
则f(x) （ ）
A． 是奇函数不是偶函数，不是周期函数
B．是偶函数不是奇函数，是周期函数
C．是偶函数不是奇函数，不是周期函数
D．不是奇函数不是偶函数，但是周期函数
11．设f(x)=
且f(x0)=17，则f
= （ ）
A．289 B．－288 C．－
D．－
12．若
=0，则A=x－y的最小值与最大值分别为 （ ）
A．－1,2 B．－
,1 C．－1, D． －,
二、填空题：（每小题4分，共16分）
13．设 a>b>0,a+b=1, 且x=log
b，y=log
a,z=log
a,则x,y,z的从大到小依次是________
14．a=－b是“
互共轭复数”的（ ）条件
15．f(x)=
+2ax－2a－1 在[0，1]上的最小值为0，则a的取值范围是_________
_
16．已知方程（x2－2x+m）(x2－2x+n)=0的四个根组成一个首项为1/4的等差数列，则
=____________
三、解答题：（共74分）
17．（本题12分）已知函数f(x)是函数
的反函数，函数g(x)的图像与
y=
关于直线y=-x成轴对称图形，记F(x)=f(x)+g(x),求函数F(x)的解析式及定义
域
18．（本题12分）已知函数f(x)=log
（1）求f(x)的定义域
（2）当a>0 时， 求使f(x)>0的所有x的值
19．（本题12分）设函数f(x)=
－ln
（1）求f(x)的单调区间
（2）若当x
[
]时，不等式f(x)<m恒成立，求实数m的取值范围.
20．（本题12分） 某地区地理环境偏僻，严重制约着经济的发展，某种土特产只能在本
地区销售，该地区政府每年投资x万元，所获利润为p=
万元。
为顺应开发大西北的宏伟决策，该地区政府在制定经济发展十年规划时，拟开发这种
土特产品，而开发前后用于该项目投资的专项财政拨款每年都是60万元。若开发该产
品，必须在前五年中，每年从60万元专款中拿出30万元投资一条公路，且5年可以
修通。公路修通后该产品可以在异地销售，每年投资x万元，可获利润
Q=
万元。问从十年的总利润来看，该项目是否有投资
的价值。
21．（本题12分）设0<a<1, 函数f(x)=log
,g(x)=1+ log
,设f(x)和g（x）
的定义域的公共部分为D，当[m,n]
D时，f(x)在[m,n](m<n)上的值域是[g(n),g(m)],
求a的取值范围。
22．（本题14分）已知集合是满足下列性质的函数f(x)的全体：
存在非零常数T, 对任意XR,有f(x+T)=Tf(x)成立
（1）函数f(x)=x是否属于集合M？说明理由
（2）设函数
的图象与y=x的图象有公共点，证明f(x)=
M
（3）若f(x)=sinkxM,求k的取值范围。
高三上学期期中测试
数学试题参考答案
1.B 2.C 3.D 4.D 5.B 6.B 7.B 8.B 9.A 10.B 11.C 12.B
13. x>y>z 14.既不充分也不必要 15. a
－1
16. 
17. F(x)=lg
+
－1 x(－1,1)
18. (1)a>0时，x>
,a=0,x
R;a<0, x<
(2)a>0 x(a+1－
, a+1+)
19．（1）x
由f
>0得（－2,－1 ），（0，+
）为
增区间，－1<x<0,x<－2 减区间
（1）在[]时，f(x)的最大值为
,所以，m>
20．解：若按原来投资环境不变，易知十年总利润的最大值为W=10P
=100万元；若对
该产品进行开发，易知前五年总利润M=5 P=5
万元，设后五年x万元
用于本地投资，60-x万元用于异地销售投资，则这五年的总利润
N=
，其
最大值为4500万元，所以这十年总利润的最大值为 
万元，这远远大于
原来的100万元，故极具开发价值。
21．D=（－3,1）
，又因为f(x)= log在（－3,1）为减函数。有：f(m)=g(m)、f(n)=g(n),
即m,n是方程=a(x+3)的两个根 ，且－3<m<n<1,所以有
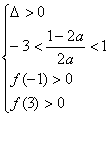
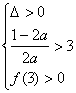
解之得
22．（1）f(x+T)=x+T=Tx 不能恒成立，所以不属于M
（2）
，所以存在T,使
，
属于M
（3）sink(x+T)=Tsinkx 当k=0时，等式成立,由等式可知T=1或－1，当T=1时，
k=－2mπ, 当T=－1时, k=－(2m+1)π(mZ),所以k=nπ(nZ)