高中学生学科素质训练
高三数学测试题—直线与平面（10）
一、选择题（本题每小题5分，共50分）
1．直线c、d与异面直线a、b都相交，则直线a、b、c、d可确定平面的个数是 （ ）
A．2 B．3 C．3或4 D．2或3
2．下列命题中正确的是 （ ）
A．过平面外一点作该平面的垂面有且只有一个
B．过直线外一点作该直线的平行平面有且只有一个
C．过直线外一点作该直线的垂线有且只有一条
D．过平面外的一条斜线作该平面的垂面有且只有一个
3．如果命题“若
∥z，则
”不成立，那么字母x、y、z在空间所表示的几何
图形一定是 （ ）
A．x、y、z都是直线 B．x、y、z都是平面
C．x、y是直线，z是平面 D．x、z是平面，y是直线
4．设A表示点a、b、c表示三条互不重合的直线，α、β表示两个不同的平面，那么下列
命题的逆命题不能成立的是 （ ）
A．a⊥α，若b⊥α，则a∥b
B．a⊥α，若a⊥β，则α∥β
C．
内的射影，若a⊥c则a⊥b
D．a⊥α,若b∥α，c∥a，则a⊥b, c⊥b
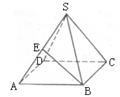
5．如图，正四棱锥的各棱长相等，E是SA的中点，则异面直线BE与SC所成的角是
|
A．
B．
C．60° D．
6．已知AB是异面直线a、b的公垂线段，AB=2，a与b成30°，在直线a上取AP=4，则
点P到直线b的距离是 （ ）
A．
B．2
C．
D．
7．正四面体棱长为a，过其一条棱的截面面积的最小值是 （ ）
A．
B．
C．
D．
8．二面角
的平面角为120°，在α内，AB⊥l于B，AB=2，在β内，CD⊥l于D，
CD=3，BD=1，M是棱l上的一个动点，则AM+CM的最小值是 （ ）
A．2 B．2
C．
D．
9．在空间四边形中，若AB=CD，BC=AD，AC=BD，则∠BAC、∠CAD、∠DAB的和的大
小为 （ ）
A．90° B．在区间（0，90°]
C．180° D．在区间（90°，180°）
10．等边△ABC边长是1，以BC边上的高AD为轴折成60°和二面角，则此时点A到BC
的距离是 （ ）
A．
B．
C．
D．
二、填空题（本题11—14小题每小题4分，15—16小题每小题5分，共26分）
11．ABCD—A1B1C1D1为正方体，其中二面角B—AC1—C的大小是 .
12．长方形ABCD与长方形CDEF所在二平面垂直，设AF与平面BD所成的角为α，AF
与CD两异面直线的角为β，且AB、BC、CF的长分别为4、3、2则cosα·cosβ=
.
13．正三棱锥的侧面与底面所成的二面角为
，则它的侧棱与底面所成的角为
.
14．棱长为a的正三棱柱ABC—A1B1C1中，已知M为A1B1的中点，则M到BC的距离是
.
15．已知正方形ABCD，E、F分别为AD、BC中点，AC交EF于O，现沿AC折成直二面
角，则折起后∠EOF的度数为 .
16．在棱长均为a的平行六面体ABCD—A1B1C1D1中，各表面四边形的锐角均为60°，则
二面角A1—AD—C（锐角）的余弦值为 .
三、解答题
17．（本题满分12分）
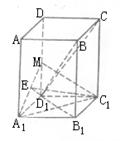
长方体ABCD—A1B1C1D1中，M、N分别为棱AB和对角线A1C的中点.
（1）求证：MN⊥AB；
（2）若MN是异面直线AB、A1C的公垂线，求二面角A1—DC—A的度数.
18．（本题满分12分）
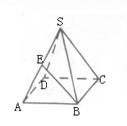
已知三棱锥P—ABC的底面是边长为a的正三角形，PC⊥底面ABC，PC=a，O、E分别为棱AC、PA中点.
（1）求证：平面EBO⊥平面ABC；
（2）求点E到平面PBC的距离.
19．（本题满分12分）
已知正四棱柱ABCD—A1B1C1D1，底面边长为3，侧棱长为4，连CD1，作C1M⊥CD1，交DD1于M.
（1）求证：BD1⊥平面A1C1M；
（2）求二面角C1—A1M—D1的大小.
20．（本题满分12分）
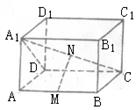
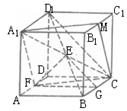
已知直四棱柱ABCD—A1B1C1D1底面是矩形,又A1A=AB，E、F分别是BD1和AD中点.
（1）求异面直线CD1、EF所成的角；
（2）证明EF是异面直线AD和BD1的公垂线；
（3）若M为B1C1中点，求证：平面A1FCM⊥平面BCD1.
21．（本题满分12分）
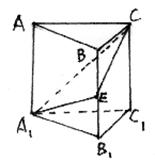
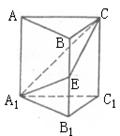
如图，在正三棱柱ABC—A1B1C1中，E∈BB1，截面A1EC⊥侧面AC1.
（1）求证：BE=EB1；
（2）若AA1=A1B1，求平面A1EC和平面A1B1C1所成二面角（锐角）的度数.
|
22．（本题满分14分）
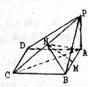
已知PA⊥矩形ABCD所在平面，M、N分别是AB、PC中点.
（1）求证：MN⊥AB；
（2）设平面PDC和平面ABCD所成的二面角为锐角θ，问能否确定θ，使得直线MN为异面直线AB与PC的公垂线，若能，求出对应的θ值；若不能，说明理由.
高三数学测试题参考答案
十、直线与平面
一、选择题
1．C 2．D 3．C 4．D 5．B 6．A 7．B 8．C 9．C 10．A
二、填空题
11．60°； 12．
； 13．； 14．
； 15．120°； 16．
|
17．（1）证明∵ABCD—A1B1C1D1为长方体，∴ACC1A1为矩形.
BDD1B1为矩形，∵N为A1C中点，∴AN=
又M为AB中点，∴MN⊥AB.
|
即A1A=BC=AD，∴∠A1DA=45°.
18．（1）证：∵E、O分别为AP、AC中点，∴OE∥PC，∵PC⊥平面ABC，
∴OE⊥平面ABC，∵OE
面EOB，∴平面EBO⊥平面ABC.
（2）解：∵OE∥PC，∴OE∥平面PBC，则点E到平面PBC的距离
等于点O到平面PBC的距离.作OD⊥BC于D，∵PC⊥OD，
∴OD⊥平面PBC，即OD为点O到平面PBC的垂线段.∵△ABC为正三角形,
，
|
19．（1）证：∵ABCD—A1B1C1D1为正四棱柱，∴BB1⊥A1B1C1D1，且B1D1⊥A1C1，
∴BD1⊥A1C1，又∵BC⊥平面C1CDD1，CD1为BD1在平面C1CDD1上的射影，
∵CD1⊥C1M，∴BD1⊥C1M，∴BD1⊥A1C1M.
（2）解：∵C1D1⊥平面A1D1M，作D1E⊥MA1于E，连C1E，则∠C1ED1为二面角C1—A1M—D1的
平面角.∵C1C=4，C1D1=3，∴CD1=5，∵MC1⊥CD1，设∠C1MD1=α，则
|
二面角C1—A1M—D1的大小为
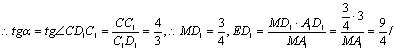
20．（1）解：取BC的中点G，连EG，则EG∥D1C，∴∠GEF为异面直线CD1
与EF所成的角.设AB=AA1=a,
∵D1F=
∴EF⊥BD1，
∵BC⊥平面CDD1C1，∴BC⊥CD1，∴BC⊥EG，又BC⊥FG，
∴BC⊥平面EFG，BC⊥EF，∴EF⊥平面BCD1，EF⊥EG，∠GEF=90°.
（2）证：由（1）知EF⊥BC，∴EF⊥AD，又EF⊥BD1，∴EF是异面直线BD1与AD的公垂线.
（3）证：显然BCD1A1为 ，∵E为BD1中点，∴E也是A1C的中点，即EF平面A1FCM，∵EF⊥平面BCD1，∴平面A1FCM⊥平面BCD1.
21．（1）证：在截面A1EC内，过E作EG⊥A1C，G为垂足，∵截面A1EC⊥侧面AC1，
|
∵面ABC⊥侧面AC1，∴BF⊥侧面AC1，则BF∥EG，B、E、F、G共面，
∵BE∥侧面AC1，∴BE∥FG，四边形BEGF为平行四边形，BE=FG，
∵AF=FC，∴A1G=GC，∴FG∥
AA1=BB1，即BE=BB1，∴BE=EB1.
（2）解：设AA1=A1B1=a，平面A1EC与平面A1B1C1所成角为θ，则有
|
22．（1）证：∵PB⊥矩形ABCD，∴PB⊥BC，PA⊥AC，即△PBC与△PAC都是Rt△.
∵N为PC中点，∴AN=
PC=BN，∵M为AB中点，∴MN⊥AB
（2）解连PD，∵AD⊥DC，∴PD⊥CD，∠PDA为平面PDC与平面ABC所成二面角的平面角，
∠PDA=θ. 设AB=a，PA=AD=b. 则PM=
即PM=CM，∵N为PC中点，∴MN⊥PC，由（1）知MN⊥AB，即MN为异面直线PC和AB的公垂线，此时
，故能够确定满足条件的θ值，且θ值唯一.