高三数学第二次联合考试答案
一、1.B 2.C 3.C 4.A 5.C 6.C 7.C 8.D 9.B 10.A 11.B 12.B
二、13.-3
14. -1或6 15.(理)
(文)-2 16.①②④
三、17.解：由(
＜1得x2-x-6＞0，解得x＞3或x＜-2
A={xx＞3或x＜-2
4分
由log4(x+a)＜1得0＜x+a＜4
∴B={x-a＜x＜4-a 8分
∵A∩B=
,
∴
10分∴1≤a≤2
即a的取值范围是：{a1≤a≤2}12分
18.解：(Ⅰ)(z+1)(
+1)=z2,
∴
+1=z2
∵
=z2
∴z++1=0 3分
设z=x+ｙi(x,ｙk∈R),则=x-ｙi
∴x=-
,z=-+ｙi 5分
又∵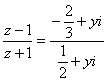
且是纯虚数
∴ｙ2-
=0且ｙ≠0 7分
∴ｙ=±
∴z=-±i 10分
(Ⅱ)当z=-+i时，argz=
11分
当z=--i时，argz=
12分
19.(Ⅰ)证明：∵ABCD是矩形∴CD⊥AD
又∵PA⊥平面ABCD，AD是PD在平面ABCD上的射影
由三垂线定理：CD⊥PD 3分
(Ⅱ)证明：取CD中点N，连结EN、FN
∵E、F分别是AB、PC的中点
∴FN∥PD,EN∥AD.
∵FN
平面PAD，EN平面PAD
∴FN∥平面PAD，EN∥平面PAD 5分
∵FN∩EN=N
∴平面EFN∥平面PAD
∵EF
平面EFN，
∴EF∥平面PAD 7分
(Ⅲ)解：当平面PCD与平面ABCD成45°角时，直线EF⊥平面PCD 8分
∵AB∥CD
∴CD⊥AD,PD⊥CD,即∠PDA就是侧面PCD与底面ABCD所成二面角的平面角.
连结PE，EC
又∠PDA=45°
∴PA=AD=BC,
又AE=EB
∴Rt△PAE≌Rt△CBE
∴PE=EC 10分
∵F为PC的中点
∴EF⊥PC，又FN∥PD,EN∥AD
∴CD⊥FN,∴CD⊥EN
∴CD⊥平面EFN
∴CD⊥EF
∵CD∩PC=C，
∴EF⊥平面PCD 12分
20.解：(Ⅰ)易知点P在抛物线C上，设PA的斜率为k
则直线PA的方程是ｙ-4=k(x-2) 1分
代入ｙ=-x2+6中，整理得：x2+2kx-4(k+1)=0
此时方程应有根xA及2，由韦达定理得：
2xA=-4(k+1)
∴xA=-2(k+1)
∴ｙA=k(xA-2)+4=-2k2-4k+4 4分
∴A(-2(k+1),-2k2-4k+4)
由于PA与PB的倾斜角互补，故PB方程的斜率为-k.
同理可得：B(-2(-k+1),-2k2+4k+4)
∴kAB=2 6分
(Ⅱ)由（Ⅰ）得∴直线AB的方程为：ｙ=2x+b,b＞0，
代入方程ｙ=-x2+6消去ｙ得：
x2+2x+b-6=0
AB=2
9分
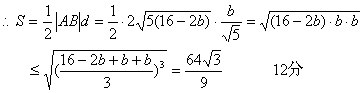
此时方程为：ｙ=2x+
13分
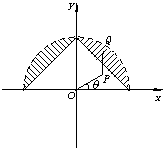21.(理)解：建立如图所示的直角坐标系，设机艇先沿OP方向前进m到P处，然后向北前进n到达Q，设∠XOP=θ，Q(x,ｙ)2分
可知
4分
∴AQ2=x2+ｙ2=m2+n2+2mnsinθ≤(m+n)2=400
∵机艇中途左拐
∴x2+ｙ2＜400 7分
又∵x+ｙ=m(sinθ+cosθ)+n=
·m+n≥m+n=20
即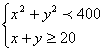
10分
根据题中的提示及对称性，结合上述不等式组，可得营救区域为上图所示阴影区域，但不包括圆周上的点. 12分
(文)解：设第n月月底所得现款an万元，
依题意an+1=an(1+20%)-an(1+20%)10%-0.3=1.08an-0.3 4分
化为an+1-
=1.08(an-)
则{an-}为等比数列，其中a1=1.08×10-0.3=(10-)×1.08+ 8分
∴an-=(10-)1.08n
即an=(10-)1.08n+ 10分
∴a12=(10-
)·1.0812+
代入1.0812≈2.5,得a12=19.375 12分
答：到这一年年底，个体户有现款193750元.
22.解：(Ⅰ)∵ak+1=ak+1+d,ak=ak+1-d
∴ak+2·ak=
又∵ak+1＞0,ak+2＞0,ak＞0
∴
4分
(Ⅱ)利用(Ⅰ)的结论可得
6分
令A=
，从而有
Ak＞
9分
又Ak=
从而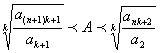
13分
(文)(Ⅰ)ｙn=2logaxn，
设{xn}的公比为q(q≠1)
∵ｙn+1-ｙn=2(logaxn+1-logaxn)=2loga
=2logaq
∴{ｙn}为等差数列，设公差为d 2分
∵ｙ3=18,ｙ6=12,
∴d=-2,
∴ｙn=ｙ3+(n-3)(-2)=24-2n
设前k项为最大，则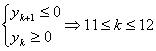
4分
∴前11项和前12项和为最大，其和为1325分
(Ⅱ)xn=a12-n,n∈N*
若xn＞1，则a12-n＞1
当a＞1时，n＜12，显然不成立 7分
当0＜a＜1时，n＞12，
∴存在M=12，13，14，…，
当n＞M时，xn＞1 9分
(Ⅲ)an=
10分
∵
12分
∴an+1＜an
∴n＞13时数列{an}为递减数列 13分