高三数学第二次月考
数 学 试 题
第Ⅰ卷（选择题 共60分）
一、选择题：本题共有12个小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一个是正确的.请将正确结论的代号填入答题卷选择题的答题卡表格中.
1．定义
,如果M＝{1，2，3，4，5},N＝{2，3，6}则M－N＝
(A) M (B) N (C) {1，4，5} (D){6}
2．已知命题p：若
则x、y全为0；命题q：若
给出下列四个复合命题：
①p且q，②p或q，③ ┓p，④ ┓q.其中真命题的个数为
(A) 1 (B) 2 (C) 3 (D) 4
3．已知函数
是奇函数，且在R上是增函数，则
(A) p>0，q=0 (B) p∈R，q=0 (C) p≤0，q＝0 (D) p≥0，q=0
4．函数
在区间（0，1）内有极小值，则实数a的取值范围是
(A)（0，3） (B)（－∞，3） (C)（0，＋∞） (D)（0，）
5．函数
的反函数是
(A) 
(B)
(C) 
(D)
6．已知某林区的森林积蓄量每年平均比上一年增长10.4％，经过x年可增长到原来的y倍，则函数y＝f（x）的图像大致是
|
| ||||
| ||||
7．若
成立，则正数a的取值范围是
(A)
(B)
(C)
(D)以上都不对
8．已知复数z满足z2 = i，i为虚数单位，则复数z等于
(A) 
(B) 
(C) 
(D) 
9．已知函数y = f (2x)的定义域为[－1，1]，则函数y = f (log2x)的定义域为
(A)[－1，1] (B)[，2] (C)[1，2] (D)[，4]
10．已知f (x+1)=－f (x)，且当x∈[0，1)时，f (x)=3x，则f (
)等于
(A) (B)－ (C) (D)－
11．将函数f (x)=2x的图象向左平移一个单位，得到图象C1，再将C1向上平移一个单位得到图象C2，作出C2关于直线y=x的对称图象C3，则C3的解析式为
(A) y=log2(x－1)－1 (B) y=log2(x+1)+1 (C) y=log2(x－1)＋1 (D) y=log2(x+1)－1
12．函数y = f (x)在区间（0，2）上是增函数，y = f (x+2)是偶函数，则下列结论正确的是
(A) f ( ) < f (1) < f ( ) (B) f ( )<f ( )< f (1)
(C) f (1)<f ( )<f ( ) (D) f ( )< f (1)<f ( )
第Ⅱ卷（非选择题 共90分）
二、填空题：本题共有4小题．只要求直接填写结果，每题填对得4分，否则一律是零分．本题满分16分.
13．已知
.
14．定义符号函数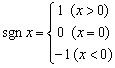
， 则不等式
的解集是 .
15．已知函数
在[1，＋∞）上是增函数，则实数a的取值范围是 .
16．给出下列四个命题：
①若
的极值；
②函数
在R上是奇函数；
③若点
的图象上，则函数
的定义域为
④ y＝f (x－2)与y＝f (2－x)的图象关于直线x＝2对称.
其中正确的命题序号是 .
三、解答题：本题共有6小题，要求写出解答过程和演算、证明步骤.本题满分74分.
17．（本题满分12分）
已知函数
的定义域为[1，4]，设函数
.
试求函数
的定义域和值域.
18．（本题满分12分）
已知函数f (x)＝loga（a>0，a≠1）
（1）求f (x)的定义域；
（2）判断f (x)的奇偶性；
（3）当0<a<1时，求使f (x)>0成立的x的取值范围.
19．（本题满分12分）
已知函数
为非零常数）
（1）解不等式
；
（2）设
时
的最小值为6，求
的值.
20．（本题满分12分）
设
分别是函数
的极小值点和极大值点，已知
.
求a的值及函数的极值.
21．（本题满分12分）
用水清洗一堆蔬菜上的残留农药，对用一定量的水清洗一次的效果作如下假定：用1个单位量的水可清洗掉蔬菜上的残留农药量的 ，用水越多，洗掉的农药量也多，但总是还有农药残留在蔬菜上.设用x单位量的水清洗一次后，蔬菜上的残留农药量与本次清洗前残留的农药量之比为函数f (x).
（1）试规定f (0)的值并解释其实际意义；
（2）试根据假定写出函数f (x)应满足的条件和具有的性质；
（3）设
，现有a(a>0)单位量的水可以清洗一次，也可以平均分成2份后清洗两次，试问用那种方案清洗后蔬菜上残留的农药量较小？
22．（本题满分14分）
已知二次函数
的图与x轴有两个不同的交点A、B且f (1)=0.
（Ⅰ）求
的范围；
（Ⅱ）证明
；
（Ⅲ）如果
是否均为正值？请说明理由.
参考答案与评分标准
一、第Ⅰ卷选择题答题处：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | D | C | A | D | B | C | D | B | A | A |
二、第Ⅱ卷填空题答题处：
13． -2；14. (－
，3) ； 15．（－1，1]
；16.
②、④
.
三、解答题：本题共有6小题，要求写出解答过程和演算、证明步骤.本题满分74分.
17．（本题满分12分）
解：由的定义域为[1，4]得
所以的定义域为[1，2].…………………………………6分
又＝
…………8分
∴当x＝1时，g(x)有最小值2；当x＝2时，g(x)有最大值7.∴2≤g(x)≤7…………10分
∴g(x)的值域为[2，7]……………………………………12分
18．（本题满分12分）
解：（1）由>0解得x>1或x<－1，
∴f (x)的定义域是（－∞，－1）∪（1，＋∞）………………………………4分
（2）f (－x)＝loga＝loga＝－ loga＝－ f (x)，
∴f (x)是奇函数.……………………………………………………………8分
（3）∵0<a<1，f (x)>0当且仅当0<<1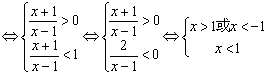
∴x<－1，即x的取值范围是（－∞，－1）………………………………12分
19．（本题满分12分）
解：（1）由
…………2分
①当a>0时，原不等式的解集为
………………………………4分
②当a<0时，原不等式的解集为
.…………………………6分
（2）
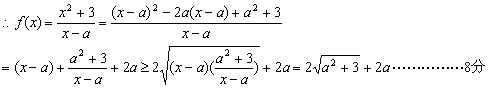
当且仅当
，……10分
由
20．（本题满分12分）
解：
，……………………………………2分
由已知得，是方程
的两个实根根，
即方程
的两个实根……………………………………4分
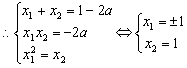………………………………………………6分
检验知：
………………………………………8分
当
时，
，当x<－1时，
，
在（－∞，－1）上是减函数；当－1<x<1时，
∴f (x)在（－1，1）上是增函数；当x>1时，，∴在（1，＋∞）上是减函数. ……………10分
∴极大值是f (1)＝3，极小值是f (－1)＝－5. …………………………12分
21．（本题满分12分）
解：（1）用0单位量的水清洗，蔬菜上的残留农药量与清洗前残留农药量相等，
∴f (0)=1.………………………………………………2分
（2）由题意f (x)应满足：f (0)＝1，f (1)＝，0<f (x)≤1，
f (x)在（0，＋∞）上递减.…………………………………………5分
（3）设用a(a>0)单位量的水清洗一次后，蔬菜上的残留农药量为P，清洗前残留农药量为S，则 ＝f (a)，∴P＝，………………………………6分
用 单位量的水清洗第一次后，蔬菜上的残留农药量为Q1，则 ＝f ( ),
∴Q1＝，………………………………7分
再用 单位量的水清洗第二次后，蔬菜上的残留农药量为Q2，则 ＝f ( )
∴Q2＝＝…………………………8分
∴
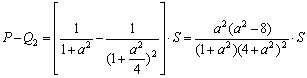.…………………………9分
当a>2时，P>Q2；
当a＝2时，P＝Q2；
当a<2时，P<Q2.………………………………………………11分
故当a超过2个单位水量时，分两次清洗好一些；当a不超过2个单位水量时，清洗一次效果好一些.…………………………………………12分
22．（本题满分14分）
解（Ⅰ）
若
.………………………………………………2分
矛盾.
又
得
……………………………………………………5分
（Ⅱ）
………………………………………………8分
由（Ⅰ）知
.…………………10分
（注也可用韦达定理求AB，酌情给分）
（Ⅲ）由题设条件得
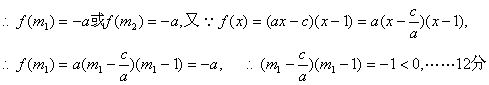
又当
上为增函数，
为正值.
同理可得
也是正值.……………………………………………………14分