高三第四次月考数学试题(文科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么它n次独立重复试验中恰好发生k次的概率
![]()
正棱锥、圆锥的侧面积公式S棱锥=![]() 其中c表示底面周长,
其中c表示底面周长,![]() 表示斜高或母线长。
表示斜高或母线长。
球的体积公式![]() 球=
球= ![]() 其中R表示球的半径
其中R表示球的半径
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设P={3,4,5},Q={4,5,6,7},定义P※Q=![]() ,则P※Q中元素的个数为 ( )
,则P※Q中元素的个数为 ( )
A.3 B.4 C.7 D.12
2.![]() 是直线
是直线![]() 垂直( )
垂直( )
A.充分而不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分又不必要的条件
3.某学生离家去学校,一开始跑步前进,跑累了再走余下的路程。下列图中纵轴表示离校
的距离,横轴表示出发后的时间,则较符合学生走法的是 ( )
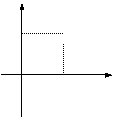 |  |  |  |
y y y y
o x o x o x o x
A B C D
4.准线方程为![]() 的抛物线的标准方程为 ( )
的抛物线的标准方程为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知直线a、b与平面α,给出下列四个命题
①若a∥b,b![]() α,则a∥α; ②若a∥α,b
α,则a∥α; ②若a∥α,b![]() α,则a∥b ;
α,则a∥b ;
③若a∥α,b∥α,则a∥b; ④a⊥α,b∥α,则a⊥b.
其中正确的命题是 ( )
A.1个 B.2个 C.3个 D.4个
![]() 6.如果命题“ (p或q)”为假命题,则
( )
6.如果命题“ (p或q)”为假命题,则
( )
A.p、q均为真命题 B.p、q均为假命题
C.p、q中至少有一个为真命题 D.p、q中至多有一个为真命题
7.若把一个函数的图象按![]() =(-
=(-![]() ,-2)平移后得到函数y=cosx的图象,则原图象的函数解析式为
( )
,-2)平移后得到函数y=cosx的图象,则原图象的函数解析式为
( )
A.y=cos(x+![]() )-2;
B.y=cos(x-
)-2;
B.y=cos(x-![]() )-2;
)-2;
C.y=cos(x+![]() )+2;
D.y=cos(x-
)+2;
D.y=cos(x-![]() )+2
)+2
8.已知一个简单多面体的各个顶点处都有三条棱,则顶点数V与面数F满足的关系式是( )
A.2F+V=4; B.2F-V=4;
C.2F+V=2; D.2F-V=2;
9.在正方体ABCD—A1B1C1D1中,B1C与对角面DD1B1B所成的角的大小是
A.15° B.30° C.45° D.60° ( )
10.点P是曲线![]() 上移动,设点P处切线倾斜角为
上移动,设点P处切线倾斜角为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.设F1,F2是双曲线![]() 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且![]() ,
,
则![]() 的值等于 ( )
的值等于 ( )
A.2 B.![]() C.4 D.8
C.4 D.8
12.在今年公务员录用中,某市农业局准备录用文秘人员二名,农业企业管理人员和农业法宣传人员各一名,报考农业公务员的考生有10人,则可能出现的录用情况种数是( )
A.5040 B.2520 C.1260 D.210
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分. 把答案填在题中横线上)
13.已知x、y满足约束条件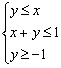 ,则z=2x+y的最大值是 。
,则z=2x+y的最大值是 。
14.某校有初中学生1200人,高中学生900人,老师120人,现用分层抽样方法从所有师生中抽取一个容量为N的样本进行调查,如果应从高中学生中抽取60人,那么N
.
15.已知![]() 分别为△ABC的三边,且
分别为△ABC的三边,且![]() .
.
16.已知下列四个函数:①![]() ②
②![]() ③
③![]() ④
④![]() .其中图象不经过第一象限的函数有 .(注:把你认为符合条件的函数的序号都填上)
.其中图象不经过第一象限的函数有 .(注:把你认为符合条件的函数的序号都填上)
三、解答题(本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
在某次考试中,甲、乙、丙三人合格(互不影响)的概率分别是![]() ,
,![]() ,
,![]() ,
,
考试结束后,最容易出现几人合格的情况?
18.(本题满分12分)
设![]()
![]() ,
,![]() 与
与![]() 的夹角
的夹角![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() 2,且
2,且![]() ,求
,求![]() 的值。
的值。
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分。
19.(本小题满分12分)
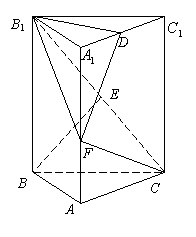
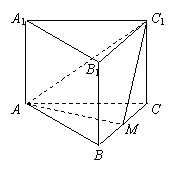 (甲)如图,正三棱柱
(甲)如图,正三棱柱![]() 的底面边长为
的底面边长为![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.
(Ⅰ) 求证点![]() 为边
为边![]() 的中点;
的中点;
(Ⅱ) 求点![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅲ) 求二面角![]() 的大小.
的大小.
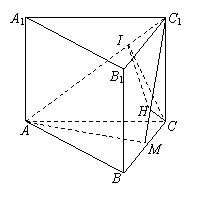
 (乙) 如图,直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=
(乙) 如图,直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=![]() ,BB1=
,BB1=![]() ,D为A1C1的中点,E为B1C的中点,
,D为A1C1的中点,E为B1C的中点,
(Ⅰ)求直线BE与A1C所成的角;
(Ⅱ)在线段AA1上是否存在点F,使CF⊥平面B1DF,若存在,求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
|
直线![]() 交于A、B
交于A、B
两点,以OA、OB为邻边作平行四边形OAPB(O为坐标原点).
(Ⅰ)若![]() ,且四边形OAPB为矩形,求a的值;
,且四边形OAPB为矩形,求a的值;
(Ⅱ)若![]() ,当k变化时(k∈R),求点P的轨迹方程.
,当k变化时(k∈R),求点P的轨迹方程.
21.(本小题满分12分)
把长240cm,宽90cm的矩形铁皮的四角切去相等的正方形,然后折成一个无盖的长方
体的盒子,角上切去的正方形的边长为多少时,盒子的容积最大. 最大容积是多少?
22.(本小题满分14分)
已知f(x)在(-1,1)上有定义,f(![]() )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(![]() )
)
(Ⅰ)证明:f(x)在(-1,1)上为奇函数;
(Ⅱ)对数列x1=![]() ,xn+1=
,xn+1=![]() ,求f(xn);
,求f(xn);
(Ⅲ)求证![]()
第四次月考
数学试题(文科)
参考答案
一、选择题:5×12=60
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | D | B | A | C | D | B | B | B | A | B |
二、4×4=16分 13、3 14、148 15、 ![]() 16、①,④
16、①,④
三解答题:共74分
17. 按以下四种情况计算概率,概率最大的就是最容易出现的情况.
⑴三人都合格的概率![]() ……………………………………………2分
……………………………………………2分
⑵三人都不合格的概率为![]() …………………… 4分
…………………… 4分
⑶恰有两人合格的概率
![]() ………………………7分
………………………7分
⑷恰有一人合格的概率![]() ……………………………… 10分
……………………………… 10分
由此可知,最容易出现恰有1人合格的情况…………………………………………12分
18:![]() =
=![]()
![]()
∵![]() (0,
(0,![]() ),
),![]() ,∴
,∴![]() …………………………….4
…………………………….4
∴![]() ∴
∴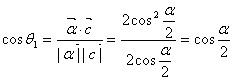 ………………8
………………8
∴![]()
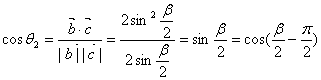 ……………………10
……………………10
∴![]() 由
由![]() =
=![]() ∴
∴![]() ∴
∴![]() =(
=(![]() )=
)=![]() 。……….12
。……….12
19、(甲)解: (Ⅰ) ![]()
![]() 为以点M为直角顶点的等腰直角三角形,
为以点M为直角顶点的等腰直角三角形,
![]()
![]() .
.
![]() 正三棱柱
正三棱柱![]() ,
,
![]()
![]() 且
且![]() . …………………………2分
. …………………………2分
![]()
![]() 在底面内的射影为
在底面内的射影为![]() ,
,![]() .
.
![]()
![]() ,
,
![]() 点
点![]() 为
为![]() 边的中点.
……………………………………………4分
边的中点.
……………………………………………4分
 (Ⅱ) 过点
(Ⅱ) 过点![]() 作
作![]() ,
,
由(Ⅰ)知![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() , ……………………………………………6分
, ……………………………………………6分
由(Ⅰ)知,![]() ,
,![]() 且
且![]() .
.
![]()
![]() .
.
![]()
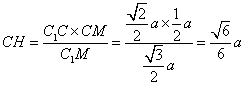 .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为底面边长为
的距离为底面边长为![]() . ………………………8分
. ………………………8分
(Ⅲ) 过点![]() 作
作![]() ,
,
![]()
![]() ,
,
![]()
![]() 为
为![]() 在平面
在平面![]() 内的射影,
内的射影,
![]()
![]() ,
,![]() 是二面角
是二面角![]() 的平面角.……………10分
的平面角.……………10分
在直角三角形![]() 中,
中,
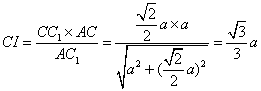 ,
,
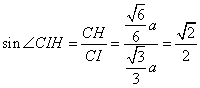 ,
,
![]()
![]() ,
,
![]() 二面角
二面角![]() 的大小为45O.
…………………………………12分
的大小为45O.
…………………………………12分
(乙) 解: (Ⅰ)以![]() 为原点,建立如图所示的空间直角坐标系.……1分
为原点,建立如图所示的空间直角坐标系.……1分
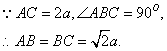
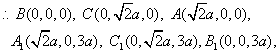
![]() ,
……………………………3分
,
……………………………3分
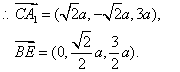 ,
,
![]() ,
,
![]() ,
,
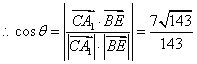 .
…………………5分
.
…………………5分
故![]() 与
与![]() 所成的角为
所成的角为![]() . …………………………………6分
. …………………………………6分
(Ⅱ)假设存在点![]() ,使
,使![]() ,不妨设
,不妨设![]() ,
,
![]() ,
,
![]() , ……………………8分
, ……………………8分
![]() ……………………9分
……………………9分
由![]() , …………………11分
, …………………11分
故当![]() .………………………………12分
.………………………………12分
20.解(Ⅰ)设![]() …………2分
…………2分

![]() ,………………………………4分
,………………………………4分
![]() ……………………………………6分
……………………………………6分
(Ⅱ)设![]()
因为A、B在椭圆![]()
相减得![]() ……………………………………9分
……………………………………9分
所以 …………………………………………11分
…………………………………………11分
![]() ……………12分
……………12分
21:设切去的正方形的边长为![]() cm,则折成的无盖的长方体 底面边长为
cm,则折成的无盖的长方体 底面边长为![]() cm和
cm和![]() cm(2分),高为
cm(2分),高为![]() cm,于是盒子的容积(单位:
cm,于是盒子的容积(单位:![]() )
)
![]() ………………………………….4分
………………………………….4分
又由![]() ,得
,得![]() .
. ![]() .(6 分)
.(6 分)
令![]() ,得
,得![]() ,由
,由![]() ,解得
,解得![]() ….8分
….8分![]() 当
当![]() 时,
时,![]() 时,
时,![]() ,因此当
,因此当![]() 时,V有最大值…….10分
时,V有最大值…….10分
最大容积![]() ………………………12分
………………………12分
22.(Ⅰ)证明:令x=y=0,∴2f(0)=f(0),∴f(0)=0
令y=-x,则f(x)+f(-x)=f(0)=0
∴f(x)+f(-x)=0 ∴f(-x)=-f(x)
∴f(x)为奇函数 ……………………………………………………..4分
(Ⅱ)解:f(x1)=f(![]() )=-1,f(xn+1)=f(
)=-1,f(xn+1)=f(![]() )=f(
)=f(![]() )=f(xn)+f(xn)=2f(xn)
)=f(xn)+f(xn)=2f(xn)
∴![]() =2即{f(xn)}是以-1为首项,2为公比的等比数列
=2即{f(xn)}是以-1为首项,2为公比的等比数列
∴f(xn)=-2n-1……………………………………………………………………..8分
(Ⅲ)解:![]()
![]()
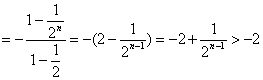 ………………………………………10分
………………………………………10分
而![]()
∴![]() ……………………………………….14分
……………………………………….14分![]()