高三第一次模拟数学试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。第I卷1至2页,第II卷3至8页,共150分钟,考试时间120分钟。
第I卷(选择题 共60分)
一. 选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将你认为正确的选项填在题后括号内)
1. 已知映射:![]() ,其中集合A={
,其中集合A={![]() },集合B中的元素都是A中元素在映射f下的象,且对任意的
},集合B中的元素都是A中元素在映射f下的象,且对任意的![]() 在B中和它对应的元素是 a ,则集合B中元素的个数是( )
在B中和它对应的元素是 a ,则集合B中元素的个数是( )
A. 4 B. 5 C. 6 D. 7
2. 已知复数Z,若![]() ,则M是( )
,则M是( )
A. M={虚数} B. M={实数}
C. {实数}![]() M
M ![]() {复数} D.
M={复数}
{复数} D.
M={复数}
3. 已知等差数列![]() 满足
满足![]() ,则有( )
,则有( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
4. 如图是正方体的平面展开图,在这个正方体中
(1)BM与ED平行 (2)CN与BE是异面直线
(3)CN与BM成![]() (4)DN与BN垂直
(4)DN与BN垂直
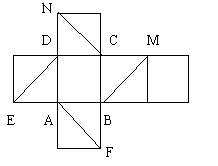
以上四个命题中,正确命题的序号是( )
A. (1)(2)(3) B. (2)(4)
C. (3)(4) D. (2)(3)(4)
5. 设![]() ,
,![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
6. 已知![]() ,函数
,函数![]() 在
在![]() 上是单调增函数,则a的最大值是( )
上是单调增函数,则a的最大值是( )
A. 3 B. 2 C. 1 D. 0
7. 锐角三角形中,![]() 分别是内角A,B,C的对边,设B=2A,则
分别是内角A,B,C的对边,设B=2A,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
(0,2)
D.
(0,2)
8. 路灯距地平面为8m,1个身高为1.6m的人以84米/分的速率在地平面上,从路灯在地平面上的射影C,沿某直线CD离开路灯(如图)
那么人影长度的变化速率![]() 为( )米/秒
为( )米/秒
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()

9. 如果![]() 是两个不相等的正整数,则
是两个不相等的正整数,则![]() 等于( )
等于( )
A. ![]() B.
B.
![]() C.
0 D.
1
C.
0 D.
1
10. 双曲线![]() 的离心率
的离心率![]() ,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则
,点A与F分别是双曲线的左顶点和右焦点,B(0,b),则![]() 等于( )
等于( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11. 一天内的不同时刻,经理把文件交给秘书打字,每次都将文件放在秘书文件垛的最上面,秘书有时间就将文件垛最上面的文件取来打,若经理将5份文件在不同时刻按(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)的顺序交来,则秘书的打字顺序不可能是( )
(5)的顺序交来,则秘书的打字顺序不可能是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
12. 已知![]() 且
且![]() ,
,![]() ,当
,当![]() 时均有
时均有![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
第II卷(非选择题 共90分)
二. 填空题:本大题共4个小题,每小题4分,共16分,把答案填在题中横线上。
13. 圆![]() 在不等式组
在不等式组![]() 所表示的平面区域中所占的面积为________。
所表示的平面区域中所占的面积为________。
14. 从6台原装计算机和5台组装计算机中任选5台,其中至少有原装和组装计算机各两台的概率是________。
15. 有三个球和一个正方体,第一个球与正方体各个面相内切,第二球与正方体各条棱相切,第三个球过正方体各顶点,则这三个球的面积之比为________。
16. 设函数![]() ,给出以下四个结论:
,给出以下四个结论:
(1)它的周期为![]() :(2)它的图象关于直线
:(2)它的图象关于直线![]() 对称;(3)它的图象关于点
对称;(3)它的图象关于点![]() 对称;(4)在区间(
对称;(4)在区间(![]() ,0)上是增函数。
,0)上是增函数。
以其中两个论断作为条件,另两个论断作结论写出你认为正确的一个命题_________
三. 解答题:本大题共6个小题,满分74分,解答应写出文字说明演算步骤。
17. (本小题满分10分)
一名学生骑自行车上学,从他的家到学校的途中有6个交通岗,假设他在各个交通岗遇到红灯的事件是独立的,并且概率都是![]()
(1)求这名学生首次遇到红灯前,已经过了两个交通岗的概率:
(2)求这名学生在途中遇到红灯数§的期望和方差。
18. (本小题满分12分)
设![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,且
,且![]()
![]() ,求
,求![]() 的值。
的值。
19. (本小题满分12分)
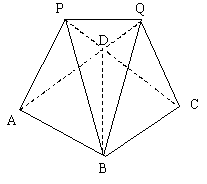
如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面![]() 内作菱形ABCD,其边长为1,
内作菱形ABCD,其边长为1,![]() ,再在平面
,再在平面![]() 的上侧,分别以
的上侧,分别以![]() 与
与![]() 为底面安装上相同的正三棱锥
为底面安装上相同的正三棱锥![]() 与
与![]() 。
。
(1)求证:![]()
(2)求二面角![]() 的大小;
的大小;
(3)求点P到平面![]() 的距离
的距离
20. (本小题满分12分)
已知等比数列![]() ,求证:对任意
,求证:对任意![]() ,方程
,方程![]() 都有一个相同的根,且另一个根
都有一个相同的根,且另一个根![]() 仍组成一个等比数列
仍组成一个等比数列![]() 。
。
21. (本小题满分14分)
已知A(![]() ,0),B(2,0),动点P与A、B两点连线的斜率乘积为
,0),B(2,0),动点P与A、B两点连线的斜率乘积为![]()
(1)根据k的取值情况,讨论点P的轨迹类型。
(2)若点P的轨迹为焦点在y轴上的椭圆,且下顶点到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的值。
的值。
22. (理科 本小题满分14分)
已知函数![]() 的定义域为R,对任意
的定义域为R,对任意![]() 都有
都有![]() 且
且![]() 时,
时,![]()
(1)试判断函数![]() 的奇偶性;
的奇偶性;
(2)试判断在区间![]() 上,
上,![]() 是否有最大值或最小值?如果有,求出其最大值或最小值;如果没有,说明理由;
是否有最大值或最小值?如果有,求出其最大值或最小值;如果没有,说明理由;
(3)解关于![]() 的不等式
的不等式![]()
22. (文科 本小题满分14分)
已知函数![]() ,若函数
,若函数![]() 图象上任意一点P关于原点对称Q的轨迹恰好是函数
图象上任意一点P关于原点对称Q的轨迹恰好是函数![]() 的图象
的图象
(1)写出函数![]() 的解析式;
的解析式;
(2)求不等式![]()
![]() 的解集。
的解集。
【试题答案】
一. 选择题
1. A 2. B 3. C 4. C 5. D 6. A 7. B 8. A 9. B
10. C 11. D 12. C
二. 填空题
13. ![]() 14.
(理)
14.
(理)![]() (文)
(文)![]() 15.
1:2:3
15.
1:2:3
16. ![]()
三. 解答题:
17. (理)
解:(1)![]() 这名学生第一、第二交通岗未遇到红灯,第三个交通岗遇到红灯 2分
这名学生第一、第二交通岗未遇到红灯,第三个交通岗遇到红灯 2分
![]() 5分
5分
(2)![]() 6分
6分
![]() 8分
8分
![]() 10分
10分
(文)解:(1)从中买1张彩票获得二等奖的概率为![]() 2分
2分
从中买1张彩票获得三等奖的概率为![]() 4分
4分
![]() 从中买1张彩票获得二等奖或三等奖的概率为:
从中买1张彩票获得二等奖或三等奖的概率为:
![]() 6分
6分
(2)![]() 从中买1张彩票中奖的概率为
从中买1张彩票中奖的概率为![]() 8分
8分
![]() 从中买1张彩票不中奖的概率为
从中买1张彩票不中奖的概率为![]() 10分
10分
18. (理)
解:![]() 2分
2分
![]() 4分
4分
又![]()
![]()
故![]() 6分
6分
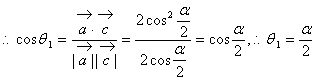 8分
8分
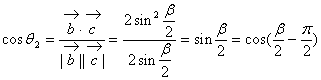
![]() ,
,![]() 10分
10分
又![]()
![]() ,即
,即![]() 11分
11分
![]() 12分
12分
文(解):
![]() 2分
2分
![]() 3分
3分
又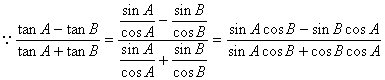
![]() 7分
7分
![]()
即![]() 10分
10分
![]() 11分
11分
![]()
![]() 为等边三角形 12分
为等边三角形 12分
19. (1)证明
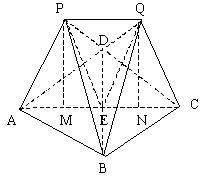
![]() 是相同的正三棱锥
是相同的正三棱锥
![]() 是全等的等腰三角形 1分
是全等的等腰三角形 1分
取BD中点E,连结PE,QE
则![]()
![]() 平面PQE 3分
平面PQE 3分
从而![]() 4分
4分
(2)证明:由(1)知![]() 是二面角
是二面角![]() 的平面角 5分
的平面角 5分
作![]() ,垂足为M,作
,垂足为M,作![]() ,垂足为N,则PM//QN,M,N分别为正
,垂足为N,则PM//QN,M,N分别为正![]() 与正
与正![]() 的中心,从而A,M,E,N,C在一条直线上。 6分
的中心,从而A,M,E,N,C在一条直线上。 6分
PM与QN确定平面PACD且PMNQ为矩形
经计算![]() ,
,![]() 8分
8分
![]()
![]() 二面角
二面角![]() 为
为![]() 9分
9分
(3)解:由(1)知![]() 平面PEQ,设点P到平面QBD的距离为h
平面PEQ,设点P到平面QBD的距离为h
则![]() 10分
10分
又![]() 11分
11分
![]()
即点P到平面QBD的距离为![]() 12分
12分
20. (理)
证明:(1)![]() 数列
数列![]() 为等比数列
为等比数列
![]() 2分
2分
故![]() 总满足方程
总满足方程![]()
因此方程有一个公共根![]() 5分
5分
(2)当n依次取正整数时,设方程另一个根为![]() 数列
数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,根据韦达定理有
,根据韦达定理有
![]() 7分
7分
即![]() 9分
9分
而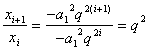 11分
11分
因此数列![]() 是以
是以![]() 为公比的等比数列 12分
为公比的等比数列 12分
(文)
解:(1)设等比数列![]() 公比为
公比为![]()
![]() 2分
2分
![]() 数列
数列![]() 是以
是以![]() 为公差的等差数列 3分
为公差的等差数列 3分
(2)由:![]() ,即
,即![]()
![]() 即
即![]() 5分
5分
由已知得![]() 解得
解得![]() 或
或![]() 6分
6分
由![]() 求得
求得![]() 7分
7分
此时![]()
![]() 9分
9分
由![]() 求得
求得![]() 10分
10分
此时![]() 12分
12分
21. 解:
(1)设点P的坐标为(![]() ),则
),则
![]() ,即
,即![]() 2分
2分
![]() ,
,![]() 动点P的轨迹方程为
动点P的轨迹方程为![]() 4分
4分
当![]() 时,点P的轨迹为双曲线(除去两顶点(
时,点P的轨迹为双曲线(除去两顶点(![]() ,0)) 5分
,0)) 5分
当![]() 时,且
时,且![]() 时,点P的轨迹为椭圆(除去两顶点(
时,点P的轨迹为椭圆(除去两顶点(![]() ,0)) 6分
,0)) 6分
当![]() 时,点P的轨迹为圆(除去两点(
时,点P的轨迹为圆(除去两点(![]() ,0)) 7分
,0)) 7分
(2)![]() 点P的轨迹为焦点在
点P的轨迹为焦点在![]() 轴上的椭圆
轴上的椭圆![]()
![]() 9分
9分
下顶点坐标为![]() 11分
11分
![]() 点到直线
点到直线![]() 的距离为
的距离为![]()
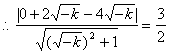 ,解得
,解得![]() (满足
(满足![]() ) 14分
) 14分
22. (理)
解:(1)由![]() ,令
,令![]() 得
得![]()
而![]() ,即
,即![]()
![]() 为奇函数 2分
为奇函数 2分
(2)当![]() 时,由
时,由![]() 时
时![]() 有
有
![]()
![]() 是减函数 4分
是减函数 4分
从而![]() 在
在![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]()
最小值![]() 6分
6分
最大值![]()
(3)![]()
![]() 7分
7分
![]()
![]() 即
即![]()
![]() 9分
9分
![]() 当
当![]() 时
时![]() 10分
10分
![]() 当
当![]() 0时
0时![]() 11分
11分
![]() 当
当![]() 时
时![]() 12分
12分
![]() 当
当![]() 时
时![]() 13分
13分
![]() 当
当![]() 时
时![]() 14分
14分
(文)解:
(1)设![]() 图象上任意一点P(
图象上任意一点P(![]() )则
)则![]() ,P点关于原点的对称点
,P点关于原点的对称点
Q(![]() )在
)在![]() 的图象上 2分
的图象上 2分
![]() ,
,![]() 4分
4分
![]() 5分
5分
(2)![]()
![]() 在
在![]() 即
即![]() 前提下 7分
前提下 7分
![]() 8分
8分
(1)当![]() 时
时![]() ,即
,即![]()
又![]() 10分
10分
(2)当![]() 时
时![]() ,
,![]() 或
或![]()
又![]() 12分
12分
总之,当![]() 时
时![]() ,当
,当![]() 时
时![]() 14分
14分