高三年级模拟考试题(二)
数 学
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项符合题目要求.)
1.已知x1是方程x+lgx=3的根,x2是方程x+10x=3的根,则x1+ x2等于 ( )
A.6 B.3 C.2 D.1
2.使集合M={xax2+2x+a=0,a∈R}中有且只有一个元素的所有a的值组成的集合N的子集个
数为 ( )
A.2 B.4 C.7 D.8
|
A.b∈(-∞,0)
B.b∈(0,1)
C.b∈(1,2)
D.b∈(2,+∞)
4.设有n个样本x1,x2,……,xn,其标准差为Sx,另有n 个样本y1,y2,……yn,且yk=3xk+5
(k=1,2,…,n),其标准差为Sy,则下列关系正确的是 ( )
A.Sy=![]() Sx+5 B.Sy=3 Sx+5
Sx+5 B.Sy=3 Sx+5
C.Sy=3 Sx D.Sy=![]() Sx
Sx
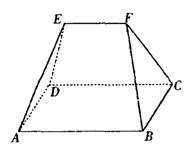
5.如图,在多面体ABCDEF中,已知ABCD是面积为2S的正方形,EF∥AB,2EF=AB.EF
|
A.![]()
B.![]()
C.![]()
D.![]()
6.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06(0.50[m]+1)元给出,其中[m]表示大
于或等于m的最小整数,如[3]=3,[3.1]=4,[3.7]=4,若从甲地到乙地的通话费为4.24元,
则m的取值范围是 ( )
A.[4,6] B.(5,6![]() C.(5,6) D.[5,6
C.(5,6) D.[5,6![]()
7.设P为椭圆上一点,且∠PF1F2=30°,∠PF2F1=45°,其中F1、F2为椭圆的两个焦点,
则椭圆的离心率e的值等于
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.点P在曲线y=x3-x+7上移动,过P点的切线的倾斜角取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.函数![]() 的最小正周期是 ( )
的最小正周期是 ( )
A.![]() B.π C.2π D.4π
B.π C.2π D.4π
10.长为2的线段PO⊥平面α,O为垂足,A、B是平面α内两动点,若tan∠PAO= ![]() ,
,
tan∠PBO=2,则P点到直线AB的距离的最大值是 ( )
A.2![]() cm B.
cm B.![]() cm C.
cm C.![]() cm D.
cm D.![]() cm
cm
11.已知![]() 成等比数列,则xy的 ( )
成等比数列,则xy的 ( )
A.最大值是![]() B.最大值是
B.最大值是![]()
C.最小值是![]() D.最小值是
D.最小值是![]()
12.已知点M(-3,0),N(3,0),B(1,0),⊙C与直线MN切于点B,过M、N与⊙
C相切的两直线相交于点P,则P点的轨迹方程为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(本大题共4小题,每空4分,共16分,把答案填在题中横线上.)
13.![]() 的展开式中,奇次项系数和为
.
的展开式中,奇次项系数和为
.
14.已知![]() 上投影是
.
上投影是
.
15.将自然数1,2,3,…,n,按第K组含K个数的规则依次分组:(1),(2,3),(4,5,
6),…,那么2003所在组的序号为 .
16.某邮局只有0.60元,0.80元,1.10元三种邮票,现有邮资7.50元的邮件一件,为使粘
贴邮票的张数最少,且邮资恰好为7.50元,则最少要购买邮票 张.
三、解答题(本大题共6小题,共74分.解答应有证明过程或演算步骤)
17.(本题满分12分)
已知函数![]() 的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(x0,2) 和(x0+3π,-2).
的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(x0,2) 和(x0+3π,-2).
(1)求![]() 的解析式;
的解析式;
(2)将y=![]() 图象上所有点的横坐标缩短到原来的
图象上所有点的横坐标缩短到原来的![]() (纵坐标不变),然后再将所得图象向x轴正方向平移
(纵坐标不变),然后再将所得图象向x轴正方向平移![]() 个单位,得到函数y=g(x)的图象,写出函数y=g(x)的解析式.
个单位,得到函数y=g(x)的图象,写出函数y=g(x)的解析式.
18.(本题满分12分)
长方体ABCD—A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
(1)求二面角E—AD1—A1大小的正切值;
(2)求A1点到平面AED1的距离.
19.(本题满分12分)袋中有4个红球,3个黑球,今从袋中随机取出4个球,设取到一个
红球得2分,取到一个黑球得1分.
(1)(文)求可能得分ξ的取值及相应的概率;
(2)(理)求得分ξ的概率分布和数学期望.
20.(本题满分12分)
已知![]() 是定义在[-1,1]的奇函数,且f(1)=1,若a、b∈[-1,1],a+b≠0时,有
是定义在[-1,1]的奇函数,且f(1)=1,若a、b∈[-1,1],a+b≠0时,有
![]()
(1)判断函数![]() 在[-1,1]上是增函数还减函数,并证明你的结论;
在[-1,1]上是增函数还减函数,并证明你的结论;
(2)解不等式![]()
(3)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范
的取值范
围.
21.(本题满分12分)
已知双曲线![]() 的左右两焦点为F1、F2,又点P在双曲线上,使PF1、F1F2、PF2成等比数列,且PF2<4,求该双曲线方程.
的左右两焦点为F1、F2,又点P在双曲线上,使PF1、F1F2、PF2成等比数列,且PF2<4,求该双曲线方程.
22.(本题满分14分)
某下岗人员为再就业,一月初向银行贷款10万元作为开店资金,每月底获得的利润是该月初投放资金的20%,每月底需交房租和所得税为该月所得金额(含利润)的10%,每月生活费和其它开支3000元,余款作为资金全部投入再营业.如此继续,那么到这一年底,这个人有现款多少元(假设没有赊销)?若银行贷款的年利率为25%,则这个人还清银行贷款后,纯收入还有多少元?
高三年级模拟考试题(二)
数学参考答案
一、选择题(12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | A | C | A | B | B | D | B | C | D | B |
二、填空题(每题4分,共16分)
13. 4; 14.![]() 15.63; 16.8;
15.63; 16.8;
三、解答题(共6个题,共74分)
17.(满分12分)
(1)![]() ……6分 (2)
……6分 (2)![]() …………12分
…………12分
18.(满分12分)
(1)推导得二面角E—AD1—A1大小正切为![]() .………6分
.………6分
(2)求得距离为![]() …………6分
…………6分
19.(满分12分)
(1)(文)ξ=5,6,7,8……6分 相应概率为![]() ,……12分
,……12分
|
(2)(理)ξ的分布列 ……6分
Eξ=![]() ………………12分
………………12分
20.(满分12分)
(1)增函数…………4分
(2)![]() R}…………8分
R}…………8分
(3)m≤-2或m=0或m≥2…………12分
21.(满分12分)
解:![]() 点在右支上.……2分
点在右支上.……2分
设![]()
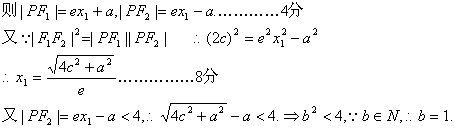
∴所求方程为:![]() …………12分
…………12分
22.(满分14分)
略解:(1+20%)×105-(1+20%)×105×10%-3×103=1.05×105…………2分
an+1= an(1+20%)-an(1+20%)×10%-3×103=1.08 an-3×103(n≥1)…………4分
于是an+1-3.75×104=1.08(an-3.75×104)………………6分
∴an+1-3.75×104=1.08(a1-3.75×104)×1.08n-1
∴an=6.75×104×1.08n-1+3.75×104…………………………8分
∴a12=6.75×104×1.0811+3.75×104…………………………10分
即这个人在该年底有现款1.94886×105元………………12分
还贷后纯收入为a12-(1+25%)×105=69886元……………………14分