全 国 统 一 大 联 考
高三年级数学检测卷
内容：高中数学第三册（试验·修订本）
考生注意：
1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。
2、答题前，考生务必将密封线内项目填写清楚。
3、请将第Ⅰ卷各题答案填在第Ⅱ卷前答题卡上。
4、第Ⅱ卷用蓝黑钢笔或圆珠笔答题。
第Ⅰ卷（选择题，共60分）
一、选择题（本大题共12小题，每小题5分，共60分，每小题只有一个选项符合题意。）
1、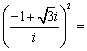
（ B ）
A．
B．
C．
D．
2、
且满足
，则
的值为（ B ）
A．
； B．
； C．
； D．
3、设
，若
，则
的取值范围是（ D ）
A．
； B．
； C．
； D．
4、若
是方程
的一个根，则使
的实数的取值范围为（ D ）
A．
； B．
； C．
； D．
5、已知向量
，则
为（ D ）
A．
；
B．
；
C．
；
D．1
6、地球仪上北纬
圈的周长为
，则该地球仪的体积为（ B ）
A．
； B．
； C．
； D．
７、已知双曲线的中心在原点，两个焦点
坐标分别为
和
，P在双曲线上，满足
且
的面积为1，则此双曲线的方程是（C ）
A．
； B．
； C．
； D．
8、已知
为原点，
其中为常数且
，则
的最小值是（ D ）
A．
；
B．
； C．
；
D．
9、要排一张有5个独唱节目和3个合唱节目的演出节目表，如果合唱节目不排在节目表的第一个位置上，并且任何两个合唱节目不能相邻，则不同的排法种数是（ B ）
A．14400； B．7200； C．3600； D．1800
10、设
展开式中
的系数为
（其中
），则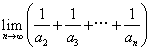
为（ B ）
A．2；
B．1；
C．；
D．
11、若直线
始终平分圆
的周长，则
的取值范围是（ A ）
A．
； B．； C．
； D．
12、甲烷分子由一个碳原子和四个氢原子组成，其空间构型为一个正四面体，碳原子位于正四面体的中心，四个氢原子分别位于该四面体的四个顶点上。若将碳原子和氢原子均视为一个点（体积忽略不计），且已知氢原子间的距离为，则碳原子和氢原子间的距离为（ D ）
A．
；
B．
； C．
；
D．
第Ⅱ卷（非选择题）
二、填空题（每小题4分，共16分）
13、设数列
满足
，且
，则
11 .
14、已知
是定义在
上的奇函数，它的最小正周期是3，则
0.
15、已知
，则
与
的大小关系是f(1/3)>f(1/2).
16、设函数
和下面的7个论断：
①在
上是增函数； ②有最大值1；
③有最小值0；
④的图象过
点；
⑤的图象过
点； ⑥在
上为增函数；
⑦
。
写出一个函数
的解析式，使它满足上面的7个论断中的4个论断即可，
1-x-1.
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。）
17、（本小题满分12分）
已知：
,且
的最小正周期
。若
对于正的常数
和任意实数
都成立，判断是否是周期函数？如果是，猜测是多少，并加以证明。
解：f(x)是周期函数，其周期是4m，下面给出具体的证明。
18、（本小题满分12分）
一名学生骑自行车上学，从他的家到学校的途中有6个交通岗，假设他在各交通岗遇到红灯的事件是独立的，并且概率都是
（1）求这名学生首次遇到红灯前，已经过了两个交通岗的概率；
（2）求这名学生在途中遇到红灯数
的期望与方差。
解：（1）当这名学生首次遇到红灯前，已经过了两个交通岗的，则必须是这个学生通过第一个交通岗和第二个交通岗都遇到绿灯，且通过第三次交通岗时是红灯，遇到绿灯的概率是1-1/3=2/3，且它们彼此之间互相独立，
所以所求的概率是P=
答………
(2)途中遇到红灯数满足~B(6,1/3)期望E=6*1/3=2
方差D=6*1/3*2/3=4/3
答…
19、（本小题满分12分）
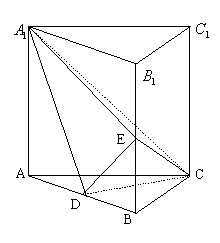如图，直三棱柱
中，
为
中点，
（1）求证：
（2）求二面角
的大小；
（3）求三棱锥
的体积。
20、（本小题满分12分）
已知函数
，数列是公差为
的等差数列，
是公比为
的等比数列，若
。
（1）求数列和的通项公式；
（2）设数列
的前
项和
为，且对一切自然数均有：
成立，求
。
21、（本小题满分12分）
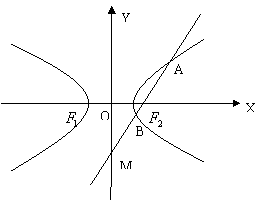
如图：双曲线
的两个焦点分别为，斜率为
的直线
过焦点
与双曲线交于
两点，与
轴交于点
，若
。
（1）求双曲线离心率
的值；
（2）若弦
的中点到右准线的距离为
时，求双曲线的方程。
22、（本小题满分14分）
已知两个函数
，其中
为实数。
（1）对任意的
，都有
成立，求的取值范围。
（2）对任意的
，
，都有
，求的取值范围。