高三年级数学月考

高三年级数学月考

数　　学

　　本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页。第Ⅱ卷3至10页。考试结束后，只收答题卡。

第Ⅰ卷（选择题 共60分）

注意事项：

1．答第Ⅰ卷前，考生务必将自己的班别、学号、姓名用钢笔或圆珠笔写在答题卡上。

2．每小题选出答案后，用钢笔或圆珠笔在答题卡上对应题目的位置填上你的答案，如需改动，用橡皮擦干净后，再填上其它答案，不能答在试题卷上。

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有

一项是符合题目要求的。

1．（2003年春季高考北京卷－理1）若集合　　　（　　）

　　　A．　　　　　 B．　　　　　 C．　　　　　D．

2．（2003年高考上海卷－理15）a₁、b₁、c₁、a₂、b₂、c₂均为非零实数，不等式a₁x²+b₁x+c₁>0和a₂x²+b₂x+c₂>0的解集分别为集合M和N，那么“”是“M=N”的　　　　　 （　　）

　　　　　　　　　　　　　　　　　　　 A．充分非必要条件.　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．必要非充分条件.

　　　　　　　　　　　　　　　　　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既非充分又非必要条件.

3．（2003年高考广东卷5）设函数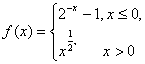若，则x₀的取值范围是（　　）

　　　A．（－1，1）　　　　　　　　　　　　　　　　　　　　　B．（－1，+∞）

　　　C．（－∞，－2）∪（0，+∞）　　　　　　　 D．（－∞，－1）∪（1，+∞）

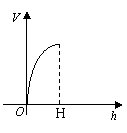4．向高为H的水瓶中注水，如果注水量V与水深h的函数关系如右图所示，那么水瓶的形状是（　　）

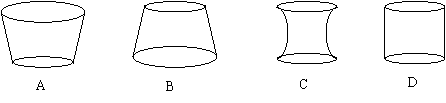5．（2003年高考江苏卷6）函数的反函数为（　　）

　　　 A．　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　 D．

6．（2003年高考全国卷－文7）已知　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　 C．　　　　　　　　 D．

7．（2003年高考上海卷－文15）在P（1，1）、Q（1，2）、M（2，3）和N四点中，函数的图象与其反函数的图象的公共点只可能是点　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　　　　　　　　　　　　　　　　　 A．P．　　　　　　　　　 B．Q.　　　　　　　　　　　　C．M.　　　　　　　D．N.

8．（2003年高考北京卷－理2）设，则（　　）

　　　 A．y₃>y₁>y₂　　　　　　 B．y₂>y₁>y₃　　　　　　 C．y₁>y₂>y₃　　　　　　 D．y₁>y₃>y₂

9．（2003年高考江苏卷9）已知方程的四个根组成一个首项为的等差数列，则m－n=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．1　　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　　D．

10．（2003年高考北京卷－理9）若数列的通项公式是，则　 等于　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　　　D．

11．（2003年高考天津卷－理1）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）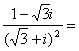

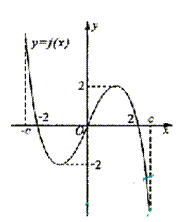　　　A．　　　　　　 B．　　　 C．　　　　　　 D．

12．（2003年高考上海卷－理16）f()是定义在区间[－c,c]上的奇函数，其图象如图所示：令g（）=af（）+b，则下列关于函数g（）的叙述正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　　　　　　　　　　　　　　　　　 A．若a<0,则函数g（）的图象关于原点对称.

　　　　　　　　　　　　　　　　　　　 B．若a=－1，－2<b<0,则方程g（）=0有大于2的实根.

　　　　　　　　　　　　　　　　　　　 C．若a≠0,b=2,则方程g（）=0有两个实根.

　　　　　　　　　　　　　　　　　　　 D．若a≥1,b<2,则方程g（）=0有三个实根.

13．（2003年高考上海卷－文6）设集合A={xx<4},B={xx²－4x+3>0}, 则集合{xx∈A且=　　　　　   .

14．（2003年高考广东卷13）不等式的解集是　　　　　　　　

15．（2003年高考北京卷－理14）将长度为1的铁丝分成两段，分别围成一个正方形

和一个圆形，要使正方形与圆的面积之和最小，正方形的周长应为　　　　　　　　　　　 .

16．（2003年高考上海卷－理11）已知点其中n为正整数.设S_n表示△ABC外接圆的面积，则=　　　　　   .

17．（2003年高考全国卷－文19）（本小题满分12分）

　　　 已知数列满足

　　　 （I）求

　　　 （II）证明

（I）解∵

（II）证明：由已知

　　 

　　　　 =

　　　 　　所以

18．（2003年高考上海卷－理19）（本题满分14分）本题共有2个小题，第1小题满分5分，第2小题满分9分.

　　已知数列（n为正整数）是首项是a₁，公比为q的等比数列.

　 （1）求和：

　 （2）由（1）的结果归纳概括出关于正整数n的一个结论，并加以证明.

[解]（1）

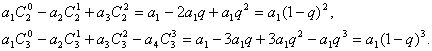
　 （2）归纳概括的结论为：

若数列是首项为a₁，公比为q的等比数列，则

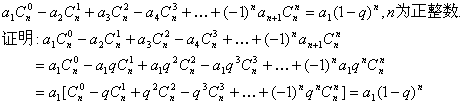
19．（2003年高考天津卷－理19）（本小题满分12分）

　　设，求函数的单调区间.

本小题主要考查导数的概念和计算，应用导数研究函数性质的方法及推理和运算能力. 满分12分.

解：.

当时　 .

（i）当时，对所有，有.

即，此时在内单调递增.

（ii）当时，对，有，

即，此时在（0，1）内单调递增，又知函数在x=1处连续，因此，

函数在（0，+）内单调递增

（iii）当时，令，即.

解得.

20．（2003年高考全国卷－理19）（本小题满分12分）

已知　设

P：函数在R上单调递减.

Q：不等式的解集为R，如果P和Q有且仅有一个正确，求的取值范围.

解：函数在R上单调递减

不等式

21．某商场预计全年分批购入每台价值为2000元的电视机共3600台。每批都购入x台，且每批均需付运费400元；贮存购入的电视机全年所付保管费与每批购入电视机的总价值（不含运费）成正比；若每批购入400台，则全年需用去运输和保管总费用43600元。现在全年只有24000元资金可以用于支付这笔费用。请问：能否恰当安排每批进货的数量使资金够用。写出你的结论，并说明理由。

解：设每批购入x台，由题意，全年需用保管费为元；设全年运输和保管总费用为y元，则

。

由已知当时，，代入上式解之得

，令，解之得（台）

将（台）代入，（元）

结果说明，只有安排每批进货120台，才能使所购资金够用。

22．（2003年高考江苏卷21）（本小题满分12分）

　　已知为正整数.

　 （Ⅰ）设；

　 （Ⅱ）设

本小题主要考查导数、不等式证明等知识，考查综合运用所数学知识解决问题的能力，满分12分.

证明：（Ⅰ）因为，

所以

（Ⅱ）对函数求导数:

∴

　　　　　 

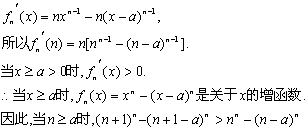
即对任意