高考数学模拟试题（新课程卷）

高考数学模拟试题（新课程卷）

 

一、选择题（本大题共１２小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1.向量=（cosα,sinα,=(cosβ,sinβ),其中α=β+，则与+的夹角为　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　 A、　　　　　　 B、　　　　　　C、　　　　　 D、

2.设f(x)的定义域为R，a、b是两个常数且b>a，如果对于任何x∈R均有f(x+a)=f(x+b)，那么对于任何x∈R,n∈Z，均有f(x)=　　  　　　　　　　　　　　　　　　(　　)

　 A、f[x+n(a+b)]　　　 B、f[x－n(a+b)]

　 C、f[x－n(a－b)]　　 D、f(x)－n(a－b)

3.已知f(x)=，函数y=g(x)的图象与y=f^－1(x+1)的图象关于直线y=x对称，则g(3)等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

　 A、3　　 　　　 B、　　　　　 　C、　　　　 　 D、

4.集合M={(x,y)y=－}，N={(x,y)y=kx－3k+1},若M∩N≠Ф,则k的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

　 A、[0，1]　　 B、[0，]　　 C、[，1]　　　D、[，]

5.设a=cos6°－sin6°,b=,c=,则有　　　　 （ 　 ）

　 A、a<b<c　　　 B、a<c<b　　　 C、a>c>b　　　　D、a>b>c

6.一个简单多面体的面有三角形和八边形两种，其顶点有24个，每个顶点处有3条棱，那么该多面体的面中三角形和八边形的数目分别是　　　　　　　　　　　　　 （　　）

　 A、8，10　　 B、10，8　　　C、8，6　　　D、6，8

7.若点F₁、F₂为椭圆+y²=1的焦点，P为椭圆上的点，且△F₁PF₂的面积为1时，·的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A、0　　　　　B、3　　　　　C、－　　 　　 D、－

8.已知球面上A、B、C三点的截面和球心的距离等于球半径的一半，且AB=BC=CA=3，则球面的面积是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A、4π　　　　  B、8π　　　　  C、12π　　　　  D、16π

9.已知等差数列{a_n}的前n项和为18，前三项和S₃=1，a_n-2+a_n-1+a_n=3，则n的值是  (　　)

A、9　　　　 B、21　　　 　　C、27　　　 　　D、30

10.如果命题“非p或非q”是假命题，则在下列各结论中，正确为　　　　　   （　　）

　　①命题“p且q”是真命题　　 ②命题“p且q”是假命题

③命题“p或q”是真命题　　 ④命题“p或q”是假命题

A、①③　　　　B、②④　　　　  C、②③　　　　D、①④

11.已知t∈R^*，由不等式x+≥2,x+=++≥3,…启发我们可推广为x+≥n+1，则t的值为　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

2

·

　　A、2ⁿ　　　 　　B、2^2(n-1)　　　　　 C、n²　　 　　　D、nⁿ

1

·

4

·

12.如图所示，在A、B间有四个焊接点，若焊接点

·

脱落，则可能导致电路不通。今发现A、B之间  A　　　　　　　　　　 B

3

线路不通，则焊接点脱落的不同情况有　　　　  　　　　　　　　　　 （　 ）

A、15　 　　　　B、13　　　　  C、12　　　　  D、10

二、填空题（本大题共4小题，每小题4分，共16分。把答案填在题中横线上）

13.函数y=2x³―3x²―12x+14的递减区间是_________________.

14.直线y=x+1与椭圆mx²+ny²=1(m>n>0)相交于A、B两点，若弦AB的中点的横坐标等于－，则双曲线－=1的两条渐近线所夹锐角的正切值为_________.

15.已知△ABC中，有A、B、C所对的边分别为a、b、c，若a=1，∠B=45°，△ABC的面积S=2，那么△ABC的外接圆的直径等于_________.

16.下列四个命题：

①a+b≥2；　　　　　　 ②sin²x+≥4；

③设x、y∈R⁺，若+=1，则x+y的最小值是12；

④若x－2<q，y－2<q，则x－y<2q

　其中所有真命题的序号是______________.

三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）

17、（本小题满分12分）

  已知向量=(cosα,sinα), =(cosβ,sinβ)

 (1)若k+=－k，求正数k的取值范围；

 (2)在(1)的条件下，设向量与向量的夹角为θ，求函数f(θ)= 的值域。

18、（本小题满分12分）

已知某种类型的高射炮在它们控制的区域内击中敌机的概率是20%，

(1)若有5门这种高射炮控制这个区域，求敌机进入这个区域后被击中的概率；

(2)要使敌机一旦进入这个区域后有90%以上的概率被击中，须至少布置几门高射炮？

　

19、（本小题满分12分）

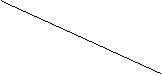
如图，在四棱锥P—ABCD中，PA、AB、AD

P

E

D

A

两两互相垂直，AB∥CD，且AB=1，AD=CD=2，

C

E是PC的中点

　(1)求证：BE∥平面PAD；

　(2)当平面PCD与平面ABCD成多大角时，

BE⊥平面PCD；

B

　(3)当平面PBC与平面PAD所成的角为45°时，

求四棱锥P—ABCD的体积。

20、（本小题满分12分）

已知函数f(x)=a₀+a₁x+a₂x²+a₃x³+…+a_nxⁿ(n∈N^*)，且y=f(x)的图象经过点

（1，n²），数列{a_n}（n∈N^*）为等差数列。

(1)求数列{a_n}的通项公式；

(2)当n为奇数时，设g(x)=[f(x)－f(－x)]，是否存在自然数m和M，使不等式m<g()<M恒成立，若存在，求出M－m的最小值；若不存在，说明理由。

21、（本小题满分12分）

如图，ADB为半圆，AB为半圆直径，O为半圆圆心，且OD⊥AB，线段OD的中垂线与半圆交于E、F两点，已知AB=4，曲线C过E点，动点P在曲线C上运动且保持PA－PB的值不变。

　 (1)建立适当的平面直角坐标系，　　　　　　　　　　　  D

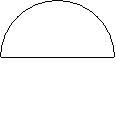求曲线C的方程；

　 (2)过D点的直线与曲线C相交　　　　 　　　 E　　　　　　　　 F

O

于不同的两点M、N，且=3，　　　　　　  A　　　　　　　　 B

求直线的方程。

22、(本小题满分14分)

设f(x)是定义在[－1，1]上的偶函数，g(x)的图象与f(x)的图象关于直线x=1对称，且x∈[2,3]时，g(x)=2a(x―2)―4(x―2)³

(1)求f(x)的表达式；

(2)若f(x)在[0，1]上是增函数，求a的取值范围；

(3)是否存在正整数a，使函数f(x)的图象的最高点落在直线y=12上？

　 若存在，试求出a的值；若不存在，请说明理由。

高考数学模拟试题答案（新课程卷）

 

一、选择题

1.B, 2.C, 3.B, 4.D, 5.A, 6.C, 7.A, 8.D, 9.C, 10.A, 11.D, 12.B

二、填空题

13.(－1,2), 14., 15.5, 16.②④

三、解答题

17.解：(1)将k+=－k两边平方，并化简整理得：·=

即cos(α－β)= 　　　　 ∵－1≤cos(α－β)≤1

∴由－1≤≤1 解得正数k的取值范围是[2－，2+]

(2)由(1)知 cosθ==·==（k+）≥

　 又0≤θ≤π，　　　 故0≤θ≤

　 从而f(θ)= =sinθ+cosθ=sin(θ+) ∈[1,]

　 即原函数的值域为[1，].

18.解：(1)设一门炮击中飞机为事件A，这五门高射炮都未击中敌机的事件记为，则P()=[P()]⁵=[1―P(A)]⁵=(1―20%)⁵=≈0.33

　　　　因此，敌机被击中的概率是P(C)=1―P()≈1―0.33=0.67

(2)设至少需布置n门高射炮才能有90%以上的概率击中敌机，现设这n门高射炮射击下敌机被击中的事件是E，则

　P()=[P()]ⁿ=[1－P(A)]ⁿ=()ⁿ

　∴P(E)=1―P()=1―()ⁿ>90%　　　　  即()ⁿ<

即8ⁿ<10^n-1　　　　　　  两边取对数得 nlg8<n―1

∴n>=≈10.3　　　故得 n≥11

即至少要布置11门高射炮

19.(1)证：取PD的中点F，连结AF、EF

　　　　 ∵E为PC的中点  ∴EF　 CD

C

又∵AB　CD　　　　 ∴AB　 EF

E

D

A

P

F

H

B

∴BE∥AF　　　　 而AF平面PAD

∴BE∥平面PAD.

　(2)解：当平面PCD与平面ABCD成45°角时，

　　　　  BE⊥平面PCD，∵PA⊥AD，PA⊥AB，

∴PA⊥平面ABCD

　　　　 ∵AB∥CD，AB⊥AD，∴CD⊥AD，

G

∴CD⊥PD

　　　　 ∴∠PDA为平面PCD与平面ABCD所成

二面角的平面角

　　　　 则∠PDA=45°　　 ∴Rt△PAD为等腰Rt△，　　∴AF⊥PD

　　　　 又CD⊥平面PAD　　　 ∴AF⊥CD　　　 ∴AF⊥平面PCD

　　　　 ∵BE∥AF　　　　　  ∴BE⊥平面PCD

　(3)解：延长DA、CB，相交于点G，则PG=平面PBC∩平面PAD

　　　　 过D作DH⊥PG于H，　连结CH　　　 ∵CD⊥平面PAD

　　　　 ∴CH⊥PG，　 ∴∠CHD为平面PBC与平面PAD所成二面角的平面角

　　　　 即∠CHD=45°　　 ∴DH=CD=2，　　　　又DG=2AD=4

　　　　 ∴∠DGH=30°　　在Rt△PAG中，PA=AG·tan30°=2·=

　　　　 ∴V_P-ABCD=××（AB+CD）×AD×PA=

20．解：(1)f(1)=n²　　　　　　　　 ∴a₀+a₁+…+a_n=n²

　　　　　  a₀+a₁=1²  　　a₁=1－a₀

　　　∴　　a₀+a₁+a₂=2²　　　　　　 ∴　 a₂=3

a₀+a₁+a₂+a₃=3²  　　　　　　　 a₃=5

　　　　设{a_n}的公差为d，则d=a₃―a₂=2，　　 ∴a₁=a₂―d=3―2=1

　　　　∴a_n=1+(n―1)×2=2n－1.

(2)n为奇数时，f(―x)=a₀―a₁x+a₂x²―a₃x³+…+a_n-1x^n-1―a_nxⁿ

　 ∴g(x)=[f(x)―f(―x)]=a₁x+a₃x³+a₅x⁵+…+a_n-2x^n-2+a_nxⁿ

∴g()=1×+5×()³+9×()⁵+…+(2n－5)×()^n-2+(2n－1)×()ⁿ　　①

∴g()=1×()³+5×()⁵+…+(2n―9)×()^n-2+(2n―5)×()ⁿ

+(2n－1)×()ⁿ⁺² ②

①　　 －②，得

g()=1×+4×[()³+()⁵+…+()^n-2+()ⁿ]―(2n―1)×()ⁿ⁺²

∴g()=―×()ⁿ―n×()ⁿ

设C_n=n×()ⁿ　　　则C_n+1―C_n=×()ⁿ×≤0

∴C_n+1≤C_n,　　　　又∵×()ⁿ随n增大而减小

∵n=1时，g()=；而―×()ⁿ―×n×()ⁿ<

∴≤g()<,∴使m<g()<M恒成立的自然数m的最大值为0,

  M的最小值为2，　　　 ∴M―m的最小值为2.

21.

D

解：(1)以直线AB、OD所在直线分别为x轴、

y轴，建立如图所示直角坐标系，则

E

F

A(－2，0)，B（2，0），E（－，1）

x

M

B

A

O

∵PA－PB=EA－EB=2<AB=4

∴曲线C为以原点为中心，A、B为焦点的

双曲线

则a=，c=2，　　∴b=

∴曲线C的方程为－=1　即x²－y²=2.

　(2)设曲线的方程为y=kx+2,代入x²－y²=2

得(k²―1)x²+4kx+6=0

△=(4k)²―4×6×(k²―1)>0，　　  解得k²<3

由=3，可知M、N在同一支上，且=3

设M(x₁,y₁),N(x₂,y₂) , ∴=3　即x₂=3x₁

由韦达定理得　　x₁+x₂=　　 

x₁x₂=>0　　　　∴1<k²<3

将x₂=3x₁代入上式，得　　4x₁=

　　　　　　　　　　　  3x₁²=　 　∴k=±

∴所求直线的方程为y=±x+2.

22.解：(1)当―1≤x≤0，2≤2－x≤3，　f(x)=g(2－x)=－2ax+4x³

　　　 当0<x≤1时，－1≤－x<0，　∴f(x)=f(－x)=2ax－4x³

　　 ∴f(x)=　　―2ax+4x³　(―1≤x≤0)

2ax―4x³　 (0<x≤１)

　　　　(2)由题意知f’(x)>０在[０，１]上恒成立，即2a－12x²>0恒成立

　　　　　 a>6x²,　　　(6x²)_max=6,　　∴a≥6.　　即a的取值范围为[6，+∞

　　　　(3)由偶函数知，只要研究函数f(x)=2ax―4x³在区间[0，1]上的最大值，

由f’(x)=2a―12x²=0，得x=

若∈（0，1 ，即0<a≤6，

则f(x)_max=f()=2a－4()³<2a≤12

故此时不存在a适合题意;

若>1，即a>6，则f(x)=2ax－4x³在区间[0，1]上为增函数

故f(x)_max=f(1)=2a－4　　　 令2a―4=12　　　得a=8

∴存在a=8，适合题意.