高考数学模拟试题
一. 选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 已知直线
：
与直线
：
平行，则实数
的值是
A. 
或2 B. 0或1 C. D. 2
2. 若复数
，则
为
A. 
B. 
C. 
D. 
3. 若
是偶函数，当
时，
，则
的解集是
A. 
B. 
C. 
D. 
4. 已知点P（
，
）在第一象限，且
，则
的取值范围是
A. 
B. 
C. 
D. 
5. 集合
与
之间的关系是
A. 
B. 
C. 
D. 
6. 已知直线
：
（
为参数）与直线
相交于点P，则点P与点A（2，）的距离为
A. 
B. 
C. 2 D. 10
7. 正三棱锥的侧面都是直角三角形，侧棱与底面所成的角为，则等于
A. 
B. 
C. 
D. 
8. 已知圆锥的母线长为4，若过圆锥顶点的所有截面面积的取值范围是（0，
］，则该圆锥的侧面展开图扇形的圆心角为
A. 
B. 
C. 
D. 或
9. 若函数的最小正周期是2T，且
对一切实数
均成立，则函数为
A. 偶函数 B. 奇函数 C. 非奇非偶函数 D. 既是奇函数又是偶函数
10. 若幂函数
满足
，那么函数
的图象为
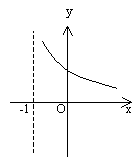
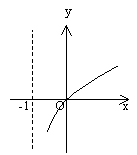
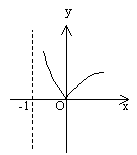
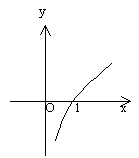
A B C D
11. 在一次足球预选赛中，某小组共有5个球队进行双循环赛（每两队之间赛两场），已知胜一场得3分，平一场得1分，负一场得0分。积分多的前两名可出线（积分相等则要比净胜球数或进球总数）。赛完后一个队的积分可出现的不同情况种数为
A. 22 B. 23 C. 24 D. 25
12. 某企业去年销售收入1000万元，年成本分为年生产成本500万元与年广告费成本200万元两部分。若利润的P％为国税，且年广告费超出年销售收入2％的部分也必须按P％征国税。已知该企业去年共纳税120万元，则税率P％为
A. 10％ B. 12％ C. 25％ D. 40％
二. 填空题：本大题共4小题，每小题4分，共16分，把答案填在题中的横线上。
13. 函数
的反函数
的定义域是______。
14. 若焦点为F的椭圆
（
为参数）内有一点P（2，1），M为椭圆上一点，则
的最小值为______。
15. 
展开式中含
项的系数是_______。
16. 若
，
，则
的值为________。
三. 解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。
17. （本小题满分12分）
在
中，
分别为角A、B、C的对边，
。
（1）求角A的度数；
（2）若
，
，求
和
的值。
18. （本小题满分12分）
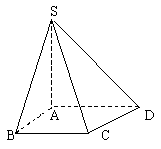
如图，直角梯形ABCD中，
，BC//AD，
平面ABCD，且
，
（1）求证：平面
平面SAC
（2）求点A到平面SCD的距离
（3）求二面角
的大小
（4）求直线SD与AC所成的角
19. （本小题满分12分）
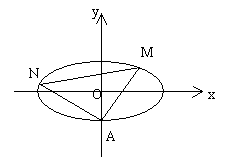
如图，若椭圆的中心在原点，焦点在轴上，一个顶点为A（0，1），且右焦点到右准线的距离为
。试问能否找到一条斜率为
（
）的直线，使与已知椭圆交于不同两点M、N，且满足
，这样的直线若不存在，说明理由；若存在，求出
的范围。
20. （本小题满分12分）
某食品厂定期购买面粉，已知该厂每天需用面粉6吨，每吨面粉的价格为1800元，面粉的保管等其它费用平均每吨每天3元，购面粉每次需支付运费900元。
（1）求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？
（2）若提供面粉的公司规定：当一次购买面粉不少于210吨时，其价格可享受9折优惠（即原价的90％），问该厂是否考虑利用此优惠条件？请说明理由。
21. （本小题满分12分）
设
（
为常数），方程
的两个实数根为
，
，且满足
，
（1）求证：
（2）设
，比较
与的大小
22. （本小题满分14分）等差数列
中，
，
是它的前
项之和，等比数列
中，公比
满足
，
是它的前项之和，若
，
，又
（1）求和的通项公式；
（2）若将数列的项重新组合成新数列
，具体法则如下：
，
，
，
，……，求
的表达式。
（3）令
，求证：
（
）
高考模拟试题答案
一. 选择题
CBAAC DCCAC CC
二. 填空题
13. （0，
） 14. 3 15. 13 16. 
三. 解答题：
17. （1）由及
得
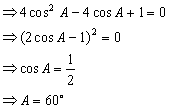
（2）由余弦定理得
又
将，代入上式，得
联解
或
18. （1）证明：由
得
，
则
又
，知
平面SAC
所以平面DSC
平面SAC
（2）过A作
，E为垂足，则
平面SCD，
，即A到平面SCD距离为
（3）作
于F，则
，
为二面角A－SD－C的平面角
又
，
则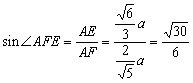
所以，二面角A－SD－C为
（4）延长BC到G，使
，则四边形ACGD为平行四边形，
为SD与AC所成的角（或补角）
，
所以SD与AC所成的角为
19. 由题意，可设椭圆为
由
即
有
得
，
故椭圆方程为
设以A（0，）为圆心，
为半径的圆的方程为
与椭圆方程联立，消去，得
（1）
假设存在斜率不为0的直线与椭圆交于不同两点M、N，且有，等价于圆A与椭圆有3个或4个交点，也等价于方程（1）在（，1］上有两个不等实根
设
在（，1］上有两个不等根的充要条件是：
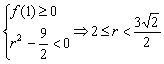
所以直线存在，的范围为［2，
）
20. （1）设该厂应每隔天购买一次面粉，其购买量为
吨，由题意知面粉的保管等其它费用为
设平均每天所支付的总费用为
元，则
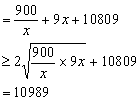
当且仅当
，
时取等号
即该厂应每隔10天购买一次面粉，才能使平均每天所支付的总费用最少。
（2）若厂家利用此优惠条件，则至少每隔35天购买一次面粉。
设该厂利用此优惠条件后，每隔（
）天购买一次面粉，平均每天支付的总费用为
元，则
令
，
则
由，知
，
则
即
，当时为增函数
又当
时，取得最小值10060.7，显然10060.7
10989
所以该厂应接受此优惠条件
21. （1）方程，即
知
，
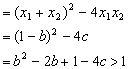
即
（2）
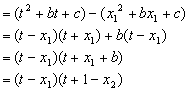
因为
所以
又
所以
故
所以有
22. （1）设的公差为
，的公比为，依题意有：
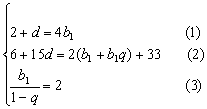
由（1）（2）（3）可化为
解得
（
与矛盾，故舍去）
再由（1）（3）可解得
，
由此，可得
，
（2）由的构成法则可知，应等于中的项之和，其第一项的项数为
，即这一项为：
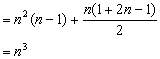
（3）由（2）得 
由（1）得：
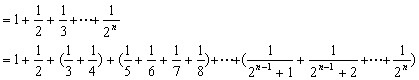
