高三数学测试题(3)
一、填空题（满分48分）
1．已知函数
，则
________.
2．设平面
与向量
垂直，平面
与向量
垂直，则平面与位置
关系是___________.
3．当
时，关于
的不等式
的解集是
.
4．若函数
的图象不经过第二象限，则
满足的条件是
.
5．若
，则
被8除所得的余数是____ __.
6．给定极限
，则极限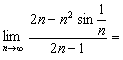
________.
7．设异面直线
、
所成的角为
，经过空间一点
有且只有一条直线
与异面直线、成
等角
，则的值为_________.
8．一块三角形菜地一面倚墙，两面需用栅栏围成,已知栅栏总长为10米,围成的三角形菜地的最
大面积等于_________平方米.
9．若①
,②
,③
,则同时满足①②③的有_______组.
10．空间不共面的四点
依次到平面的距离之比是
，则满足条件的平面的个数为________个.
11．将红、黄、绿三种不同的颜色均涂入图中五个区域中，
每个区域涂一种颜色，且相邻的区域不能涂同一种颜色，
不同的涂色方法共有_________种. （三种颜色必须用全，以数字作答）
12．平面内，若三条射线
、
、
两两成等角为
，则
。类比该特性：在空间，
若四条射线、、、
两两成等角为
，则
___________.
二、选择题（满分16分）
13．在
中，若
，则的形状一定是( )
（
）等腰三角形 （
）直角三角形 （
）等边三角形 (
)等腰直角三角形
14．若一个四面体的棱长为1或2，则这样的四面体的个数( )
（）2 （）3 （）4
() 5
15．若不等式
的解集为
，则不等式
的解
集为( )
（）
（）
（）
() 
16．设
是等差数列，
是其前
项的和，且
，
，则下列结
论错误的是 ( )
（）
（）
（）
()
与
是的最大值
三、解答题
17．（满分12分）四棱锥
的底面
是平行四边形，
、
、
，(1) 求证：
底面；(2) 求
的长。
18．（满分12分）在实数范围内解不等式：
.并利用解此题的方法证明：
有唯一解。
19．（满分14分）已知函数
，常数
。
（1）设
，证明：函数
在
上单调递增；
（2）设
且
的定义域和值域都是
，求
的最大值。
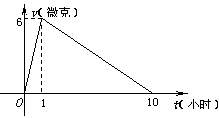
20．（满分14分）某医药研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量
与时间
之间近似满足如图所示的曲线.
（1）写出服药后与之间的函数关系式；
（2）据测定：每毫升血液中含药量不少于4微克时治疗疾病有效，假若某病人一天中第一次服药时间为早晨
，问一天中怎样安排服药的时间（共4次）效果最佳？
21．（本题满分16分）数列
与
的前项和分别是
和
，且
,
。
（1）求证：数列是从第三项起的等比数列；
（2）当数列是从第一项起的等比数列时，用的式子表示；
（3）在（2）的条件下，对于给定的自然数
，当
时, 
,
且
，试求
的值。
22．（本题满分18分）已知函数
（1）求
及
的值；
（2）是否存在自然数，使
对一切都成立，若存在，求出自然数的最小值；不存在，说明理由；
（3）利用（2）的结论来比较
和
的大小．
高三数学测试题(3)答案
一、填空题: 1．0； 2．垂直； 3．
； 4．
； 5．0或6； 6．
； 7．
或
；8．
； 9．36； 10．8； 11．42； 12．
；
二、选择题: 13—16
；
三、解答题
17．解:① 
,
,
,
,
;
② 
,
,
。
18．解：由
得
,显然
是减函数,又当
时, 
即
;当
时, 
；不等式的解集为
.
由方程
得, 
,显然函数
是减函数,又当
时，，当
时, 
,当
时, 
,方程有唯一解.
19．（1）任取
，
，且
，
， 因为
，，，所以
，即
，故
在
上单调递增。
（2）因为在上单调递增，
的定义域、值域都是
，
即
是方程
的两个不等的正根
有两个不等的正根。
所以
，
。
∴
，∴
时，
取最大值
。
20．(1)依题得，
(2)设第二次服药时在第一次服药后t1小时，则
,因而第二次服药应在11:00；
设第三次服药在第一次服药后t2小时，则此时血液中含药量应为两次服药量的和，即有
解得t2=9小时，故第三次服药应在16:00；
设第四次服药在第一次后t3小时（t3>10），则此时第一次服进的药已吸收完，此时血液中含药量应为第二、三
次的和，
解得t3=13.5小时，故第四次服药应在20:30.
21．⑴ 
，当
时，
，
，得
，即
从第三项起成等比；
⑵若从第一项起成等比，那么由
，
，得
，
，
，
；
⑶ 
，又
，
，
由已知
，
，
，
， 故
为所求。
22．（1）
；
．
（2）假设存在自然数,使
对一切
都成立.由
,
得
，当
时，不等式
显然不成立．当
时，
，当
时，显然
,当
时，
=
成立，则 
对一切
都成立．所以存在最小自然数
。
（3）． 由
（
），所以
，
，……，
，
相乘得
成立．