高三数学测试题—多面体和旋转体

高三数学测试题—多面体和旋转体

一、选择题（本题每小题5分，共60分）

1．三棱锥的三个侧面与底面所成的角都相等，则顶点在底面上的射影一定是底面三角形的

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．内心　　　　　　　　　 B．外心　　　　　　　　　 C．重心　　　　　　　　　 D．垂心

2．正三棱锥S—ABC的侧棱SA、SB、SC两两垂直，体积为V，A′、B′、C′分别是SA、

　 SB、SC上的点，且，则三棱锥S—A′B′C′的体

　 积为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　 D．

3．如果正四棱锥的侧面积等于底面积的2倍，则侧面与底面所成的角等于　　　　　　 （　　）

　　　 A．30°　　　　　　　　　 B．45°　　　　　　　　　 C．60°　　　　　　　　　 D．75°

4．把边长为4和2的一个矩形绕其一边卷成一个圆柱的侧面，则圆柱的体积为　　　（　　）

　　　 A．16π　　　　　　　　　 B．8π　　　　　　　　　　 C．16π或8π　　　　 D．16π或32π

5．正四棱台的上、下底面边长分别为1cm，3cm，侧棱长为2cm，则棱台的侧面积为（　　）

　　　 A．　　　　　　　　　B．　　　　　　　　　C．　　　　　　　　　D．

6．圆台上、下底面边长分别为1和7，作与两底平行的截面，且截面与上、下两底距离之比

　 为1∶2，则截面的面积为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　　D．

7．圆锥的顶角为120°，高为a，用过顶点的截面去截圆锥，则截面的最大面积为（　　）

　　　 A．a²　　　　　　　　　　　 B．2a²　　　　　　　　　　 C．　　　　　　　　 D．4a²

8．若四棱锥P—ABCD的底面是边长为a的正方形，侧棱PA=a，PB=PD=，则在它的

　 五个面中，互相垂直的面共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．3对　　　　　　　　　　B．4对　　　　　　　　　　C．5对　　　　　　　　　　D．6对

9．已知：圆柱的底面半径为1，高为4，则它的内接正三棱柱的体积等于　　　　　　　（　　）

　　　 A．　　　　　　　　 B．2　　　　　　　　　C．3　　　　　　　　　D．4

10．一个正四面体外切于球O₁，同时内接于球O₂，则球O₁与球O₂的体积之比为（　　）

　　　 A．1∶27　　　　　　　　 B．1∶6　　　　　　 C．1∶8　　　　　　　　　 D．1∶3

11．三棱锥的三条侧棱两两垂直，其长分别是1，，则此三棱锥的外接球面积是（　　）

　　　 A．6π　　　　　　　　　　 B．12π　　　　　　　　　 C．18π　　　　　　　　　 D．24π

12．三棱柱ABC—A₁B₁C₁的体积为1，P是侧棱BB₁上的一点，则四棱锥P—ACC₁A₁的体

积是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　　D．

二、填空题（本题每小题4分，共16分）

13．正四面体的棱长为a，对棱之距为b，则=　　　　　 .

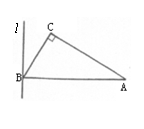
14．如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4，直线l

与平面△ABC在同一平面内，且过B点，l⊥AB，△ABC绕直

线l旋转一周所得几何体的体积为　　　　　　  .

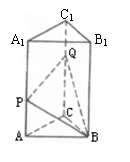
15．如图，直三棱柱ABC—A₁B₁C₁的体积为V，P、Q分别是侧棱AA₁、

CC₁上的点，且AP=C₁Q，则四棱锥B—APQC的体积为　　　　 .

16．圆台母线与底面成α角，半径为R的球内切于圆台，则球面被圆台

分成的两部分面积之比是　　　　　  .

三、解答题

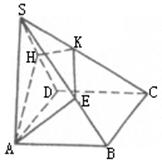
17．（本题满分12分）如图，四棱锥ABCD的底面是正方形，侧棱SA⊥底面ABCD，截面

AEKH⊥SC.求证：E、H在以AK为直径的圆上.

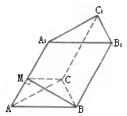
18．（本题满分12分）斜三棱柱ABC—A₁B₁C₁的底面是边长为a的正三角形，侧棱长为b，

侧棱AA₁和AB、AC都成45°的角，求棱柱的侧面积和体积.

19．（本题满分12分）如图在四面体ABCD中，AB=AC=AD=2a，且AB、AC、AD两两互

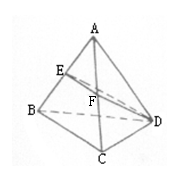相垂直，E、F分别是AB、AC的中点.求平面BCD与平面EFD所成二面角的正切值.

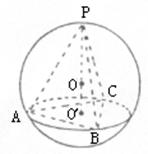
20．（本题满分12分）过半径为R的球面上一点P引三条长度相等的弦PA、PB、PC，它们

间两两夹角相等.（Ⅰ）若∠APB=2α，求弦长：（Ⅱ）求三棱锥P—ABC体积的最大值.

21．（本题满分12分）圆锥底面半径为R，母线与底面夹角为2α，第一个球与圆锥底面和

侧面都相切，第二个球与第一个球和圆锥侧面都相切，如此继续下去，当这些球的个数

无限增多时，求所有球的体积之和.

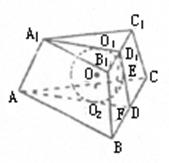
22．（本题满分14分）正三棱台有一内切球，若内切球的面积与这棱台的全面积之比为

∶39，求棱台的侧面与底面所成角的大小.

高三数学测试题参考答案

十一、多面体和旋转体

一、1.A　 2.C 　3.C 　4.D 　5.D 　6.C 　7.B 　8.B 　9.C 　10.A   11.A　12.B

二、13． ； 14．  ； 15． ； 16．

三、17．（1）证明：∵SA⊥底面ABCD，底面ABCD是正方形，∴BC⊥侧面SAB，AE侧面SAB，

∴AE⊥BC，又∵SC⊥截面AEKH. ∴AE⊥SC，∴AE⊥侧面SBC，∴AE⊥KE，同理AH⊥HK.

∴A、E、K、H四点共同，且AK是圆的直径.

18．解：如图，过B作BM⊥AA₁，垂足为M，连结CM. ∵侧棱AA₁和

AB、AC都成45°，∴△AMB≌△CMA，∴CM⊥AA₁，于是截面

MBC是斜三棱柱的直截面.由已知.

∴斜棱柱的侧面积

19．解：∵E、F分别是AB、AC的中点，∴EF∥底面BCD.设平面EFD∩平面BCD=l，取EF、BC的中点

分别为M、N，连结DM、DN.∵AB=AC=AD=2a，且AB、AC、AD两两重直，∴BC=CD=BD=，

DE=DF=，且DM⊥EF，DN⊥BC. 又∵EF∥BC∥l，∴DM⊥l，DN⊥l. ∴∠MDN就是平面BCD

与平面EFD所成二面角的平面角.　在△MND中，，

. 连结AN，则AN必过M且

　

20．（1）如图（见题图），由PA=PB=PC，且∠APB=∠BPC=∠CPA，知三棱锥P—ABC是一个正三棱锥，

作其高PO′则O′为正△ABC的中心，显然球心O也在PO′所在的直线上.

设且

又　①

又∵过PO′与PB的平面截球的截面为球的大圆，延长PO′交球面于Q，则PB⊥BQ.

　②　把②代入①消去h，整理得

，

此即为所求的弦PA、PB、PC的长.

（2），

　

当且仅当 即时取等号. ∴当圆锥的高等于时，其体积取得最大值

21．解：作出满足题条件的轴截面图形（如图），圆锥的高SO通过球心O₁、O₂、O₃…，设它们与圆锥侧面

相切的切点分别是E、F、G….球的半径分别是r₁、r₂、r₃….于是便有：r₁=Rtgα，在Rt△SO₂F中，

r₂=SO₂cos2α，又∵SO₂=SO－OO₂=Rtg2α－2r₁－r₂，∴r₂=（R·tg2α－2Rtgα－r₂）·cos2α，

∴r₂=Rtg³α. 同理r₃=Rtg⁵α…　∴

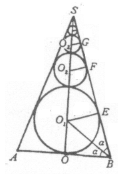
22．解：如图，球O内切于三

棱台ABC—A₁B₁C₁，O₁、

O₂为棱台上下底面中心，

O₁、O、O₂三点共线，过

22题图

21题图

A₁A、O₁O作截面交B₁C₁BC

于D₁、D，则球的大圆O切

AD、D₁D、A₁D₁于O₂、E，O₁，设棱台上、下底面边长分为a、b，则O₁D₁=，

，过D₁作D₁F⊥O₂D于F，则　

　设棱台的侧面与底面所成

的角为α，则

.

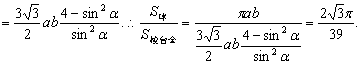
，由此解得.

即棱台的侧面与底面所成的角为60°