高三教学情况调查测试数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)
参考公式
|
|
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把所选项前的字母填在题后括号内.
1.直线![]() 的倾斜角所在的区间是 ( )
的倾斜角所在的区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.不等式![]() 的解集为 ( )
的解集为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知θ是锐角,那么下列各值中![]() 能取到的值是 ( )
能取到的值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.已知等差数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() 等于 ( )
等于 ( )
A.18 B.36 C.54 D.72
6.已知二面角![]() 的大小为60°,b和c是两条异面直线,则在下列四个条件中,能
的大小为60°,b和c是两条异面直线,则在下列四个条件中,能
使b和c所成的角为60°的是 ( )
A.b∥![]() ,c∥
,c∥![]() B.b∥
B.b∥![]() ,c⊥
,c⊥![]()
C.b⊥![]() ,c⊥
,c⊥![]() D.b⊥
D.b⊥![]() ,c∥
,c∥![]()
7.设F1,F2是双曲线![]() 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且![]() =0,则
=0,则
![]() 的值等于 ( )
的值等于 ( )
A.2 B.![]() C.4 D.8
C.4 D.8
8.过点(1,3)作直线l,若l经过点(a,0)和(0,b),且![]() ,则可作出的l的条数
,则可作出的l的条数
为 ( )
A.1 B.2 C.3 D.多于3
9.已知![]() ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )
A.函数![]() 的周期为2π
的周期为2π
B.函数![]() 的最大值为1
的最大值为1
C.将![]() 的图象向左平移
的图象向左平移![]() 单位后得
单位后得![]() 的图象
的图象
D.将![]() 的图象向右平移
的图象向右平移![]() 单位后得
单位后得![]() 的图象
的图象
10.从装有4粒大小、形状相同,颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球
(至少一粒),则倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率 ( )
A.小 B.大 C.相等 D.大小不能确定
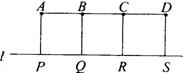
|
路,图中所标线段为道路, ABQP、BCRQ、CDSR近似
于正方形.已知A、B、C、D 四个采煤点每天的采煤量之
比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量
都成正比.现要从P、Q、R、S中选出一处设立一个运煤中
转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在 ( )
A.P点 B.Q点 C.R点 D.S点
|
①![]() ; ②
; ②![]() ;
;
③![]() ④
④![]()
其中正确结论的个数是 ( )
A.1 B.2
C.3 D.4
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共有4小题,每小题4分,共16分.把答案填在题中横线上.
13.抛物线![]() 的准线方程是
.
的准线方程是
.
14.已知![]() 是偶函数,当
是偶函数,当![]() 的最大值为
的最大值为
m,最小值为n,则m-n= .
15.为了科学地比较考试的成绩,有些选拔性考试常常会将考试分数转化为标准分,转化关
系式为:![]() (其中x是某位学生的考试分数,
(其中x是某位学生的考试分数,![]() 是该次考试的平均分,s是该次
是该次考试的平均分,s是该次
考试的标准差,Z称为这位学生的标准分).转化成标准分后可能出现小数和负值,因此,
又常常再将Z分数作线性变换转化成其他分数. 例如某次学业选拔考试采用的是T分
数,线性变换公式是:T=40Z+60. 已知在这次考试中某位考生的考试分数是85,这次考
试的平均分是70,标准差是25,则该考生的T分数为 .
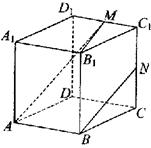
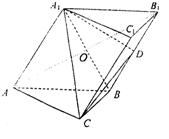
|
个结论:
①直线AM与CC1是相交直线
②直线AM与NB是平行直线
③直线BN与MB1是异面直线
④直线AM与DD1是异面直线
其中正确的结论为 (注:把你认为正确的结论的序号都填上)
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角均为120°.(Ⅰ)求证:(a-b)⊥c; (Ⅱ)若(ka+b+c)>1(k∈R),求k的取值范围.
18.(本小题满分12分)
某种电路开关闭合后,会出现红灯或绿灯闪动,已知开关第一次闭合后,出现红灯和出现绿灯的概率都是![]() .从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是
.从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是![]() ,出现绿灯的概率是
,出现绿灯的概率是![]() ;若前次出现绿灯,则下一次出现红灯的概率是
;若前次出现绿灯,则下一次出现红灯的概率是![]() ,出现绿灯的概率是
,出现绿灯的概率是
![]() .问:(Ⅰ)第二次闭合后出现红灯的概率是多少?(Ⅱ)三次发光中,出现一次红灯、两次绿灯的概率是多少?
.问:(Ⅰ)第二次闭合后出现红灯的概率是多少?(Ⅱ)三次发光中,出现一次红灯、两次绿灯的概率是多少?
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分.
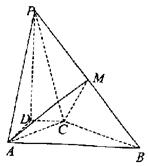
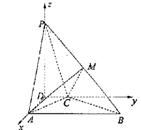
|
如图,四棱锥P—ABCD中,PD⊥平面ABCD,PA与平面
ABCD所成的角为60°,在四边形ABCD中,∠D=∠DAB=90°,
AB=4,CD=1,AD=2.
(Ⅰ)建立适当的坐标系,并写出点B、P的坐标;
(Ⅱ)求异面直线PA与BC所成的角;
(Ⅲ)若PA的中点为M,求证:平面AMC⊥平面PBC.
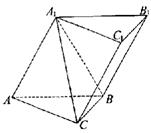
19.(乙)(本小题满分12分)
|
(Ⅰ)求证:平面CA1B⊥平面A1ABB1
(Ⅱ)求直线A1C与平面BCC1B1所成角的正切值;
(Ⅲ)求点C1到平面A1CB的距离.
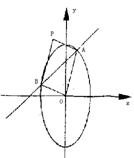
|
直线![]() 交于A、B
交于A、B
两点,以OA、OB为邻边作平行四边形OAPB(O为坐标原点).
(Ⅰ)若![]() ,且四边形OAPB为矩形,求a的值;
,且四边形OAPB为矩形,求a的值;
(Ⅱ)若![]() ,当k变化时(k∈R),求点P的轨迹方程.
,当k变化时(k∈R),求点P的轨迹方程.
21.(本小题满分12分,附加题满分4分)
某厂在一个空间容积为2000m3的密封车间内生产某种化学药品. 开始生产后,每满60分钟会一次性释放出有害气体am3,并迅速扩散到空气中.每次释放有害气体后,车间内的净化设备随即自动工作20分钟,将有害气体的含量降至该车间内原有有害气体含量的r%,然后停止工作,待下一次有害气体释放后再继续工作. 安全生产条例规定:只有当车间内的有害气体总量不超过1.25am3时才能正常进行生产.
(Ⅰ)当r=20时,该车间能否连续正常6.5小时?请说明理由;
(Ⅱ)能否找到一个大于20的数据r,使该车间能连续正常生产6.5小时?请说明理由;
(Ⅲ)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
已知该净化设备的工作方式是:在向外释放出室内混合气体(空气和有害气体)的同时向室内放入等体积的新鲜空气. 已知该净化设备的换气量是200m3/分,试证明该设备连续工作20分钟能够将有害气体含量降至原有有害气体含量的20%以下.(提示:我们可以将净化过程划分成n次,且n趋向于无穷大.)
(22)(本题满分14分)
已知![]() 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程
![]() 有三个根,它们分别为
有三个根,它们分别为![]() .(Ⅰ)求c的值;(Ⅱ)求证
.(Ⅰ)求c的值;(Ⅱ)求证![]() (Ⅲ)求
(Ⅲ)求![]() 的取值范围.
的取值范围.
高三教学情况调查测试数学试卷
参考答案及评分标准
一、选择题:本题考查基本知识和基本运算.每小题5分,满分60分.
1.B 2.C 3.A 4.A 5.D 6.C 7.A 8.B 9.D 10.B 11.B 12.C
二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分.
13.![]() 14.1 15.84 16.③④
14.1 15.84 16.③④
三、解答题
17.解(Ⅰ)![]() 且a、b、c之间的夹角均为120°,
且a、b、c之间的夹角均为120°,
![]() …3分
…3分 ![]() .…4分
.…4分
(Ⅱ)![]() ……………………………………6分
……………………………………6分
![]() …8分
…8分
![]() …10分
…10分 ![]() ……12分
……12分
18.解(Ⅰ)如果第一次出现红灯,则接着又出现红灯的概率是![]() ;………………2分
;………………2分
如果第一次出现绿灯,则接着出现红灯的概率为![]() .……………………………4分
.……………………………4分
综上,第二次出现红灯的概率为![]() +
+![]() .………………………………5分
.………………………………5分
(Ⅱ)由题意,三次发光中,出现一次红灯、两次绿灯的情况共有如下三种方式:
①当出现绿、绿、红时的概率为![]() ;……………………………………7分
;……………………………………7分
②当出现绿、红、绿时的概率为![]() ;……………………………………9分
;……………………………………9分
③当出现红、绿、绿时的概率为![]() ;…………………………………………11分
;…………………………………………11分
所以三次发光中,出现一次红灯、两次绿灯的概率为
![]() +
+![]() +
+![]() =
=![]() ………………………………………………12分
………………………………………………12分
19.(甲)解(Ⅰ)建立如图所示的空间直角坐标系![]()
∵∠D=∠DAB=90°,AB=4,CD=1,AD=2,
∴A(2,0,0),C(0,1,0),B(2,4,0).…………………………………2分
由PD⊥平面ABCD,得∠PAD为PA与平面ABCD所成的角,∴∠PAD=60°.
|
∴![]() .…………………………4分
.…………………………4分
(Ⅱ)![]()
![]() ……6分
……6分
所以PA与BC所成的角为![]() …………………7分
…………………7分
(Ⅲ)![]() .
.
![]() …………………………………8分
…………………………………8分
![]() ,
,
![]() ……………………………………………10分
……………………………………………10分
![]()
![]() .…………………………………………………………12分
.…………………………………………………………12分
19.(乙)证(Ⅰ)因为四边形BCC1B1是矩形∴BC⊥BB1,
又∵AB⊥BC,∴BC⊥平面A1ABB1,…………………………………………2分
∵BC![]() 平面CA1B,∴平面CA1B⊥平面A1ABB1.……………………………3分
平面CA1B,∴平面CA1B⊥平面A1ABB1.……………………………3分
解(Ⅱ)过A1作A1D⊥B1B于D,连接DC,∵BC⊥平面A1ABB1,∴BC⊥A1D
∴A1D⊥平面BCC1B1,故∠A1CD为直线A1C与平面BCC1B1所成的角.……5分
|
因为四边形A1ABB1是菱形,∠A1AB=60°,CB=3,
AB=4,∴![]() ,
,
![]() .………………7分
.………………7分
(Ⅲ)∵B1C1∥BC1, ∴B1C1∥平面A1BC,
∴C1到平面A1BC的距离即为B1到平面A1BC的距离.…………………………9分
连结AB1 ,AB1与A1B交于点O,∵四边形A1ABB1是菱形,∴B1O⊥A1B.
∵平面CA1B⊥平面A1ABB1,∴ B1O⊥平面A1BC
∵B1O即为C1到平面A1BC的距离.………………11分 ∵B1O=![]() ,
,
∴C1到平面A1BC的距离为![]() .………………………………………………12分
.………………………………………………12分
20.解(Ⅰ)设![]() …………2分
…………2分

![]() ,………………………………4分
,………………………………4分
![]() ……………………………………6分
……………………………………6分
(Ⅱ)设![]()
因为A、B在椭圆![]()
相减得![]() ……………………………………9分
……………………………………9分
所以 …………………………………………11分
…………………………………………11分
![]() ……………12分
……………12分
21.解(Ⅰ)∵第一次释放有害气体![]() ,∴第二次释放有害气体后(净化之前),车间内共有有害气体
,∴第二次释放有害气体后(净化之前),车间内共有有害气体![]() ,第三次释放有害气体后(净化之前),车间内共有有害气体
,第三次释放有害气体后(净化之前),车间内共有有害气体![]() ,…2分……∵6.5小时共释放出6次有害气体,且有害气体的含量逐次递增,∴要使该车间能连续正常生产,在最后一次释放有害气体后(净化之前),车间内有害气体总量不得超过1.25am3,即必须要有
,…2分……∵6.5小时共释放出6次有害气体,且有害气体的含量逐次递增,∴要使该车间能连续正常生产,在最后一次释放有害气体后(净化之前),车间内有害气体总量不得超过1.25am3,即必须要有![]() ,
,
即![]() …………4分
…………4分 ![]()
∴当r=20时,该车间能连续生产6.5小时.…………………………………6分
(Ⅱ)![]() 满足条件,即要有
满足条件,即要有![]()
即![]() (*)…8分
(*)…8分
![]()
要使(*)成立,只要![]() 即可,……………………10分
即可,……………………10分
![]() ,就可使该车间连续生产6.5小时.………………………………………………………………………12分
,就可使该车间连续生产6.5小时.………………………………………………………………………12分
(Ⅲ)设车间内原有有害气体量为A,将20分钟的净化过程划分成n次,则每次的换气量为![]() . 不防假设换气过程是先放入新鲜空气再释放混合气体,∵净化后残留的有害气体量=净化前残留的有害气体量-被释放混合气体中所含有害气体量,第一次将化后残留的有害气体量为:
. 不防假设换气过程是先放入新鲜空气再释放混合气体,∵净化后残留的有害气体量=净化前残留的有害气体量-被释放混合气体中所含有害气体量,第一次将化后残留的有害气体量为: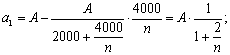
第二次净化后残留的有害气体量为: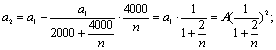
……第n次净化后残留的有害气体量为:![]() ……………………2分
……………………2分
当n极大时,可将![]() 看作整数k,
看作整数k,![]()
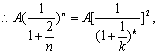
![]()
∵20分钟能够将有害气体含量降至原有有害气体含量的20%以下.……………4分
22.解(Ⅰ)![]() ………1分
………1分 ![]() 上是增函数,在[0,2]上
上是增函数,在[0,2]上
是减函数,∴当![]() 取到极大值,
取到极大值,![]() ……3分
……3分
(Ⅱ)![]() ………4分
………4分
![]() 的两个根分别为
的两个根分别为![]()
∵函数![]() 上是减函数,
上是减函数,![]() .……………………7分
.……………………7分
![]() ……………………………9分
……………………………9分
(Ⅲ)![]()
![]()
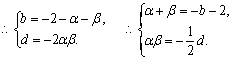 …………………………………………12分
…………………………………………12分
![]()
![]() .………………………………………………………14分
.………………………………………………………14分