高三教学质量调测
数 学
本试卷分两部分,满分150分,考试时间120分钟。
|
三角函数的和差化积公式
![]()
![]()
![]()
![]()
一、选择题:本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.![]() 的值是 ( )
的值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知集合M={![]() },N={
},N={![]() },若M∩N=N,则实数a的值是( )
},若M∩N=N,则实数a的值是( )
A.1 B.-1 C.1或-1 D.0或1或-1
3.![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件
4.两非零复数![]() 、z2分别对应向量
、z2分别对应向量![]() 、
、![]() ,若z1+z2=z1-z2,则向量
,若z1+z2=z1-z2,则向量![]() 与
与![]() 的关系 ( )
的关系 ( )
A.![]() =
=![]() B.
B.![]() =
=![]() C.
C.![]() ⊥
⊥![]() D.
D.![]() 与
与![]() 共线
共线
|
|
6.(理科做)已知两直线的极坐标方程分别为:![]() ,则两直线的位置关系是 ( )
,则两直线的位置关系是 ( )
A.平行 B.垂直 C.相交但不垂直 D.都有可能
(文科做)已知直线![]() 平行,则实数a的值等于 ( )
平行,则实数a的值等于 ( )
A.-1 B.2 C.-1或2 D.![]()
7.将长、宽分别为4、3的矩形ABCD沿对角线折成直二面角,则折后所成四面体ABCD
的体积是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.用1,2,2,3,3,3这六个数字组成的不同六位数共有 ( )
A.20个 B.60个 C.90个 D.120个
9.已知圆锥曲线C的焦点A(1,0),对应准线的方程为x=5,若点P(3,a)(a≠0)在曲
线C上,则曲线C必是 ( )
A.圆 B.椭圆 C.双曲线 D.抛物线
10.磁悬浮列车是一种科技含量很高的新型交通工具.它有速度快、爬坡能力强、能耗低的优点.它每个座位的平均能耗仅为飞机每个座位的平均能耗的三分之一、汽车每个座位的平均能耗的70%.那么汽车每个座位的平均能耗是飞机每个座位平均能耗的 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知a、b、c、d是四条直线,如果![]() ,则结论“a∥b”与“c∥d”中成立的情况是 ( )
,则结论“a∥b”与“c∥d”中成立的情况是 ( )
A.一定同时成立 B.至多一个成立 C.至少一个成立 D.可能同时不成立
12.在圆![]() 有n条弦的长度成等差数列,最小弦长为数列的首项
有n条弦的长度成等差数列,最小弦长为数列的首项
![]() ,最大弦长为
,最大弦长为![]() ,若公差
,若公差![]() ,那么n的取值集合为 ( )
,那么n的取值集合为 ( )
A.{3,4,5} B.{4,5,6} C.{3,4,5,6} D.{4,5,6,7}
二、填空题:本大题共4小题,每小题4分,共16分.
|
14.已知![]() .
.
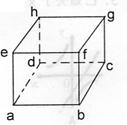
15.如图,已知正方体八个顶点标有a、b、c、d、e、f、g、h
八个数字,且每个数字是相邻3个顶点所标数字的算术平均
值,则a+b+c+d-(e+f+g+h)等于 .
16.四个命题:(1)若两直线a、b与平面α成等角,则a∥b;
(2)若一个等差数列的前m项和为30,前2m项和为80,则前3m项和为130;
(3)设![]() 为虚数单位,且
为虚数单位,且![]() ;
;
(4)已知![]() 、
、![]()
其中正确命题的序号是 .
三、解答题:共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
已知函数![]()
(1)当a=1时,求f(x)的单调递增区间;
(2)(理科做)当a<0,且x∈[0,π]时,f(x)的值域是[3,4],求a、b的值.
(文科做)当a>0,且x∈[0,π]时,f(x)的值域是[3,4],求a、b的值.
18.(本题满分12分)
解关于x的不等式:![]()
19.(本题满分12分)
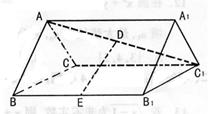
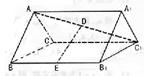
如图,在正三棱柱ABC—A1B1C1中,各棱长都相等,D、E分别为AC1、BB1的中点.
|
(2)求二面角A1—DE—B1的大小.
20.(本题满分12分)
某市为创国家级卫生城市,对旧河道清淤改造加大了力度.河道指挥部要求承包某段河道清淤任务的工程队必须在24小时内完成任务.经测算,完成工程需20辆翻斗车同时作业24小时,工程队共有25辆翻斗车,但目前只有一辆翻斗车可立即投入使用,其余的开工后每隔20分钟能有一辆翻斗车到达投入施工. 问在24小时内该工程队能否按指挥部要求完成任务?
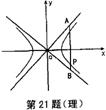
21.(本题满分12分)
|
(1)求双曲线C的渐近线方程;
(2)若AB是夹在渐近线位于一、四象限部分间的动弦,
△AOB面积为定值![]() ,且双曲线C过AB的一个三等
,且双曲线C过AB的一个三等
分点P,试确定双曲线C的方程.
(文科做)已知函数![]() 在区间(0,1)上是单调递增函数.
在区间(0,1)上是单调递增函数.
(1)求实数a的取值范围;
(2)当a取最小值时,定义数列{an}:a1=b,an+1=![]() ,求证
,求证![]()
22.(本题满分14分)
(理科做)已知函数![]() 在区间(0,1)上是单调递增函数.
在区间(0,1)上是单调递增函数.
(1)求实数a的取值范围;
(2)当a取最小值时,定义数列{an}:a1=b,an+1=![]() ,求证
,求证![]()
(3)在(2)的条件下,是否存在正实数p,使得![]() 对一切正整数n都成立?若存在则求出p的取值范围,若不存在试说明理由.
对一切正整数n都成立?若存在则求出p的取值范围,若不存在试说明理由.
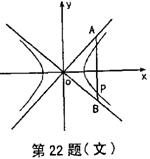
(文科做)如图,已知双曲线C的方程为![]() ,离心率为
,离心率为![]() .
.
(1)求双曲线C的渐近线方程.
(2)若AB是夹在渐近线位于一、四象限部分间的动弦,△AOB面积为定值![]() ,且 双曲线C过AB的一个三等分点P,试确定双曲线C的方程.
,且 双曲线C过AB的一个三等分点P,试确定双曲线C的方程.
|
高三教学质量调测
数学参考答案
一、ADACB B(文A)CBCC CD
二、13.3 14.-3 15.0 16.(4)
三、17.解(1)![]() …………3分
…………3分
∴递增区间为![]() …………………………………6分
…………………………………6分
(2)![]()
而![]() ……………………9分
……………………9分
(理科)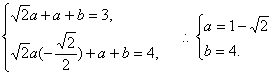 ……………………………12分
……………………………12分
(文科)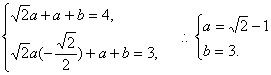 ……………………………12分
……………………………12分
18.解:![]()
![]() …4分
…4分
当![]() ……………………8分
……………………8分
当![]() ………………12分
………………12分
|
19.(1)证:取A1C1中点F,连DF,B1F1,
DF平行且等于![]() AA1, ∴DF平行且等于EB1,
AA1, ∴DF平行且等于EB1,
∴四边形DFB1E为平行四边形…………………(3分)
∴DE∥B1F ∴DE∥平面A1B1C1………………(6分)
(2)解:易知B1F⊥平面ACC1A1, ∵ED∥B1F, ED⊥平面ACC1A1,
∴ED⊥A1D1,ED⊥DF,∴∠A1DF即为所示二面角的平面角.………………9分
由已知各棱长均为a,∴A1F=DF=![]()
∴△A1DF为等腰直角三角形. ∴∠A1DF=45°∴所求二面角为45°……12分
20.解:设从第一辆车投入工作算起,各车工作时间分别为a1,a2,…a25, 组成一公差为
![]() (小时)的等差数列,只须比较当a1=24时,各车工程量之和与欲完成的工程量20×24(车小时)的大小.…………………………………………………………4分
(小时)的等差数列,只须比较当a1=24时,各车工程量之和与欲完成的工程量20×24(车小时)的大小.…………………………………………………………4分
由![]() ……………………………………7分
……………………………………7分
及![]() ……………9分
……………9分 ![]()
∴该工程队能够按指挥部要求在24小时内完成任务.……………………………12分
21.解(理科)(1)由题意知双曲线实轴在x轴上,由![]()
![]() ……………………………4分
……………………………4分
∴所求双曲线渐近线方程为![]() …………………………………………6分
…………………………………………6分
(2)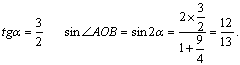
由![]()
设![]()
![]() (*)……………………………………………………………………9分
(*)……………………………………………………………………9分
设P(![]() ),由定比分点公式:
),由定比分点公式: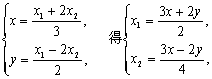
代入(*)得:![]() 即为双曲线C的方程.……………………………12分
即为双曲线C的方程.……………………………12分
(文科)(1)![]()
![]()
而![]() …6分
…6分
(2)当a=3时,![]() 下用数学归纳法证明:
下用数学归纳法证明:![]()
当n=1时,![]() ………………………………………………………………8分
………………………………………………………………8分
假设![]()
![]()
![]() 也成立.
也成立. ![]() …………………………………………………………………………12分
…………………………………………………………………………12分
22.解(理科)(1)对于![]()
![]() ………………………………………………………………2分
………………………………………………………………2分
![]()
而![]() ……5分
……5分
(2)当a=3时,![]()
下用数学归纳法证明:![]()
当n=1时,![]()
假设![]()
![]()
![]() 也成立.
也成立. ![]() …………………………………………………………………………10分
…………………………………………………………………………10分
(3)![]()
![]() 递增.……………………………………………………………12分
递增.……………………………………………………………12分
若![]() ,
,
![]() …………………………………………14分
…………………………………………14分
文科(1)由题意知双曲线实轴在x轴上,由![]()
![]() ………………………………5分
………………………………5分
∴所求双曲线渐近线方程为![]() .……………………………………………7分
.……………………………………………7分
(2)由![]()
设A![]()
![]() (*)…………………………………………………………………10分
(*)…………………………………………………………………10分
设P(x,y),由定比分点公式: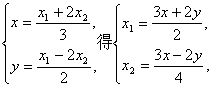
代入(*)得:![]() 即为双曲线C的方程.……………………………14分
即为双曲线C的方程.……………………………14分