高三联考数学试题
一、选择题:
1、已知方程![]() 的解为
的解为![]() ,则
,则![]() 属于(
)
属于(
)
A、(3,4) B、(4,5) C、(5,6) D、(6,7)
2、直线![]() 与圆
与圆![]() 的位置关系是( )
的位置关系是( )
A、相交 B、相离 C、相切 D、相交或相切
3、若![]() 且
且![]() ,则
,则![]() 的值为(
)
的值为(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
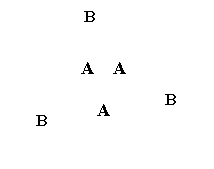
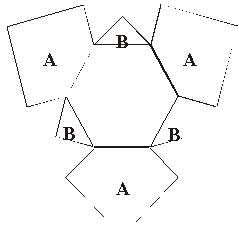
4、三个12cm×12cm的正方形都被连接两条邻边中点的直线分成A、B两片,如图(1)把6片粘在一个正六边形的外面,如图(2)然后折成多面体,如图(3)则此多面体的体积是( )
|
|
|
|
| (1) | (2) | (3) |
A、216![]() B、648
B、648![]() C、864
C、864![]() D、1728
D、1728![]()
5、数列![]() 满足
满足![]() 并且
并且![]() 。则数列的第100项为( )
。则数列的第100项为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、把函数![]() 的图象向右平移1个单位,再向上平移1个单位所得图形与函数
的图象向右平移1个单位,再向上平移1个单位所得图形与函数![]() 的图象关直线
的图象关直线![]() 对称,则函数
对称,则函数![]() ( )
( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
7、有五名应聘者同时参加某单位的招聘考试,按成绩排成第一名到第五名的名次,甲、乙两名应聘者去询问考试结果,回答者对甲说:“很遗憾,你和乙都不是第一名。”对乙说:“你当然也不是最后一名”。那么这五人的名次排列一共有几种不同的情况( )
 A、72 B、60 C、54 D、48
A、72 B、60 C、54 D、48
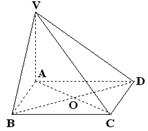
8、四棱锥![]() 的底面是边长为4的菱形,且
的底面是边长为4的菱形,且![]()
![]() ,VA=3,则异面直线BD和VC的距离为( )
,VA=3,则异面直线BD和VC的距离为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、已知函数![]() ,则
,则![]() 的值是( )
的值是( )
A、1 B、2 C、3 D、4
10、若椭圆![]() 和双曲线
和双曲线![]() 有相同的焦点
有相同的焦点![]() ,且P是两条曲线的一个交点,则
,且P是两条曲线的一个交点,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、若![]() ,则不等式
,则不等式![]() 的解集(
):
的解集(
):
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、已知函数![]() (定义域为D,值域为A)有反函数
(定义域为D,值域为A)有反函数![]() ,则方程
,则方程![]() 有解
有解![]() ,且
,且![]() 的充要条件是
的充要条件是![]() 满足( )
满足( )
A、![]() B、
B、![]()
C、![]() 的图象位于
的图象位于![]() 的下方
的下方
D、![]() 且与
且与![]() 轴的交点为(0,
轴的交点为(0,![]() )
)
二、填空题
13、已知![]() ,则
,则![]()
14、若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围
的取值范围![]()
15、在二项式![]() 和
和![]() 的展开式中,各项系数之和记为
的展开式中,各项系数之和记为![]() 是正整数,则
是正整数,则![]() =
=![]()
16、已知集合A,B,C,ABA={直线},B={平面},C=A![]() B,若
B,若![]() 在下列命题中
在下列命题中
①![]() ②
②![]() ③
③ ![]() ④
④![]()
正确命题的序号是_______________(把你认为正确的序号都填上)
三、解答题
17、在![]() 中,求:
中,求:![]() 的值.
的值.
18、解关于x的不等式:
![]()
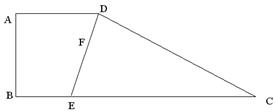
19、如图,已知直角梯形ABCD中,AB⊥BC,AB=AD=a,BC=3a,E是BC边上一动点,以DE为棱把△CDE折起,使其成为直二面角C—DE—A,求四棱锥C—ABED体积的最大值。
20、甲、乙两家电公司,2000年的市场占有率均为A,根据市场分析和预测,甲公司从2000年(第一年)起市场占有率![]() 与
与![]() 呈抛物线(如图一),乙公司自2000年起逐年的市场占有率
呈抛物线(如图一),乙公司自2000年起逐年的市场占有率![]() 都有所增加,规律如图二。
都有所增加,规律如图二。
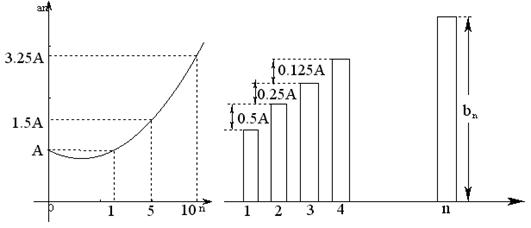
图一 图二
(1) 根据两图信息,求出两公司第![]() 年市场占有率
年市场占有率![]() ,
,![]() 的表达式。
的表达式。
(2) 根据甲、乙两公司所在地的市场规律,如果某公司市场占有率不足另一公司市场占有率的20%,则该公司将被另一公司兼并,经计算2019年之前不会出现兼并局面,试问2019年是否会出现兼并局面,并说明理由。
21、已知椭圆E的两焦点分别为![]() ,椭圆的弦AB过点
,椭圆的弦AB过点![]() ,且
,且![]() 的周长为
的周长为![]() 。
。
(1) 求椭圆E的方程。
(2) P为椭圆E上任一点,O为坐标原点,以P为直角顶点,按逆时针方向作一等腰![]() ,求Q点的轨迹方程。
,求Q点的轨迹方程。
22、设函数![]() 在R上单调,对任意
在R上单调,对任意![]() ,都有
,都有![]()
(1) 判断![]() 的奇偶性
的奇偶性
(2) 求证:若![]()
(3) 试证:若![]()
高三联考数学试卷
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题
13、______________________ 14、______________________
15、______________________ 16、______________________
三、解答题(共计74分)
17、(11分)在![]() 中,求:
中,求:![]() 的值.
的值.
18、(11分)解关于x的不等式:![]()
 19、(12分)如图,已知直角梯形ABCD中,AB⊥BC,AB=AD=a,BC=3a,E是BC边上一动点,以DE为棱把△CDE折起,使其成为直二面角C—DE—A,求四棱锥C—ABED体积的最大值。
19、(12分)如图,已知直角梯形ABCD中,AB⊥BC,AB=AD=a,BC=3a,E是BC边上一动点,以DE为棱把△CDE折起,使其成为直二面角C—DE—A,求四棱锥C—ABED体积的最大值。
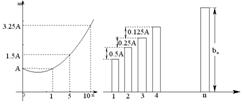 20、(14分)甲、乙两家电公司,2000年的市场占有率均为A,根据市场分析和预测,甲公司从2000年(第一年)起市场占有率
20、(14分)甲、乙两家电公司,2000年的市场占有率均为A,根据市场分析和预测,甲公司从2000年(第一年)起市场占有率![]() 与
与![]() 呈抛物线(如图一),乙公司自2000年起逐年的市场占有率
呈抛物线(如图一),乙公司自2000年起逐年的市场占有率![]() 都有所增加,规律如图二。(1)根据两图信息,求出两公司第
都有所增加,规律如图二。(1)根据两图信息,求出两公司第![]() 年市场占有率
年市场占有率![]() ,
,![]() 的表达式。(2)根据甲、乙两公司所在地的市场规律,如果某公司市场占有率不足另一公司市场占有率的20%,则该公司将被另一公司兼并,经计算2019年之前不会出现兼并局面,试问2019年是否会出现兼并局面,并说明理由。
的表达式。(2)根据甲、乙两公司所在地的市场规律,如果某公司市场占有率不足另一公司市场占有率的20%,则该公司将被另一公司兼并,经计算2019年之前不会出现兼并局面,试问2019年是否会出现兼并局面,并说明理由。
21、(12分)已知椭圆E的两焦点分别为![]() ,椭圆的弦AB过点
,椭圆的弦AB过点![]() ,且
,且![]() 的周长为
的周长为![]() 。
。
(3) 求椭圆E的方程。
(4) P为椭圆E上任一点,O为坐标原点,以P为直角顶点,按逆时针方向作一等腰![]() ,求Q点的轨迹方程。
,求Q点的轨迹方程。
22、(14分)设函数![]() 在R上单调,对任意
在R上单调,对任意![]() ,都有
,都有![]()
(4) 判断![]() 的奇偶性
的奇偶性
(5) 求证:若![]()
(6) 试证:若![]()
高三联考数学答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | C | C | D | C | C | D | C | A | B | D |
二、填空题:
![]()
![]()
![]()
![]()
![]() 13、
13、 ![]() 14、
14、 ![]() 15、
15、 ![]() 16、 ④
16、 ④ ![]()
三、解答题:
17、解:解:在![]() 中
中
![]()
![]() (3分)
(3分)
![]() (5分)
(5分)
![]() (7分)
(7分)
![]() (9分)
(9分)
![]() (11分)
(11分)
18、原不等式化简为:
![]() (1分)
(1分)
(1) 当![]() 时,不等式化为:
时,不等式化为:
![]() (4分)
(4分)
(2)
当![]() 时,不等式化为:
时,不等式化为:
![]() (7分)
(7分)
(3) 当![]() 时,不等式化为:
时,不等式化为:
![]()
与题设条件相矛盾。
综上所述:![]() (10分)
(10分)
故:当![]() 时:解集
时:解集![]()
当![]() 时:解集
时:解集![]() (11分)
(11分)
19、解:设![]() 作
作![]() 于
于![]() 于
于![]() 则
则
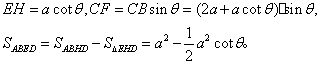
![]() 是直二面角, (4分)
是直二面角, (4分)
∴ 平面角CDE⊥平面ABED。
当E与B点重合时,![]() 有最小值:
有最小值:![]() (8分)
(8分)
当![]() 点时,
点时,![]()
当![]() 时,
时,![]() 是增函数,
是增函数,
当![]() 时,易得
时,易得![]() 是减函数,
是减函数,
∴![]() 时,V有最大值:
时,V有最大值:![]() 。 (12分)
。 (12分)
20、解:(1)由![]() (2分)
(2分)
设![]() 则
则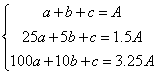 得:
得: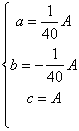
![]() (5分)
(5分)
由![]()
得 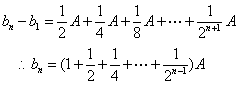
![]() (8分)
(8分)
(2)2019年,即经过20年时,
![]()
若出现兼并局面,则甲公司兼并乙公司。
此时![]()
∴到2019年,甲公司将兼并乙公司。 (14分)
21、解:(1)周长![]()
∴椭圆E的方程为:![]() (3分)
(3分)
(2)视坐标平面为复平面,设向量![]() 对应复数为
对应复数为![]()
则P(![]() ),且
),且![]() ① (5分)
① (5分)
设向量![]() 对应复数为
对应复数为![]()
则Q(![]() ),且
),且
![]()
![]() (8分)
(8分)
∴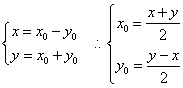 代入①
代入①
得:![]() 即为所求。 (12分)
即为所求。 (12分)
22、(1)解:令![]()
令![]() 代入得
代入得
![]()
![]() 是奇函数 (5分)
是奇函数 (5分)
(2)证明:![]()
∴对![]() 必有
必有
![]() ①
①
取![]() ,得
,得![]() ②
②
![]() 时,
时,![]()
![]() (10分)
(10分)
(3)证明:当![]() 时,由(2)可得
时,由(2)可得 ![]()
② 当![]() 时,设
时,设![]() ,由(2)中①②式得
,由(2)中①②式得
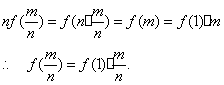
③ 当![]() 时,显然成立。
时,显然成立。
④ 当![]() 时,
时,![]() ,
,
![]()
从而对一切![]() 都有
都有![]() (14分)
(14分)