高三年级第一次教学质量检测数学试题卷4
（文理合卷）
考生须知:
1. 本卷满分150分, 考试时间120分钟.
2. 答题前, 在答题卷密封区内填写学校、班级和姓名.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
参考公式
如果事件
互斥，那么
;
如果事件相互独立，那么
;
如果事件
在一次试验中发生的概率是P，那么
次独立重复试验中恰好发生
次的概率
.
一. 选择题 : 本大题共12小题, 每小题5分, 共60分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 .
1.
在数列
中，
, 则此数列前4项之和为
(A) 0 (B) 1 (C) 2 (D) -2
2. 函数
的值域是
(A) 
(B) 
(C) 
(D) 
3. (理科)
随机变量
的等可能取值为1，2，3，…
, , 如果
，那么n的值为
(A) 3 (B) 4 (C) 10 (D)12
（文科）对总数为
的一批零件抽取一个容量为30的样本，若每个零件被抽取的概率为
，则的值为
(A) 120 (B) 200 (C) 150 (D) 100
4.
若函数
的图象和
的图象关于点
对称，则
的表达式是
(A) 
(B) 
(C) 
(D) 
5. 设
的展开式中，二项式系数的和为256，则此二项展开式中系数最小的项是
(A) 第5项 (B) 第4, 5两项 (C) 第5, 6两项 (D) 第4, 6两项
6. 已知i, j为互相垂直的单位向量，a = i – 2j, b = i + λj，且a与b的夹角为锐角，则实数
的取值范围是
(A) 
(B) 
(C) 
(D)
7. 已知
，全集U= R，集合
={
＜
＜
={
＜＜
，
={＜≤
，则
满足的关系是
(A) P =M∪N. (B) P=M∪N .
(C) P=M∩(Ú UN ). (D) P = (Ú UM)∩N.
|
|
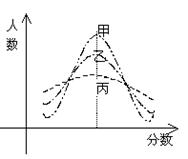
8. （理科）某次市教学质量检测，甲、乙、丙三科考试
成绩的直方图，如右图所示 (由于人数众多，成绩分
布的直方图可视正态分布)，则由如图曲线可得下列说
法中正确的一个是
(A) 甲科总体的标准差最小
(B) 丙科总体的平均数最小
(C) 乙科总体的标准差及平均数都居中 (D) 甲、乙、丙的总体的平均数不相同
（文科）从湖中打一网鱼, 共条, 做上记号再放回湖中,
数天后再打一网鱼共有条, 其中有条有记号, 则能估计湖中有鱼 ( )
(A) 
(B)
(C)
(D) 
9. (理科) 设△
的两个内角
所对的边分别为
，复数
,
, 若复数
在复平面上对应的点在虚轴上，则△是
(A) 等腰三角形或直角三角形 (B) 等腰直角三角形
(C) 等腰三角形 (D) 直角三角形.
（文科）函数
, 如果方程
有且只有一个实根，那么实数应满足
(A) 
(B) 
(C) 
(D) 
10. 设
为坐标平面内一点，
为坐标原点，
记
，当变化时，函数的最小正周期是
(A) 
(B)
(C)30 (D)
15
11. (理科) 点
在曲线
上移动，设点处切线的倾斜角为
，则a的取值范围是
(A) 
(B)
(C) 
(D) 
(文科)
若函数f ( x ) = x3 + ax2
+ bx – 7在
上单调递增, 则实数a,
b一定满足的条件是
(A) 
(B) 
(C) 
(D) 
12. 已知函数图象
与
关于直线
对称, 且图象关于点 (2 ,–3)对称, 则的值为
(A) 3 (B) –2 (C) 2 (D) –3
二. 填空题: 本大题有4小题, 每小题4分, 共16分. 请将答案填写在题中的横线上.
13. (理科) 
的值为________ .
(文科) “面积相等的三角形全等”的否命题是 ______ 命题 . (填 “真” 或者 “假”)
14. 已知
且
, 
为锐角, 则
的值为 _______________ .
15. 某乡镇现有人口1万, 经长期贯彻国家计划生育政策,目前每年出生人数与死亡人数分别为年初人口的0.8% 和1.2%， 则经过2年后，该镇人口数应为 __________________ (结果精确到0.01).
16. “渐升数”是指每个数字比其左边的数字大的正整数（如34689）. 则五位“渐升数”共有 个，若把这些数按从小到大的顺序排列，则第100个数为_______ .
三. 解答题 :本大题有6小题, 共74分. 解答应写出文字说明, 证明过程或演算步骤.
17. (本小题满分12分)
设△的内角
成等差数列，且满足条件
,
试判断△的形状，并证明你的结论.
18. (本小题满分12分)
从汽车东站驾车至汽车西站的途中要经过8个交通岗，假设某辆汽车在各交通岗遇到红灯的事件是独立的，并且概率都是
.
（1）求这辆汽车首次遇到红灯前，已经过了两个交通岗的概率;
（2）（理）这辆汽车在途中遇到红灯数ξ的期望与方差．
（文）这辆汽车在途中恰好遇到4次红灯的概率．
19. (本小题满分12分)
已知平面向量 a与b 不共线，若存在非零实数
, 使得 c = a +2b ,
d =–
a + 
b .
(1) 当c= d时，求
的值;
(2) 若a = (cos
, sin(–)), b = (sin, cos)，且c⊥d , 试求函数的表达式.
20. (本小题满分12分)
已知一物体做圆周运动, 出发后
分钟内走过的路程
, 最初用5分钟走完第一圈, 接下去用3分钟走完第二圈.
(1) 试问该物体走完第三圈用了多长时间? (结果可用无理数表示)
(2) (理科做文科不做) 试问从第几圈开始, 走完一圈的时间不超过1分钟?
21. (本小题满分12分)
已知数列，其中
, 数列
的前项的和
.
(1) 求数列的通项公式;
(2) 求数列的通项公式;
(3) (理科做文科不做) 求数列
的前n项和
.
22. (本小题满分14分)
定义在定义域D内的函数
，若对任意的
都有
，则称函数为“西湖函数”，否则称“非西湖函数”.函数
是否为“西湖函数”?如果是，请给出证明；如果不是，请说明理由.
|
|
23. (附加题, 本题满分6分, 但全卷总分不超过150分)
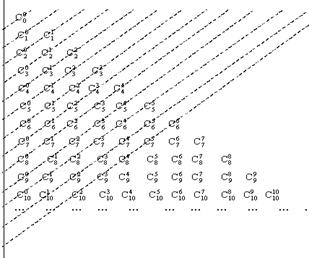
把“杨辉三角形”向左对齐如图所示，
分别按图中虚线，由上至下把划到的数相加，
写在虚线左下端点（左边竖线的左侧）处，
把这些和由上至下排列得一个数列.
(1) 观察数列，写出一个你能发
现的递推公式（不必证明）；
(2) 设
,
求
的值, 并求
.
高考科目教学质量第一次检测
数学参考评分标准 (文理合卷)
一. 选择题 : 本大题共12小题. 每小题5分, 共60分. (理/文)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | A | D | C/A | B | D | B | C | A/A | A/C | D | B/A | C |
二. 填空题 : 本大题共4小题. 每小题4分, 共16分.
13. 
/真 14. 
15. 0.99 16.
126, 24789
三. 解答题: 本大题共6小题, 共74分.
17. (本小题满分12分)
∵ 
，∴ 
.
由 , 得
即 
又 
, ∴ 
, △为等边三角形.
18. (本小题满分12分)
（1）∵ 这辆汽车在第一、二个交通岗均未遇到红灯，而第三个交通岗遇到红灯
∴ 概率 = (1 –
)(1 –) = 
;
（2）（理）∵
∽
( 8, ),
∴ 期望
8´=
, 方差
= 8´´( 1 –) = 
.
（文）概率 = 
´()4´ (1–)2 = 
. 
19. (本小题满分12分)
(1) 由条件得：a +2b
=–a + b,
∴ 
a +
b = 0 ,
∵向量 a与b 不共线, ∴ 
,
解得 
或 
.
(2) ∵ a·b = cossin+ sin(–)cos = 0, ∴a⊥b .
又∵c⊥d , ∴c·d = 0.
∵由条件知: a = 1, b = 1, a·b = 0,
∴ c·d = (a +2b)·[–a + b]
a 2 
a·b+a·b
)b 2 
.
∴ 
, 即
.
20. (本小题满分12分)
(1) 设圆周长为
, 依题意有 
, 可表示为 
.
设出发分钟后走完第三圈, 则
, 上式代入, 得
, ∵ 
, ∴ 解得
,
所以走完第三圈需用时间为
(分钟).
(2) 设出发分钟后走完第圈, 则
,
解得 
(分钟), 则走完
圈需
(分钟),
依题意应有 
, 解此不等式, 得
,
所以, 从第16圈开始, 走一圈所用时间不超过1分钟.
21. (本小题满分12分)
（1）
, 累加得
,
∴ 
, 则
.
或者用累乘得 a n = 
=
.
（2）∵ , ∴ 
;
而
, 当
时, 
, 
时也适合,
所以数列
的通项公式为 
.
(3) 当
, 即
时, 
,
当
，即n >3时，
,
综上所述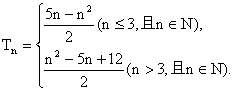 
.
22. (本小题满分14分)
因为
,
函数的导数是
,
当
时，即
,
当
时，
；当
时，
，
故
在
内的极小值是a - 
;
同理, 在内的极大值是a+ ;
因为
，所以函数的最大值是a + ，最小值是a - , 故 
,
所以函数是“西湖函数”.
23. 附加题: (本小题满分5分, 但全卷不超过150分)
(1)a1 = a2 = 1, an+2 = a n +1 + an
(2) A=
, B=
或A=, B=
an = 
[()n –()n]