高三补习班数学单元检测题——数列
一、选择题(每小题5分,共60分)
1.数列![]() 的一个通项公式是
(
)
的一个通项公式是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.数列![]() 中,
中,![]() ,对所有的n≥2,都有
,对所有的n≥2,都有![]() ,则
,则![]() 等于(
)
等于(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设![]() ,则( )
,则( )
A.S(n)共有n项,当n=2时,![]() 。
。
B.S(n)共有n+1项,当n=2时,![]() 。
。
C.S(n)共有![]() 项,当n=2时,
项,当n=2时,![]() 。
。
D.S(n)共有![]() 项,当n=2时,
项,当n=2时,![]() 。
。
4.在数列![]() ,
,![]() ,…,
,…,![]() ,…的每相邻两项中间插入3个数,使它们与原数列构成一个新数列,则新数列的第29项( )
,…的每相邻两项中间插入3个数,使它们与原数列构成一个新数列,则新数列的第29项( )
A.不是原数列的项 B.是原数列的第7项C.是原数列的第8项D.是原数列的第9项
5.在等差数列![]() 中,
中,![]() ,
,![]() ,
,![]() 是其前n项和,则( )
是其前n项和,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知a、1、c成等差数列,![]() 、1、
、1、![]() 成等比数列,则
成等比数列,则![]() 等于( )
等于( )
A.1 B.3
C.1或![]() D.3或
D.3或![]()
7.已知等比数列![]() 的公比q<0,其前n项和为
的公比q<0,其前n项和为![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
8.一直角三角形三边边长成等比数列,则( )
A.三边边长之比为3:4:5 B.三边边长之比为![]()
C.较小锐角的正弦值![]() D.较大锐角的正弦值
D.较大锐角的正弦值![]()
9.![]() 是一个等差数列且
是一个等差数列且![]() ,
,![]() .若
.若![]() ,则
,则
k等于 ( )
A.16 B.18 C.20 D.22
10.已知数列![]() 的首项
的首项![]() ,又满足
,又满足![]() 则该数列的通项
则该数列的通项![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.三个数6,3,-1顺次排成一行,在6和3之间插入两个实数,在3和-1之间插入一个实数,使得这六个数中的前三个、后三个组成等差数列,且插入的三个数本身顺次成等比数列,那么所插入的三个数的和是 ( )
A.7
B.![]() C.
C.![]() D.7或
D.7或![]()
12.数列1,2,2,3,3,3,4,4,4,4,……中,第100项是( )
A.10 B.13 C.14 D.100
二、填空题(每小题4分,共16分)
13.若lgx,lg(3x-2),lg(3x+2)成等差数列,则![]() 的值是________。
的值是________。
14.已知数列![]() 的首项为5,且
的首项为5,且![]() ,则
,则![]() .
.
15.等差数列![]() 的前n项和为Sn,且
的前n项和为Sn,且![]() 如果存在正整数M,使得对一切正整数n,
如果存在正整数M,使得对一切正整数n,![]() 都成立.则M的最小值是
.
都成立.则M的最小值是
.
16.观察前4个等式: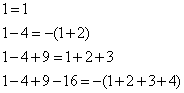 ,猜测第n个等式为______________.
,猜测第n个等式为______________.
三、解答题(共74分)
17.(本小题满分12分)已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,令
,令![]() ,且
,且![]() 求数列
求数列![]() 的通项公式。
的通项公式。
18.(本小题满分12分)已知数列![]() 满足
满足![]() ,且数列
,且数列![]() 的前n项和
的前n项和![]() 满足
满足![]() ,
,![]() ,数列
,数列![]() 的前n项和
的前n项和![]() 满足
满足![]()
(1)
求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)
令![]() ,问是否存在正整数m,使得对任意n都有
,问是否存在正整数m,使得对任意n都有![]() ,若存在求之;若不存在,说明理由。
,若存在求之;若不存在,说明理由。![]()
19.(本小题满分12分)设各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,对于任意的正整数n都有等式
,对于任意的正整数n都有等式![]() 成立.
成立.
(Ⅰ)求![]() ;
;
(Ⅱ)求证![]() ;
;
(III)(文科)求![]() .
.
20.(本小题满分12分)为促进个人住房商品化的进程,我国1999年元月公布了个人住房公积金贷款利率和商业性贷款利率如下:
| 贷款期(年数) | 公积金贷款月利率(‰) | 商业性贷款月利率(‰) |
| …… 11 12 13 14 15 …… | …… 4.365 4.455 4.545 4.635 4.725 …… | …… 5.025 5.025 5.025 5.025 5.025 …… |
夏先生家要购买一套商品房,计划贷款25万元,其中公积金贷款10万元,分十二年还清;商业贷款15万元,分十五年还清.每种贷款分别按月等额还款,问:
(I) 汪先生家每月应还款多少元?
(II) 在第十二年底汪先生家还清了公积金贷款,如果他想把余下的商业贷款也一次性还清;那么他家在这个月的还款总数是多少?
(参考数据:1.004455144=1.8966,1.005025144=2.0581,1.005025180=2.4651)
21.(本小题满分12分)在直角坐标平面上有一点列
![]() 对每个正整数n,点Pn位于函数
对每个正整数n,点Pn位于函数![]() 的图
的图
象上,且Pn的横坐标构成以![]() 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,第n条抛物线Cn的顶点为Pn且过点Dn(0,n2+1),记过点Dn且与抛物线Cn只有一个交点的直线的斜率为kn,求![]()
(3)设S=![]() 等差数列{an}的任一项
等差数列{an}的任一项
an∈S∩T,其中a1是S∩T中的最大数,―265<a10<―125,求{an}的通项公式.
22.(本小题满分14分)已知数列{![]() }满足条件:
}满足条件:![]() ,
,![]() (r>0),{
(r>0),{![]() }是公比q(q>0)的等比数列,设
}是公比q(q>0)的等比数列,设![]() (n
(n![]() N).
N).
(1)求出使不等式![]() (n
(n![]() N)成立的q的取值范围;
N)成立的q的取值范围;
(2)设![]() ,
,![]() ,求数列{
,求数列{![]() }的最大项和最小项的值;
}的最大项和最小项的值;
(3)(理科)设![]() ,求
,求![]() 和
和![]() .
.
高三补习班数学单元检测题——数列
CADCB CAACBB BC
13 ![]() 14
15.2;.
14
15.2;.
16 ![]()
17、![]() , ,
, , ![]() 。
。
18.![]()
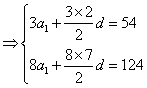
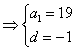
![]() ………..3
………..3
![]()
![]()
![]()
![]() …………………….6
…………………….6
(2) ![]()
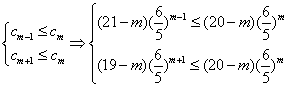
![]() ………………………………………………………….12
………………………………………………………….12
19. Ⅰ.当n=1时,![]() .
Ⅱ.当
.
Ⅱ.当![]() 时,
时,![]()
![]()
当n=1时,也符合![]()
![]()
Ⅲ. 当![]() 时,
时,![]()
![]()
![]() ,
, ![]()
于是数列![]() 是首项为2,公差为2的等差数列.
是首项为2,公差为2的等差数列.
![]() ,
, ![]() ,
, ![]()
![]() .
.
20.设月利率为r,每月还款数为a元,总贷款数为A元,还款期限为n月.
第1月末欠款数 A(1+r)-a,
第2月末欠款数 [A(1+r)-a](1+r)-a= A(1+r)2-a (1+r)-a,
第3月末欠款数 [A(1+r)2-a (1+r)-a](1+r)-a =A(1+r)3-a (1+r)2-a(1+r)-a,
……
第n月末欠款数 ![]() ,
,
得:![]() .
.
(I) 对于12年期的10万元贷款,n=144,r=4.455‰,
∴![]() ,
,
对于15年期的15万元贷款,n=180,r=5.025‰,
∴![]() .由此可知,汪先生家前12年每月还款942.37+1268.22=2210.59元,后3年每月还款1268.22元.
.由此可知,汪先生家前12年每月还款942.37+1268.22=2210.59元,后3年每月还款1268.22元.
(II) 至12年末,汪先生家按计划还款以后还欠商业贷款
![]() .
.
其中A=150000,a=1268.22,r=5.025‰ , ∴X=41669.53.
再加上当月的计划还款数2210.59元,当月共还款43880.12元.
21.(I)![]()
![]() ∴点Pn坐标为
∴点Pn坐标为![]()
(II)设Cn方程为:![]() ,①
,①
把Dn(0,n2+1)代入①式得:a=1,∴Cn方程为:![]()
过点Dn且斜率为kn的直线ln 的方程为:![]()
把ln代入Cn得![]() ,∴ln与Cn只有一个交点 ∴△=0,即kn=2n+3.
,∴ln与Cn只有一个交点 ∴△=0,即kn=2n+3.
![]()
(III)![]()
T=![]()
∴![]() . T中最大数为a1=-17,设{an}的公差为d,则
. T中最大数为a1=-17,设{an}的公差为d,则
![]() 由此得:
由此得:![]()
又![]()
![]()
22.(1)设{![]() ,
,![]() }的公比为q(
}的公比为q(![]() )且
)且![]() ,
,![]() (
(![]() ),由不等式
),由不等式![]()
![]() (2)∵
(2)∵ ![]() (
(![]() N),
N),![]() .又
.又![]() ,∴
,∴ ![]() .又
.又![]()
![]() =(1+r)
=(1+r)![]() ,
,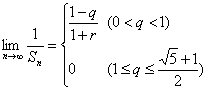
(3)![]() .∴
.∴ ![]() .设
.设![]() ,则①当
,则①当![]() 时,
时,![]() .∴ 当
.∴ 当![]() 时,
时,![]() 最小(
最小(![]() ),
),![]() ;②当
;②当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 最大(
最大(![]() ).
).![]()
21.(本小题满分12分)已知函数![]() ,数列
,数列![]() 满足
满足![]()
![]() 且
且![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 的通项
的通项![]() ,
,![]() 的前
的前![]() 项之和为
项之和为![]() ,试比较
,试比较![]() 和
和![]() 的大小. 21.(12分)(1)解:由
的大小. 21.(12分)(1)解:由![]() ,得
,得![]() ,
,
又![]()
![]()
![]() ,
,
所以![]() 是首项
是首项![]() ,公差为1的等差数列,故
,公差为1的等差数列,故![]() 即
即![]() 。
。
(2)由(1)得![]() ,所以
,所以![]()
![]() ,令
,令![]()
解得:![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]() 。
。