高三补习班数学单元检测题——
 圆锥曲线
圆锥曲线
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分).
1.已知log2a,log2b,2成等差数列,则M(a,b)的轨迹为 ( )
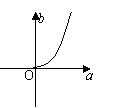
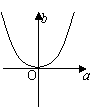
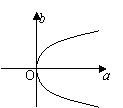
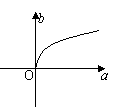
(A) (B) (C) (D)
2、抛物线![]() 的焦点坐标是 ( )
的焦点坐标是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.双曲线kx2+5y2=5的一个焦点是(0,2),则k等于( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
4.设θ是三角形的一个内角,且![]() ,则方程
,则方程![]() 表示( )
表示( )
(A) 焦点在x轴上的椭圆 (B) 焦点在y轴上的椭圆
(C) 焦点在x轴上的双曲线 (D) 焦点在y轴上的双曲线
5.已知椭圆![]() 和抛物线
和抛物线![]() 的离
的离
心率分别为e1、e2、e3,则 ( )
A.e1e2> e3 B.e1e2= e3 C.e1e2< e3 D.e1e2≥e3
6.设F1、F2为椭圆![]() +y2=1的两个焦点,P在椭圆上,当△F1PF2面积为1时,
+y2=1的两个焦点,P在椭圆上,当△F1PF2面积为1时,![]() ·
·![]() 的值为( )
的值为( )
A.0 B.1 C.2 D.![]()
7.椭圆![]() 的焦点为F1和F2,点P在椭圆上,若线段PF1的中点在y轴上,则
的焦点为F1和F2,点P在椭圆上,若线段PF1的中点在y轴上,则
![]() 的值为 ( )
的值为 ( )
A.5:1 B.7:1 C.9:2 D.8:3
8、已知双曲线的中心在原点,两个焦点![]() 坐标分别为
坐标分别为![]() 和
和![]() ,P在双曲线上,满足
,P在双曲线上,满足![]() 且
且![]() 的面积为1,则此双曲线的方程是( )
的面积为1,则此双曲线的方程是( )
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]()
9、现有一块长轴长为10分米,短轴长为8分米的椭圆形玻璃镜子,欲从此镜中划出一块面积尽可能大的矩形镜子,则可划出的矩形镜子的最大面积为 ( )
A、10平方分米 B、20平方分米 C、40平方分米 D、![]() 平方分米
平方分米
10.设椭圆![]() 和双曲线
和双曲线![]() 的公共焦点为F1、F2,P 是两曲线是一个公共点,则
的公共焦点为F1、F2,P 是两曲线是一个公共点,则![]() 的值等于
( )
的值等于
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()

|
|


物线于点A、B,交其准线于点C,若![]() ,且
,且![]() ,
,
|
|
|
|
|
|
12.椭圆 ![]() =1(a>b>0)的半焦距为C,若直线y=2x与椭圆一个交点的横坐标恰为C,则椭圆离心率为( )
=1(a>b>0)的半焦距为C,若直线y=2x与椭圆一个交点的横坐标恰为C,则椭圆离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
13、以双曲线两焦点为直径端点的圆与双曲线的四个交点连同双曲线的焦点恰好构成一个正六边形,则该双曲线的离心率为
14.设![]() 、
、![]() ,常数
,常数![]() ,定义运算
,定义运算![]() ,若
,若![]() ,则动点
,则动点![]() 的轨迹方程是__________________.
的轨迹方程是__________________.
15.椭圆![]() 上到两个焦点距离之积最小的点的坐标是
.
上到两个焦点距离之积最小的点的坐标是
.
16.已知F为抛物线y2=2ax的焦点,P为此抛物线上任一点,O为坐标原点,以下四个命题:
①△FOP为等边三角形 ②△FOP为等腰直角三角形
③△FOP为直角三角形 ④△FOP为等腰三角形
其中一定不正确的命题的序号是 .
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)曲线C:![]()
(Ⅰ)若曲线C是椭圆,求k的取值范围;
(Ⅱ)若曲线C是双曲线,且有一条渐近线的倾斜角是60°,求此双曲线的方程;
(Ⅲ)满足(Ⅱ)的双曲线上是否存在两点P,Q关于直线l:y=x-1对称,若存在,求出过P,Q的直线方程;若不存在,说明理由.
18.(本小题满分12分)蔬菜地的灌溉,不少农户使用旋转式自动喷水器,已知一喷水器高1.5米,喷出的水雾成抛物线状,喷头与水流最高点的连线与水平面成30°角,水流的最高点比喷头高出1.5米,用这种喷水器一次能灌溉多大面积?(精确到十分位)
19. (本小题满分12分)椭圆![]() ,P点(0,3),过P引直线L和椭圆交于A、B,且A点位于B和P之间。
,P点(0,3),过P引直线L和椭圆交于A、B,且A点位于B和P之间。
(1)求![]() 的范围。
的范围。
(2)是否存在直线L,使以AB为直径的圆过原点0。(14分)
20.(本小题满分12分)一条斜率为1的直线l与离心率为![]() 的双曲线
的双曲线![]() =1(a>0,b>0)交于P、Q两点,直线l与y轴交于R点,且
=1(a>0,b>0)交于P、Q两点,直线l与y轴交于R点,且![]() ·
·![]() =-3,
=-3,![]() =3
=3![]() ,求直线与双曲线的方程.
,求直线与双曲线的方程.

 21.(本小题满分12分) 已知椭圆
21.(本小题满分12分) 已知椭圆![]() 的一条准线方程是
的一条准线方程是![]() 其左、右顶点分别是A、B;双曲线
其左、右顶点分别是A、B;双曲线![]() 的一条渐近线方程为3x-5y=0.
的一条渐近线方程为3x-5y=0.
(Ⅰ)求椭圆C1的方程及双曲线C2的离心率;
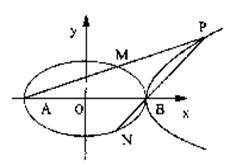
(Ⅱ)在第一象限内取双曲线C2上一点P,连结AP交椭圆C1于点M,
|
|
22.(本小题满分14分)已知双曲线![]() =1(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
=1(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若PF=3,且双曲线的离心率e=![]() ,求该双曲线方程;
,求该双曲线方程;
(3)延长FP交双曲线左准线l1和左支分别为点M、N,若M为PN的中点,求双曲线的离心率.
单元检测题——圆锥曲线参考答案
1—5 : AABBC 6---10 : ABACB 11---12 BB
13、√3+1 ;14、y=x+a ;15.(±5,0); 16.①②
17.(I)当k=0或k=-1或k=4时,C表示直线;
当k≠0且k≠-1且k≠4时方程为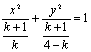 方程(1)表示椭圆的充要条件是
方程(1)表示椭圆的充要条件是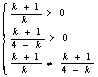 即是0<k<2或2<k<4
即是0<k<2或2<k<4
(Ⅱ)方程(1)表示双曲线的充要条件是![]() 即k<-1或-1<k<0或k>4(i)当k<-1或k>4时,双曲线焦点在x轴上,
即k<-1或-1<k<0或k>4(i)当k<-1或k>4时,双曲线焦点在x轴上,![]() ,
,![]() ,
,
其一条渐近线的斜率为![]() 得k=6
得k=6
(ii)当-1<k<0时,双曲线焦点在y轴上,![]() ,
,![]() ,其一条渐近线的斜率为
,其一条渐近线的斜率为![]() ,得k=6(舍)综上得双曲线方程为
,得k=6(舍)综上得双曲线方程为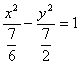
(Ⅲ)若存在,设直线PQ的方程为:y=-x+m
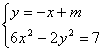 消去y,得
消去y,得![]() (2
(2
设P,Q的中点是![]() ,则
,则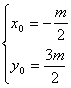 ,M的直线l上,∴
,M的直线l上,∴![]() ,
,
解得![]() ,方程(2)的△>0,∴存在满足条件的P、Q,直线PQ的方程为
,方程(2)的△>0,∴存在满足条件的P、Q,直线PQ的方程为![]()
18.解:先如图建系,喷头为![]() ,水流最高点为
,水流最高点为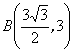 ,
,
设方程: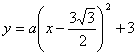 将
将![]() 代入得a=
代入得a=![]() ,
,
∴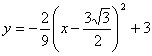 令y=0,即
令y=0,即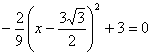
解得![]() 即
即![]()
∴![]() 19.①若k不存在,则
19.①若k不存在,则![]() --1’
--1’
②若k存在,设L方程为y=kx+3 A(x1,y1),B(x2,y2)
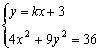 ∴(4+9k2)x2+54kx+45=0---------3’
∴(4+9k2)x2+54kx+45=0---------3’
△=54k2-4(9k2+4)·45>0--4’∴![]() -5’
-5’
![]() -------6’
-------6’
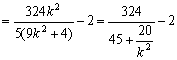 ∴2<μ<
∴2<μ< ![]() --7’
--7’
令t=![]() (0<t<1)
2<
(0<t<1)
2<![]() <
<![]() ∴
∴ ![]() <t<1
<t<1
∴-1<![]() <-
<- ![]() 综合①②,-1<
综合①②,-1<![]() ≤-
≤-![]() ---------8’
---------8’
(2)∵0在圆上,AB为直径 ∴OA⊥OB,x1x2+y1y2=0
∵x1x2+(k x1+3)(kx2+3)=0
∴(1+k2)x1x2+3k(x1+x2)+9=0-..12’
∴(1+k2)![]() +3k·
+3k·![]() +9=0 k2=
+9=0 k2=![]() ,符合k2>
,符合k2>![]()
 ∴存在这样的直线..14’
∴存在这样的直线..14’
20.∵e=![]() ,∴b=2a2,∴双曲线方程可化为2x2-y2=2a2, 2分
,∴b=2a2,∴双曲线方程可化为2x2-y2=2a2, 2分
设直线方程为y=x+m,
由![]() 得x2-2mx-m2-2a2=0. 4分
得x2-2mx-m2-2a2=0. 4分
∵Δ=4m2+4(m2+2a2)>0,∴直线一定与双曲线相交, 6分
设P(x1,y1),Q(x2,y2),则x1+x2=2m,x1x2=-m2-2a2,∵![]() =3
=3![]() ,
,
∴xR=![]() ,x1=-3x2,∴x2=-m,-3x22=-m2-2a2,消去x2得,m2=a2, 8分
,x1=-3x2,∴x2=-m,-3x22=-m2-2a2,消去x2得,m2=a2, 8分
![]() ·
·![]() =x1x2+y1y2=x1x2+(x1+m)(x2+m)=2x1x2+m(x1+x2)+m2=m2-4a2=-3, 10分
=x1x2+y1y2=x1x2+(x1+m)(x2+m)=2x1x2+m(x1+x2)+m2=m2-4a2=-3, 10分
∴m=±1,a2=1,b2=2,直线方程为y=x±1,
双曲线方程为x2-![]() =1. 12分21.(I)由已知
=1. 12分21.(I)由已知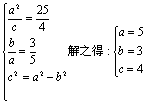 …3分∴椭圆的方程为
…3分∴椭圆的方程为![]() ,双曲线的方程
,双曲线的方程![]() .
.
又![]() ∴双曲线的离心率
∴双曲线的离心率![]() …………………………6分
…………………………6分
(Ⅱ)由(Ⅰ)A(-5,0),B(5,0) 设M![]() 得m为AP的中点
得m为AP的中点
∴P点坐标为![]() 将m、p坐标代入c1、c2方程得
将m、p坐标代入c1、c2方程得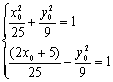
消去y0得![]() 解之得
解之得![]() 由此可得P(10,
由此可得P(10,![]() ………9分
………9分
当P为(10,![]() 时 PB:
时 PB:![]() 即
即![]()
代入![]()
![]() MN⊥x轴 即
MN⊥x轴 即![]() …………12分
…………12分
22.(1)右准线为x=![]() ,由对称性不妨设渐近线l为y=
,由对称性不妨设渐近线l为y=![]() x,
x,
则P(![]() ),又F(c,0),∴
),又F(c,0),∴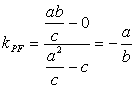 , 2分
, 2分
又∵![]() ,∴kPF·kl=-
,∴kPF·kl=-![]() =-1,∴PF⊥l. 4分
=-1,∴PF⊥l. 4分
(2)∵PF的长即F(c,0)到l:bx-ay=0的距离,
∴![]() =3,即b=3, 6分又
=3,即b=3, 6分又![]() ,∴
,∴![]() ,∴a=4,
,∴a=4,
故双曲线方程为![]() =1. 8分(3)PF的方程为:y=-
=1. 8分(3)PF的方程为:y=-![]() (x-c),
(x-c),
由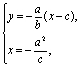 得
得![]() , 9分
, 9分
∵M是PN的中点∴![]() , 10分
, 10分
∵N在双曲线上,∴![]() ,即
,即![]() ,
,
令t=e2,则t2-10t+25=0,∴t=5,即e=![]() . 12分
. 12分