高三补习班数学单元练习（三角函数）
一、选择题：（每小题5分，共60分）
1．设集合
则M、N之间的关
系是
|
|
N B．M
N C．M=N D．
2．已知角α的终边上一点的坐标为
,则角
的最小正值为 A．
B．
C．
D．
3．函数
是 C
A．最小正周期为2π的偶函数 B．最小正周期为2π的奇函数
C．最小正周期为π的偶函数 D．最小正周期为π的奇函数
4．
的值为
A．
B．
C．
D．
5．与正弦函数
关于直线
对称的曲线是 A．
B．
C．
D．
6．设函数
那么使
恒成立的最小的正数c 等于( )
（A）
（B）
（C）
（D）1
7．已知函数
（
）的图象与直线
围成一个封闭的平面图形，那么此封闭图形的面积是
（A）4 （B）8 （C）
（D）
8．若函数
（ ）
A．3或0 B.-3或0 C.0 D.-3或3
9.设函数f(x)=2sin(
x+
)，若对任意x∈R都为f(x1)≤f(x)≤f(x2)成立，则
x1－x2的最小值是
A、4
B、2
C、1
D、
10．定义在R上的偶函数
，满足
上是减函数，又α、
β是锐角三角形的两个内角，则 A．
B．
C．
D．
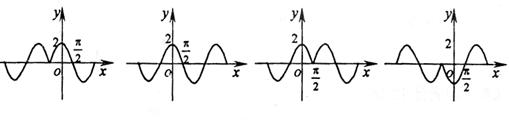
11．函数
的部分图象是 （ ）
|
A B C D
12．函数
的递减区间是 A．
B． 
C．
D．
二、填空题（每小题4分，共16分）
13．如果
.
14．设
给出
值的四个答案:
①
；②
；③
；④
.其中正确的是
.
15．给出下列五个命题，其中正确命题的序号为
①函数
的最小正周期是.
②函数
在区间
上单调递增.
③直线
是函数
的图象的一条对称轴.
④函数
的最小值是4.
⑤函数
的一个对称中心为点(π,0).
16．对于函数
，给出下列四个命题：
①存在
；
②存在
恒成立；
③存在
，使函数
的图像关于y轴对称；
④函数的图象关于点
对称；
其中正确命题的序号是
三、解答题（计74分）
17．（本小题满分12分）已知
的值.
18．（本题满分12分）
在三角形ABC中，a,b,c分别是三个内角A，B，C所对的边．
（1）若三角形ABC的面积是
，c=2,A=
。求a,b的值；
（2）若
，试判断三角形ABC的形状，并证明你的结论。
19．（本题12分）平面直角坐标系有点P(1,cosx)，Q(cosx,1)，x∈[- ,]
（Ⅰ）求向量
和
的夹角θ的余弦用x表示的函数f(x)；
（Ⅱ）求θ的最值.
20．(12分)已知函数f(x)=sin(2x+
)+sin(2x－)+cos2x+a(a为实常数)
（1） 求函数f(x)的最小正周期
（2） 求函数f(x)的单调递减区间
（3）若x∈[0，]时，f(x)的最小值为－2，求a的值。
21．（本题满分12分）是否存在锐角α、β使得（1）
；（2）
同时成立？若存在，求出α和β的值；若不存在，说明理由.
22．（本小题满分14分）设函数
的图象经过两点（0，1），（
），
且在
，求实数a的的取值范围.
高三新课程数学测试题参考答案及评分意见
CDCBA CCDCC CD
13． 
；14．①④15．③⑤16．①③④
17．
……5分
由
两边平方得
…9分
而
，故原式
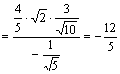……12分
18．1）由
……………………………………3分
由余弦定理得
……………………………………3分
2）由正弦定理得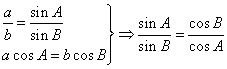
……………3分
或
或
……………………………………3分
19 1)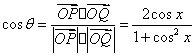 
……………………………4分
2) 
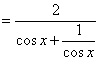
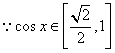易证
在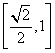
上是单调递减函数。………………4分
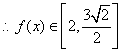
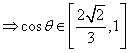……………………………4分
20.1)
……………………………4分
2)由
………………4分
3) 
…………………………4分
21．由
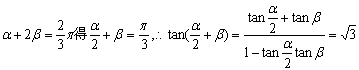……4分，
是一元二次方程
的两根，解
得
……8分. 若
矛盾，不合；
，故存在
满足条件……12分
22．由图象过两点得1=a+b，1=a+c，
……3分
………6分 当a＜1时，
，只须
解得
……9分
当
要使
解得
，故所求a
的范围是
………………13分