高三春考数学模拟试题
(满分:150分 考试时间:120分钟)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一项符合题目要求。
1.已知全集I,M、N是I的子集,若I=M∪N,M∩N≠Φ,则下列关系中不正确的是
( )
|
2.原命题“在空间没有公共点的两条直线是异面直线”则下列说法正确的是 ( )
A.原命题是真命题 B.逆命题是假命题
C.否命题是真命题 D.逆命题是真命题
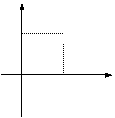
3.某学生离家去学校,一开始跑步前进,跑累了再走余下的路程。下列图中纵轴表示离校
的距离,横轴表示出发后的时间,则较符合学生走法的是 ( )
 |  |  |  |
y y y y
o x o x o x o x
A B C D
4.将曲线f(x,y)=0按向量![]() =(h,k)平移后得到曲线的方程是 ( )
=(h,k)平移后得到曲线的方程是 ( )
A.f(x-h, y+k) B.f(x-h ,y-k)=0
C.f(x+h ,y+k)=0 D.f(x+h, y-k)=0
5.在三角形ABC中“cosA+sinA=cosB+sinB”是“c=90°”的 ( )
A.充分非必要条件 B.必要非充分条件C.充要条件 D.非充分非必要条件
6.双曲线![]() 的离心率
的离心率![]() ,则k的取值范围是 ( )
,则k的取值范围是 ( )
A.(-3,0) B.(0,12) C.(-12,0) D.(-60,-12)
7.已知函数f(x)=log2(x-1),则 ( )
A.f(3x)<f(32x) B.f(3x)>f(32x)
C.f(3x)=f(32x) D.不能确定f(3x)与f(32x)大小关系
8.函数y=2x3-3x2-12x+5在[0,3]上最大值和最小值分别是 ( )
A.5,-15 B.5,-4 C.-4,-15 D.5,-16
9.某种细菌开始有两个,1小时后分裂成4个并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1个……按照这个规律,10小时后细胞存活数是 ( )
A.1023 B.1025 C.1535 D.1537
10.已知θ∈[0,π],f(θ)=sin(cosθ)的最大值为a,最小值为b,g(θ)=cos(sinθ)的最大值为c,最小值为d,则 ( )
A.b<d<a<c B.d<b<c<a
C.b<d<c<a D.d<b<a<c
11.点P是曲线![]() 上移动,设点P处切线倾斜角为
上移动,设点P处切线倾斜角为![]() ,则
,则![]() 的取值范围是
的取值范围是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.已知x1是方程x+lgx=3的根,x2是方程x+10x=3的根,那末x1+x2的值为 ( )
A.6 B.3
C.2 D.1
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.(理)y=sinx在0≤x≤2π与x轴所围成图形的面积S=
(文)函数y=x3+x2-5x-5的单调减区间是
14.已知椭圆![]() 与双曲线
与双曲线![]() 有相同焦点,则实数t=
有相同焦点,则实数t=
15.给出以下命题①存在实数x使sinx+cosx=![]() ;②若α、β是第一象限角,且α>β,则cosα<cosβ;③函数y=sin(
;②若α、β是第一象限角,且α>β,则cosα<cosβ;③函数y=sin(![]() )是偶函数;④若cosαcosβ=1,则sin(α+β)=0;⑤将y=sin2x图象向左平移
)是偶函数;④若cosαcosβ=1,则sin(α+β)=0;⑤将y=sin2x图象向左平移![]() 个单位得到的是函数y=sin(
个单位得到的是函数y=sin(![]() )的图象,其中正确命题的序号是
)的图象,其中正确命题的序号是
16.已知奇函数满足f(x+1)=-f(x),当x∈(0,1)时,f(x)=2x,则x∈(-3,-2)时f(x)=
答 题 卡
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题
13. 14. 15. 16.
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤。
17.(本大题满分12分)设![]() 、
、![]() 是两个不共线的非零向量(t∈R)
是两个不共线的非零向量(t∈R)
①若![]() 与
与![]() 起点相同,t为何值时,
起点相同,t为何值时,![]() ,t
,t![]() ,
,![]() (
(![]() +
+![]() )三向量的终点在一直线上?
)三向量的终点在一直线上?
②若![]() =
=![]() 且
且![]() 与
与![]() 夹角为60°,那末t为何值时
夹角为60°,那末t为何值时![]() -t
-t![]() 的值最小?
的值最小?
18.(本小题满分12分)
设人的某一特征(如眼睛大小)是由他一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人是纯隐性,具有rd基因的人为混合性。纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问
(1)1个孩子有显性决定特征的概率是多少?
(2)2个孩子中至少有一个有显性决定的特征的概率是多少?
19.(本小题满分12分)
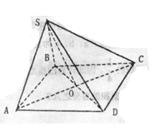
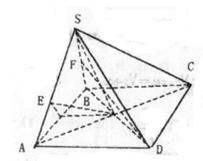
如图已知四棱锥S—ABCD底面是边长为a的正方形BD和AC相交于O,侧面SAB是正三角形且面SAB⊥面ABCD (1)求SO与面SAB所成之角;
(2)(理)求二面角B—SA—C; (文)求二面角B—SA—C的正切值;
(3)求点C到平面SBD的距离
|
20.(本小题满分12分)
已知等比数列{an}及等差数列{bn}其中b1=0,公差d≠0,将这两个数列对应项相加得一新数列1,1,2,……求这个新数列前10项之和。
21.(本小题满分12分)
某沿海城市计划今年起在江河入口处对一片滩涂每年都实行围垦造地。
(1)由于围垦土地势较低,为了防涝需购置设备建排水站所需经费与当年所围土地面积x(公项)的平方成正比,比例系数为a,又设围垦前每公顷面积的年平均收入为b元,围垦后每公顷面积的年平均收入为c元,那么为使所围垦面积的年收入不少于当年建设排水站的支出与围垦前的年收入之和,试求所围垦面积x(公顷)的最大值(a、b、c为常数).
(2)为了环保最终围垦造地的总面积不允许超过现有滩涂面积的![]() ,因此计划围垦造地的面积每年以1%的速度递减,问今年围垦面积最多只能占现有滩涂面积的百分之几?
,因此计划围垦造地的面积每年以1%的速度递减,问今年围垦面积最多只能占现有滩涂面积的百分之几?
22.(本小题满分14分)
已知点F(0,![]() ),上半平面内的点P到F和x轴的距离之和为
),上半平面内的点P到F和x轴的距离之和为![]()
(1)求动点P的轨迹;
(2)设动点P的轨迹是C1,曲线C1交y轴于M。A、B是曲线C1上满足∠AMB=![]()
的两点,证明直线AB与y轴交于一定点.
春考数学模拟试题
参考答案
一、 选择题
1.D 2.C 3.D 4.B 5.B 6.C 7.A 8.A 9.B 10.A 11.B 12.B
二、填空题13.(理)4 (文)(![]() ) 14.1 15.③④ 16.2-x-2
) 14.1 15.③④ 16.2-x-2
三、解答题17.①设![]() -t
-t![]() =m[
=m[![]() -
-![]() (
(![]() +
+![]() )](m∈R) 化简得
)](m∈R) 化简得![]()
![]() =
=![]()
![]()
∵![]() 与
与![]() 不共线 ∴
不共线 ∴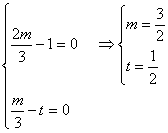
∴t=![]() 时,
时,![]() 、t
、t![]() 、
、![]() (
(![]() +
+![]() )终点在一直线上 ②
)终点在一直线上 ②![]() -t
-t![]() 2=(
2=(![]() -t
-t![]() )2=
)2=![]() 2+t2
2+t2![]() -2t,
-2t,
![]()
![]() cos 60°=(1+t2-t)
cos 60°=(1+t2-t)![]() 2, ∴t=
2, ∴t=![]() 时,
时,![]() -t
-t![]() 有最小值
有最小值![]()
18.孩子一对基因为dd,rr,rd的概率分别为![]() 孩子有显性决定特征具有dd或rd
孩子有显性决定特征具有dd或rd
(1)1个孩子有显性决定特征的概率为![]()
|
19.(1)在底面ABCD内作OH⊥AB于H,连SH ∵SAB⊥面ABCD
∴ OH⊥面SAB ∴∠OSH是SO与面SAB所成之角 ∵ABCD为
正方形 ∴OA=OB 又OH⊥AB ∴AH=BH 又△SAB是等边三
角形 ∴SH⊥AB SH=![]() 在Rt△SHO中 OH=
在Rt△SHO中 OH=![]()
∴![]() ∠OSH=
∠OSH=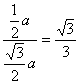 ∴∠OSH=30°,即SO与面SAB成30°角
∴∠OSH=30°,即SO与面SAB成30°角
(2)在面SAB内过H作HE⊥SA于E,连OE ∵OH⊥面SAB ∴OE⊥SA 则∠HEO是二面角B—SA—C的平面角,Rt△OHE中,HE=AHsin60°=![]() ∴二面角B—SA—C为arc tan
∴二面角B—SA—C为arc tan ![]()
tan∠HEO=![]() (3)∵SH⊥AB 而SAB⊥面ABCD ∴SH⊥面ABCD
(3)∵SH⊥AB 而SAB⊥面ABCD ∴SH⊥面ABCD
∴![]()
![]() ∵AD⊥AB AD⊥SH ∴AD⊥面SAB ∴AD⊥SA SD=
∵AD⊥AB AD⊥SH ∴AD⊥面SAB ∴AD⊥SA SD=![]() 在△SBD中取SB中点F连DF 则△SFD为Rt△且
在△SBD中取SB中点F连DF 则△SFD为Rt△且
DF=![]() 设点C到面SBD的距离为h
设点C到面SBD的距离为h
则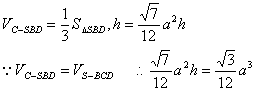
![]()
20.设等比数列首项为a,公比为q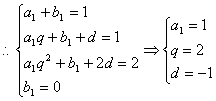
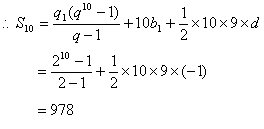
21.(1)围垦x公顷土地可得收入为cx元,故cx-(ax2+bx)≥0 即x[ax+(b-c)]≤0
当b≥c时,![]() ,不能围垦,当b<c时
,不能围垦,当b<c时 ![]() ,故围垦面积最大值为
,故围垦面积最大值为![]() (公顷)
(公顷)
(2)设该市现有滩涂面积为M公顷,今年围垦土地面积为x公顷,则x+x(1-1%)+x(1-1%)2+……≤![]()
![]() ,故今年所围垦面积最多只能是滩涂的0.25%.
,故今年所围垦面积最多只能是滩涂的0.25%.
22.设P到x轴距离为PQ ,P到直线![]() 的距离为PR.
的距离为PR.![]()
![]()
![]() ∴P的轨迹是以F(0,
∴P的轨迹是以F(0,![]() )为焦点
)为焦点
![]() 为准线的抛物线在上半平面的部分方程为
为准线的抛物线在上半平面的部分方程为![]()
(2)设A(x1,4-x) B(x2,4-x2 2 ) 又M(0,4)∴![]()
![]()
由x1≠x2得(x1+x2)x+y-3=0,它与y轴交点为(0,3)是一个定点.