高三第二次月考数学试题
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1．设x是纯虚数，y是实数，且
等于（ ）
A．
B
C．
D．1
2．数列
的前n项和为Sn，若
，则这个数列一定是 （ ）
A．等比数列 B．等差数列
C．从第二项起是等比数列 D．从第二项起是等差数列
3．设
，则n的值为（ ）
A．9 B．8 C．7 D．6
4．设集合A和B都是实数集，映射
把集合A中的元素x映射到集合B中的元素
，则在映射f下，象1的原象组成的集合是 （ ）
A．{1} B．{0，1，－1} C．{0} D．{0，－1，－2}
5．设
，那么
是 （ ）
A．奇函数且在（0，+∞）上是增函数 B．偶函数且在（0，+∞）上是减函数
C．奇函数且在（－∞，0）上是增函数 D．偶函数且在（－∞，0）上是减函数
6．假定从甲地到乙地通话x分钟的电话费
其中
是大于或等于x的最小整数，则从甲地到乙地通话时间5.5分钟的电话费为（ ）
A．3.71 B．3.97 C．4.24 D．4.77
7．若函数
是偶函数，则
的图象关于（ ）
A．直线
对称 B．直线
对称
C．直线
对称 D．y轴对称
8．设函数是定义在R上的奇函数，对于任意
，
.当
时
的值是（ ）
A．1 B．－1 C．
D．
9．不等式
的解集是
A．
B．
C．{
} D．
10．在（
）内，使
成立的x取值范围为
A．
B．
C．
D．
11．已知f（x）是奇函数，定义域为{xx∈R，x≠0}.又f（x）在区间（0，+∞）上是增函数，且f（－1）=0，则满足f（x）＞0的x的取值范围是 （ ）
A．（1，+∞） B．（0，1）
C．（－1，0）∪（1，+∞） D．（－∞，－1）∪（1，+∞）
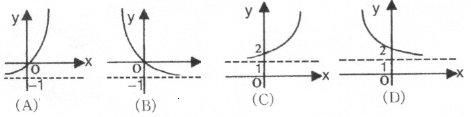
12．函数
的反函数的图象是 （ ）
第Ⅱ卷（非选择题共90分）
二、填空题：本大题共5小题，每小题5分，共25分.把答案填在题中横线上.
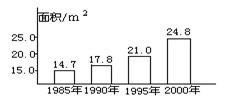13．据新华社2002年3月12日电，1985年到
2000年间，我国农村人均居住面积如图所
示，其中，从 年到 年的
五年间增长最快.
14．若集合
，则b=
15．对于给定的函数
，有下列结论：
①的图象关于原点对称； ②是R上的增函数
③
④有最小值0
其中正确命题的序号是 ①②④ .
16．如果
的值是 3/22 ．
17．设数列{an}的前n项和为
三、解答题：
18．（本小题满分12分）
|
.
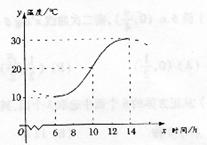
（Ⅰ）求这段时间的最大温差；
（Ⅱ）写出这段曲线的函数解析式.
19．本小题主要考查不等式的解法、对数函数的性质等基本知识，考查运算能力和逻辑思维能力. 满分12分.
解不等式
..
20．（本小题满分14分）
某租赁公司拥有汽车100辆. 当每辆车的月租金为3000元时，可全部租出. 当每辆车的月租金每增加50元时，未租出的车将会增加一辆. 租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.
（Ⅰ）当每辆车的月租金定为3600元时，能租出多少辆车？
（Ⅱ）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？
21．（本小题满分13分）
已知
.
（Ⅰ）化简f（x）的解析式；
（Ⅱ）若0≤θ≤π，求θ，使函数f（x）为偶函数；
（Ⅲ）在（Ⅱ）成立的条件下，求满足
的x的集合
22．（本小题满分14分）
设
.
求证：（1）数列{bn+2}是公比为2的等比数列； （2）
；
（3）
.
数学试题答案 03.9.16
一、选择题：
1． B ,2．A ,3．D ,B ,5．B．6．C．7．A．8．B．9．D． 10．C．11．C．12．C
二、填空题：
13．1995 ,2000,14．，2, 15． ①②④ 16． 3/22 17． 67
三、解答题：
18．
解：（Ⅰ）由图示，这段时间的最大温差是
30－10=20（℃）
（Ⅱ）图中从6时到14时的图象是函数的半个周期的图象，
由图示，
这时
将
综上，所求的解析式为
19．解：原不等式变形为.所以，原不等式
.
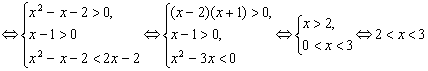故原不等式的解集为
.
20．解：（Ⅰ）当每辆车的月租金定为3600元时，未租出的车辆数为
，所以这时租出了88辆车.
（Ⅱ）设每辆车的月租金定为x元，则租赁公司的月收益为
，
整理得
.
所以，当x=4050时，最大，最大值为
，
即当每辆车的月租金定为4050元时，租赁公司的月收益最大，最大月收益为307050元.
21．解：（Ⅰ）
（Ⅱ）当
时，f（x）为偶函数
（Ⅲ）由
…12分
22．证明：（1）由
是公比为2的等比数列
（2）由（1）可知
令n=1，2，…n－1，
则
，各式相加
得
（3）
