高三第二学期数学练习卷
班级 学号 姓名 成绩
一. 填空题:本大题共12小题,每小题4分,共48分。
(1)当![]() 时,复数
时,复数![]() 在复平面上对应的点位于 象限。
在复平面上对应的点位于 象限。
(2)双曲线![]() 的渐近线方程是 。
的渐近线方程是 。
(3)在极坐标系中,圆心在![]() 且过极点的圆的方程为
。
且过极点的圆的方程为
。
(4)若![]() 为函数
为函数![]() 的反函数,则
的反函数,则![]() 的值域是_
_。
的值域是_
_。
(5)![]() 的值为____________。
的值为____________。
(6)在100件产品中有6件次品,现从中任取3件产品,至少有1件次品的不同取法的种数是(用式子表示) 。
(7)为使抛物线![]() 上的点P与A(0,-4)和点B(2,0)构成的△PAB的面积最小,P点的坐标应为
.
上的点P与A(0,-4)和点B(2,0)构成的△PAB的面积最小,P点的坐标应为
.
(8)已知点![]() 在直线
在直线![]() 、
、![]() 为常数)上,则
为常数)上,则![]() 的最小值为
.
的最小值为
.
(9)期中考试以后,班长算出了全班40个人数学成绩的平均分为M,如果把M当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为N,那么M:N为 。
(10)两个完全相同的长方体的长、宽、高分别为5cm,4cm,3cm,把它们重叠在一起组成一个新长方体,在这些新长方体中,最长的对角线的长度是 。
(11)据某校环保小组调查,某区垃圾量的年增长率为b,2003年产生的垃圾量为a吨。由此预测,该区下一年的垃圾量为__ __吨,2008年的垃圾量为 吨。
(12)若直线![]() 与圆
与圆![]() 没有公共点,则以(m,n)为点P的坐标,过点P的一条直线与椭圆
没有公共点,则以(m,n)为点P的坐标,过点P的一条直线与椭圆![]() 的点有______个。
的点有______个。
二. 选择题:(16分)
(13)在函数![]() 中,最小正周期为
中,最小正周期为![]()
的函数是 ( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
(14)将抛物线y2=2px先向左平移1个单位,再向上平移1个单位,所得到的抛物线的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(15)已知![]() ,则下列不等关系中必定成立的是 ( )
,则下列不等关系中必定成立的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(16)已知三个不等式:![]() (其中a,b,c,d均
(其中a,b,c,d均
为实数),用其中两个不等式作为条件,余下的一个不等式作为结论组成一个
命题,可组成的正确命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
三. 解答题:本大题共6小题,共86分。(12+12+14+14+16+18)
(17)若关于x的不等式![]() <0的解集为M,
<0的解集为M,
(1)当a=4时,求集合M. (2)若3ÎM且5 ÏM,求实数a的取值范围.
(18)在![]() 中,a,b,c分别是
中,a,b,c分别是![]() 的对边长,已知a,b,c成等比数列,且
的对边长,已知a,b,c成等比数列,且![]() ,求
,求![]() 的大小及
的大小及![]() 的值。
的值。
(19)已知点A(2,8),![]() 在抛物线
在抛物线![]() 上,
上,![]() 的重心与此抛物线的焦点F重合(如图)
的重心与此抛物线的焦点F重合(如图)
(I)写出该抛物线的方程和焦点F的坐标; (II)求线段BC中点M的坐标;
(III)求BC所在直线的方程。
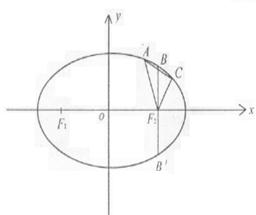
(20)已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且F1B+F2B=10.椭圆上不同的两点A(x1,y1)、C(x2,y2)满足条件:F2A、F2B、F2C成等差数列.
(I)求该椭圆的方程; (Ⅱ)求弦AC中点的横坐标.
(Ⅲ)设弦AC垂直平分线的方程为y=kx+m,求m的取值范围.
(21)某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元。
(I)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(II)设一次订购量为x个,零件的实际出厂单价为P元,写出函数![]() 的表达式;
的表达式;
(Ⅲ)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
(22)下表给出一个“等差数阵”:
| 4 | 7 | ( ) | ( ) | ( ) | …… |
| …… |
| 7 | 12 | ( ) | ( ) | ( ) | …… |
| …… |
| ( ) | ( ) | ( ) | ( ) | ( ) | …… |
| …… |
| ( ) | ( ) | ( ) | ( ) | ( ) | …… |
| …… |
| …… | …… | …… | …… | …… | …… | …… | …… |
|
|
|
|
|
| …… |
| …… |
| …… | …… | …… | …… | …… | …… | …… | …… |
其中每行、每列都是等差数列,![]() 表示位于第i行第j列的数。
表示位于第i行第j列的数。
(I)写出![]() 的值; (II)写出
的值; (II)写出![]() 的计算公式;
的计算公式;
(III)证明:正整数N在该等差数列阵中的充要条件是2N+1可以分解成两个不是1的正整数之积。
高三第二学期数学练习卷
【试题答案】参考解答
一. 填空题:本大题共12小题,每小题4分,共48分。
(1)当![]() 时,复数
时,复数![]() 在复平面上对应的点位于 第四 象限。
在复平面上对应的点位于 第四 象限。
(2)双曲线![]() 的渐近线方程是
的渐近线方程是 ![]() 。
。
(3)在极坐标系中,圆心在![]() 且过极点的圆的方程为
且过极点的圆的方程为![]() 。
。
(4)若![]() 为函数
为函数![]() 的反函数,则
的反函数,则![]() 的值域是_
的值域是_![]() _。
_。
(5)![]() 的值为____1________。
的值为____1________。
(6)在100件产品中有6件次品,现从中任取3件产品,至少有1件次品的不同
取法的种数是(用式子表示) ![]() 。
。
(7)为使抛物线![]() 上的点P与A(0,-4)和点B(2,0)构成的△PAB的面积最小,P点的坐标应为 (1,1) .
上的点P与A(0,-4)和点B(2,0)构成的△PAB的面积最小,P点的坐标应为 (1,1) .
(8)已知点![]() 在直线
在直线![]() 、
、![]() 为常数)上,则
为常数)上,则![]() 的最小值为
的最小值为 ![]() .
.
(9)期中考试以后,班长算出了全班40个人数学成绩的平均分为M,如果把M
当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均
值为N,那么M:N为 1 。
(10)两个完全相同的长方体的长、宽、高分别为5cm,4cm,3cm,把它们重叠在
一起组成一个新长方体,在这些新长方体中,最长的对角线的长度是
![]()
(11)据某校环保小组调查,某区垃圾量的年增长率为b,2003年产生的垃圾量为a吨。由此预测,该区下一年的垃圾量为__![]() __吨,2008年的垃圾量为
__吨,2008年的垃圾量为![]() 吨。
吨。
(12)若直线![]() 与圆
与圆![]() 没有公共点,则以(m,n)为点P的坐标,过点P的一条直线与椭圆
没有公共点,则以(m,n)为点P的坐标,过点P的一条直线与椭圆![]() 的公共点有_____2____个。
的公共点有_____2____个。
二. 选择题:(16分)
(13)在函数![]() 中,最小正周期为
中,最小正周期为![]()
的函数是 ( A )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
(14)将抛物线y2=2px先向左平移1个单位,再向上平移1个单位,所得到的抛物线的方程为( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(15)已知![]() ,则下列不等关系中必定成立的是 ( B )
,则下列不等关系中必定成立的是 ( B )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(16)已知三个不等式:![]() (其中a,b,c,d均
(其中a,b,c,d均
为实数),用其中两个不等式作为条件,余下的一个不等式作为结论组成一个
命题,可组成的正确命题的个数是 ( D )
A. 0 B. 1 C. 2 D. 3
三. 解答题:本大题共6小题,共84分。解答应写出文字说明,证明过程或演算步骤。
(17)若关于x的不等式![]() <0的解集为M,
<0的解集为M,
(1)当a=4时,求集合M. (2)若3ÎM且5 ÏM,求实数a的取值范围.
解: (1)(-¥,-2)È (![]() ,2)
,2)
(2)[1,+![]() )È(9,25] .
)È(9,25] .
(18)解:(I)![]() 成等比数列
成等比数列 ![]() 又
又![]()
![]() 在
在![]() 中,由余弦定理得
中,由余弦定理得
![]()
![]()
(II)解法一:在![]() 中,由正弦定理得
中,由正弦定理得![]()
![]()
![]()
解法二:在![]() 中,由面积公式得
中,由面积公式得![]()
![]()
(19) 解:(I)由点A(2,8)在抛物线![]() 上,有
上,有![]() 解得
解得![]()
所以抛物线方程为![]() ,焦点F的坐标为(8,0)
,焦点F的坐标为(8,0)
(II)如图,由F(8,0)是![]() 的重心,M是BC的中点,所以F是线段AM的定比分点,且
的重心,M是BC的中点,所以F是线段AM的定比分点,且![]() 设点M的坐标为
设点M的坐标为![]() ,则
,则
![]() 解得
解得![]() 所以点M的坐标为
所以点M的坐标为![]()
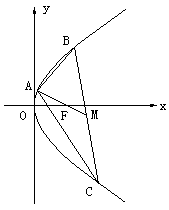
(III)由于线段BC的中点M不在x轴上,所以BC所在的直线不垂直于x轴。
设BC所成直线的方程为
![]() 由
由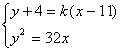 消x得
消x得
![]() 所以
所以![]()
由(II)的结论得![]() 解得
解得![]()
因此BC所在直线的方程为 ![]() 即
即![]()
20.本小题主要考查直线与椭圆等基本知识,考查综合运用数学知识和方法分析解决问题
的能力.(I)解:由椭圆定义及条件知
|
所以 ![]() 故椭圆方程为
故椭圆方程为![]()
(Ⅱ)由点B(4,yB)在椭圆上,得 F2B=yB=![]()
解法一:
因为椭圆右准线方程为![]() ,离心率为
,离心率为![]() .
.
根据椭圆定义,有F2A=![]() , F2C=
, F2C=![]() .
.
由F2A,F2B,F2C成等差数列,得 ![]()
由此得出x1+x2=8.
设弦AC的中点为P(x0,y0), 则 ![]()
解法二:
由F2A,F2B,F2C成等差数列,得
![]() ①
①
由A(x1,y1)在椭圆![]() 上,得
上,得 ![]()
所以![]()
![]() .
②
.
②
同理可得![]() ③
③
将②、③代入①式,得 ![]() 所以x1+x2=8.
所以x1+x2=8.
设弦AC的中点为P(x0,y0), 则![]()
(Ⅲ)解法一:
|
![]()
由④-⑤得 ![]()
即![]()
将![]() 代入上式,得
代入上式,得
![]()
由上式得 ![]() (当k=0时也成立).
(当k=0时也成立).
由点P(4,y0)在弦AC的垂直平分线上,得
y0=4k+m, 所以![]()
由P(4,y0)在线段BB'(B'与B关于x轴对称,如图)的内部,得
![]() <y0<
<y0<![]() , 所以
, 所以 ![]() <m<
<m<![]() .
.
注:在推导过程中,未写明“x1≠x2”、“k≠0”、“k=0时也成立”及把结论写为
“![]() ≤m≤
≤m≤![]() ”的均不扣分.
”的均不扣分.
解法二:
因为弦AC的中点为P(4,y0),
所以直线AC的方程为![]() ⑥
⑥
将⑥代入椭圆方程![]() 得
得
![]()
所以![]() 解得
解得![]() (当k=0时也成立).
(当k=0时也成立).
以下步骤同解法一.
(21)解:(I)设每个零件的实际出厂价恰好降为51元时,一次订购量为![]() 个,则
个,则
![]()
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元。
(II)当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以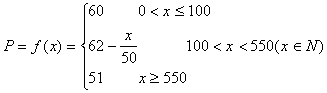
(III)设销售商的一次订购量为x个时,工厂获得的利润为L元,则
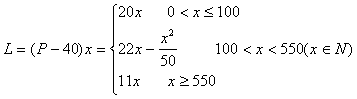
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;
如果订购1000个,利润是11000元。
(22)本小题主要考查等差数列、充要条件等基本知识,考查逻辑思维能力、分析问题和解决问题的能力。
解:(I)![]()
(II)该等差数阵的第一行是首项为4,公差为3的等差数列:
![]()
第二行是首项为7,公差为5的等差数列:
![]()
……
第i行是首项为![]() ,公差为
,公差为![]() 的等差数列,因此
的等差数列,因此
![]()
(III)必要性:若N在该等差数阵中,则存在正整数i,j使得![]()
从而![]()
![]()
即正整数2N+1可以分解成两个不是1的正整数之积。
充分性:若2N+1可以分解成两个不是1的正整数之积,由于2N+1是奇数,则它必为两个不是1的奇数之积,即存在正整数k,l,使得
![]()
从而![]()
可见N在该等差数阵中
综上所述,正整数N在该等差数阵中的充要条件是2N+1可以分解成两个不是1的正整数之积。
(19)设点![]() 到点
到点![]() 、
、![]() 距离之差为
距离之差为![]() ,到
,到![]() 、
、![]() 轴的距离之比为2,求
轴的距离之比为2,求![]() 的取值范围。(2002全国)
的取值范围。(2002全国)

22。已知抛物线![]() .过动点M(
.过动点M(![]() ,0)且斜率为1的直线
,0)且斜率为1的直线![]() 与该抛物线交于不同的两点A、B,
与该抛物线交于不同的两点A、B,![]() .
.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)若线段AB的垂直平分线交![]() 轴于点N,求
轴于点N,求![]() 面积的最大值.(2001北京春)_
面积的最大值.(2001北京春)_
解:(Ⅰ)直线![]() 的方程为
的方程为![]() ,将
,将 ![]() ,
,
得 ![]() . ……2分
. ……2分
设直线![]() 与抛物线两个不同交点的坐标为
与抛物线两个不同交点的坐标为![]() 、
、![]() ,
,
则 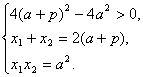 ……4分
……4分
又![]() ,
,
∴ ![]()
![]()
![]() .……6分
.……6分
∵ ![]() ,∴
,∴
![]() .解得
.解得 ![]() . ……8分
. ……8分
(Ⅱ)设AB的垂直平分线交AB于点Q,令坐标为![]() ,则由中点坐标公式,得
,则由中点坐标公式,得![]() ,
,
![]() . …10分
. …10分
∴
![]() .
.
又
![]() 为等腰直角三角形,∴
为等腰直角三角形,∴
![]() ,
,
∴
![]() . ……12分
. ……12分
![]()
即![]() 面积最大值为
面积最大值为![]() ……14分
……14分
21.本题共有2个小题,第1小题满分9分,第2小题满分7分
已知椭圆C的方程为![]() ,点
,点![]() 的坐标满足
的坐标满足![]() ≤1.过点P的直线
≤1.过点P的直线![]() 与椭圆交于A、B两点,点Q为线段AB的中点.求:
与椭圆交于A、B两点,点Q为线段AB的中点.求:
(1)点Q的轨迹方程;
(2)点Q的轨迹与坐标轴的交点的个数.(上海2001春)
[解](1)设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,设直线
时,设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 的方程为
的方程为![]() .
.
由已知![]() ,
①
,
①
![]() ,
②
,
②
由①得![]() , ③
, ③
由②得![]() ,
④由③、④及
,
④由③、④及![]() ,得点
,得点![]() 的坐标满足方程
的坐标满足方程
![]() .
⑤
.
⑤
当![]() 时,
时,![]() 不存在,此时
不存在,此时![]() 平行于
平行于![]() 轴,因此
轴,因此![]() 的中点
的中点![]() 一定落在
一定落在![]() 轴上,即
轴上,即![]() 的坐标为(
的坐标为(![]() ).显然点
).显然点![]() 的坐标满足方程⑤.
的坐标满足方程⑤.
综上所述,![]() 的坐标满足方程
的坐标满足方程 ![]() .
.
设方程⑤所表示的曲线为![]() ,则由
,则由
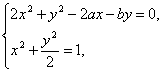 得
得 ![]() .
.
因为![]() ,由已知
,由已知![]() ≤1,所以当
≤1,所以当![]() =1时,
=1时,![]() ,曲线
,曲线![]() 与椭圆
与椭圆![]() 有且只有一个交点
有且只有一个交点![]() .
.
当![]() <1时,
<1时,![]() ,曲线
,曲线![]() 与椭圆
与椭圆![]() 没有交点.
没有交点.
因为(0,0)在椭圆![]() 内,又在曲线
内,又在曲线![]() 上,所以曲线
上,所以曲线![]() 在椭圆
在椭圆![]() 内.故点
内.故点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)由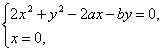 解得曲线
解得曲线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、
![]() .
.
由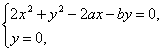 解得曲线
解得曲线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() .
.
当![]() ,即点
,即点![]() 为原点时,
为原点时,![]() 、
、![]() 与
与![]() 重合,曲线
重合,曲线![]() 与坐标轴只有一个交点
与坐标轴只有一个交点![]() .
.
当![]() ,且
,且![]() ≤
≤![]() ,即点
,即点![]() 不在椭圆
不在椭圆![]() 外且在除去原点的
外且在除去原点的![]() 轴上时,点
轴上时,点![]() 与
与![]() 重合,曲线
重合,曲线![]() 与坐标轴有两个交点
与坐标轴有两个交点![]() 与
与![]() .
.
同理,当![]() ,且
,且![]() ≤1,即点
≤1,即点![]() 不在椭圆
不在椭圆![]() 外且在除去原点的
外且在除去原点的![]() 轴上时,曲线
轴上时,曲线![]() 与坐标轴有两个交点
与坐标轴有两个交点![]() 与
与![]() .
.
当![]() <1,且
<1,且![]()
![]() ,即点
,即点![]() 在椭圆
在椭圆![]() 内且不在坐标轴上,曲线
内且不在坐标轴上,曲线![]() 与坐标轴有三个交点
与坐标轴有三个交点![]() 、
、![]() 与
与![]() .
.
22.(本小题满分13分)(2003北京春)
已知动圆过定点P(1,0),且与定直线![]() 相切,点C在l上.
相切,点C在l上.
(Ⅰ)求动圆圆心的轨迹M的方程;
(Ⅱ)设过点P,且斜率为-![]() 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.
(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
解:(Ⅰ)依题意,曲线M是以点P为焦点,直线l为准线的抛物线,所以曲线M的方程为![]() .
.
(Ⅱ)(i)由题意得,直线AB的方程为
![]() 消y得
消y得
![]()
所以A点坐标为![]() ,B点坐标为(3,
,B点坐标为(3,![]() ),
),
![]()
假设存在点C(-1,y),使△ABC为正三角形,则BC=AB且AC=AB,即
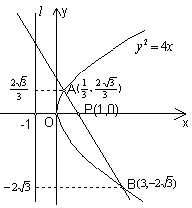
|
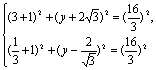
由①-②得
![]()
![]()
但![]() 不符合①,
不符合①,
所以由①,②组成的方程组无解.
因此,直线l上不存在点C,使得△ABC是正三角形.
(ii)解法一:设C(-1,y)使△ABC成钝角三角形,
由![]() ,
,
即当点C的坐标为(-1,![]() )时,A,B,C三点共线,故
)时,A,B,C三点共线,故![]() .
.
又![]() ,
,
![]() ,
,![]() .
.
当![]() ,即
,即![]() ,
,
即![]() 为钝角.
为钝角.
当![]() ,即
,即![]() ,
,
即![]() 为钝角.
为钝角.
又![]() ,即
,即![]() ,
,
即![]() . 该不等式无解,所以∠ACB不可能为钝角.
. 该不等式无解,所以∠ACB不可能为钝角.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是![]() .
.
解法二:
以AB为直径的圆的方程为![]() .
.
圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以,以AB为直径的圆与直线l相切于点G![]() .
.
当直线l上的C点与G重合时,∠ACB为直角,当C与G 点不重合,且A,B,C三点不共线时, ∠ACB为锐角,即△ABC中∠ACB不可能是钝角.
因此,要使△ABC为钝角三角形,只可能是∠CAB或∠CBA为钝角.
过点A且与AB垂直的直线方程为![]() .
.
过点B且与AB垂直的直线方程为![]() .
.
令![]() .
.
又由![]() ,所以,当点C的坐标为(-1,
,所以,当点C的坐标为(-1,![]() )时,A,B,C三点共 线,不构成三角形.
)时,A,B,C三点共 线,不构成三角形.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是![]()