高考数学仿真试题(三)A答案
一、1.D 2.B 3.A 4.B 5.B 6.C 7.D 8.C9.C 10.A 11.B 12.B
二、13.［-2,
］ 14. 1 15. 21 16.②③
三、17.解：原方程可化为loga(x2-x-2)=loga(ax-2) 2分
|
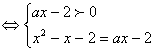4分
由②得x=a+1或x=0,当x=0时，原方程无意义，舍去. 8分
当x=a+1由①得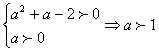
10分
∴a＞1时，原方程的解为x=a+1 12分
18.解：(Ⅰ)设{an}首项为a1,公差为d,
则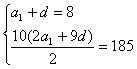
,解得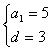
∴an=5+3(n-1),即an=3n+2 6分
（Ⅱ）设b1=a2,b2=a4,b3=a8,
则bn=a2n=3×2n+2
∴An=(3×2+2)+(3×22+2)+…+(3×2n+2)
=3×(2+22+…+2n)+2n
=3×
+2n=6×2n-6+2n 12分
19.（Ⅰ）证明：在Rt△ABC中，∠C=30°，D为AC的中点，则△ABD是等边三角形
又E是BD的中点，∵BD⊥AE，BD⊥EF，
折起后，AE∩EF=E，∴BD⊥面AEF
∵BD
面BCD，∴面AEF⊥面BCD 6分
（Ⅱ）解：过A作AP⊥面BCD于P，则P在FE的延长线上，设BP与CD相交于Q，令AB=1，则△ABD是边长为1的等边三角形，若AB⊥CD，则BQ⊥CD
,又AE=
∴折后有cosAEP=
由于∠AEF=θ就是二面角A—BD—C的平面角，
∴当θ＝π-arccos
时，AB⊥CD 12分
20.解：（Ⅰ）第n年共有5n个职工，那么基础工资总额为5n(1+
)n（万元）
医疗费总额为5n×0.16万元，房屋补贴为
5×0.04+5×0.04×2+5×0.04×3+…+5×0.04×n=0.1×n(n+1)（万元） 2分
∴y=5n(1+)n+0.1×n(n+1)+0.8n
=n［5(1+)n+0.1(n+1)+0.8］（万元） 6分
（Ⅱ）5(1+)n×20%-［0.1(n+1)+0.8］
=(1+)n-(n+9)
=［10(1+)n-(n+9)］
∵10(1+)n=10(1+Cn1Cn1+Cn2
+…)
＞10(1+
)＞10+n＞n+9
故房屋补贴和医疗费总和不会超过基础工资总额的20% 12分
21.解：（Ⅰ）由抛物线y2=2x-4,即y2=2 (x-
),可知抛物线顶点为（,0）,准线方程为x=
.
在双曲线C中，中心在原点，右焦点（，0），右准线x=,
∴
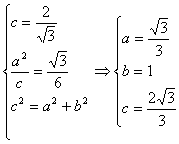
∴双曲线c的方程3x2-y2=1 4分
（Ⅱ）由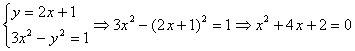
∴AB=2
8分
（Ⅲ）假设存在实数k,使A、B关于直线y=ax对称，设A(x1,y1)、B(x2,y2),
|
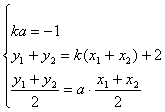
由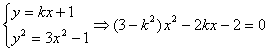
④
由②③，有a(x1+x2)=k(x1+x2)+2 ⑤
由④知：x1+x2=
代入⑤
整理得ak=3与①矛盾，故不存在实数k，使A、B关于直线y=ax对称. 12分
22.（Ⅰ）证明：因f(m1),f(m2)满足a2+［f(m1)+f(m2)］a+f(m1)f(m2)=0
即［a+f(m1)］［a+f(m2)］=0
∴f(m1)=-a或f(m2)=-a,
∴m1或m2是f(x)=-a的一个实根，
∴Δ≥0即b2≥4a(a+c).
∵f(1)=0,∴a+b+c=0
且a＞b＞c,∴a＞0,c＜0,
∴3a-c＞0,∴b≥0 5分
(Ⅱ)证明：设f(x)=ax2+bx+c=0两根为x1,x2,则一个根为1，另一根为
,
又∵a＞0,c＜0，
∴＜0,
∵a＞b＞c且b=-a-c≥0,
∴a＞-a-c＞c,∴-2＜≤-1
2≤x1-x2＜3 10分
（Ⅲ）解：设f(x)=a(x-x1)(x-x2)=a(x-1)(x-)
由已知f(m1)=-a或f(m2)=-a
不妨设f(m1)=-a则a(m1-1)(m1-)=-a＜0,
∴＜m1＜1
∴m1+3＞+3＞1
∴f(m1+3)＞f(1)＞0
∴f(m1+3)＞0 12分
同理当f(m2)=-a时，有f(m2+3)＞0,
∴f(m2+3)或f(m1+3)中至少有一个为正数 14分