高考数学模拟试卷2
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，
只有一项是符合题目要求的，请将所选答案填在题后括号内。
1、函数
的最小正周期是( )
A、
B、2
C、
D、4
2、命题“若A
B，则A=B”与逆命题、否命题、逆否命题共四个命题中，真命题的个数有( )
A、4 B、3 C、2 D、0
3、在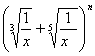
的展开式中，所有奇数项系数之和等于1024，则中间项系数是( )
A、330 B、462 C、682 D、792
4、已知直线l：
,则直线1的倾斜角为( )
A、
B、－
C、
D、
5、已知椭圆
，点P是椭圆上一点，F1、F2是椭圆的左、右焦点，则PF1中点M的轨迹是( )
A、圆 B、椭圆 C、双曲线 D、抛物线
6、在△ABC中，若
，则△ABC为( )
A、正三角形 B、直角三角形 C、等腰三角形 D、无法确定
7、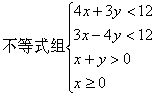
表示的平面区域内的整点(横坐标和纵坐标都是整数的点)个数是( )
A、7 B、9 C、10 D、11
8、已知正方形ABCD，沿对角线AC将△ABC折起，设AD与平面ABC所成角为α，当α取最大值时，二面角B－AC－D等于( )
A、90°
B、60°
C、45°
D、
9、把函数
的图象沿向量
平移后，得到函数
的图象，则的坐标为( )
A、
B、
C、
D、
10、不等式
的解集是
，则a的值等于( )
A、1 B、2 C、3 D、4
11、若
能被31整除(n∈N+)，则最小非负整数a的值为( )
A、0 B、1 C、2 D、4
12、某住宅小区有居民2万户，从中随机抽取200户，调查是否安装电话，调查的结果如下：
| 电话 | 动迁户 | 原住户 |
| 已安装 | 65 | 30 |
| 未安装 | 40 | 65 |
则该小区已安装电话的户数估计有( )
A、6500 B、300 C、19000 D、9500
二、填空题：本大题4小题，每小题4分，共16分。把答案填在题中横线上。
13、函数
的最大值为7，最小值为1，则曲线
的离心率为
____________________。
14、在研究试验中发现，一种放射性元素经过100年剩留原来质量的a%(0<a<100)，则质量为b的这种元素经过25年的剩留为__________(规定：每年的衰变率保持不变)
15、在区间
上，函数
在同一点取得相同的最大值，那么f(x)在区间
上的最小值是______________。
16、已知点P是抛物线y2=4x上一点，设P到此抛物线准线距离为d1,到直线x+2y－12=的距离为d2，则d1+d2的最小值是__________________。
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17、(本题12分)已知
(1)
求证：
(2)
将tan
表示成tan的函数关系式。
(3) 求tanβ的最大值，并求当tanβ取得最大值时tan(α+β)的值。
18、(本小题12分)已知直三棱柱ABC-A1B1C1中，AC1⊥A1B，B1C1=A1C1，M是A1B1的中点。
(1) 求证：A1B⊥AM
(2) 若AA1=1，∠A1C1B1=90°，求二面角C1-AB-C的平面角的正切值。
(3) 在(2)的条件下，求三棱锥A-A1BC1的体积。
19、(本小题12分)某市环保部门对城市里一条污水河进行改造，即用隔离物将其封闭，封闭物横截面为对称的抛物线段(如图)，封闭处污水河面宽AB为10米，隔离物最高点O到污水河面的距离为2米，当外围水域涨水时，污水河面随之升高。
(1) 当污水河面上升1米时，求此时河面宽；
(2)
当上升水面宽为a米时，增加部分的污水横截面积等于
平方米，若污水以0.5米/秒流动时，求(1)中每小时增加的污水量。(精确到1立方米)
20、(本小题12分)设一台机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作，一周5个工作日里无故障可获利润10万元，发生一次故障可获利5万元，发生两次故障没有利润，发生三次或三次以上故障就亏损2万元，求一周内平均获利多少？
21、(本小题12分)是否存在等差数列
使得
？若存在，求出其通项公式；若不存在，请说明理由。
22、(本小题14分)已知曲线c1的方程为xy=－1,曲线c1关于点M
的对称曲线为c2, (1)求曲线c2的表达式y=f(x)，并求出y=f(x)的单调区间。
(2)若
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 13 |
| 答案 | B | C | B | D | B | C | A | A | D | C | B | D |
二、填空题
13、
14、
15、
16、
三、解答题
17、解：
(1)
由已知，得
…2分
进一步，得
∴…………………………………………………………4分
(2)
……………………6分
(3)
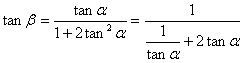………………………………………8分
∵
∴
………………………………………………………10分
当且仅当
时取“=”号，因此当
时，
取最大值
时，此时
………12分
(参考第一册(下)P91 9)
18、(1)
…………………………………………………………………………………2分
又∵AC1⊥A1B，∴A1B⊥平面AC1M，A1B⊥AM…………………………… 4分
(2)解：∵△A1 AM∽△ABA1
∴
…………………………………………… 6分
∵△ABC为等腰直角三角形，取AB的中点N，连CN、C1N，则
∠C1NC 即为二面角C1—AB—C的平面角，易求得
…8分
(3)解：
………………… 12分
19、解：(1)如图建立直角坐标系
设抛物线方程y=ax2，把(5，－2)代入，
得
∴y=
…………………4分
当y=－1时,
…………6分
(2)
因为上升水面宽为
米，由题意得增加污水横截面积为
=
(平方米) ……………………………… …9分
所以每小时增加污水量为
(立方米) …12分
20、解：ξ表示一周内机器发生故障的次数，则
……………………… 2分
以η表示一周内所获的利润(η也是随机变量)，则
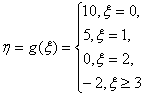……………………………………………4分
∴
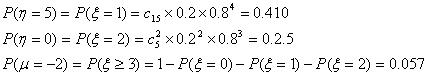
……………………………………………8分
∴Eη=10×0.325+5×0.410+0×0.205+(－2)×0.057=5.216
即一周内平均获利5.216万元。…………………………………………12分
21、解：假设存在这样的等差数列，设等差数列的通项公式为
，
其中a1、d分别为首项和公差，则
=
=
……………… 4分
∴
=
=
=
……………(1)
而
……………………………(2)
……………………………8分
比较(1)、(2)两式对应项的系数得
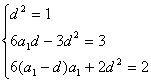解得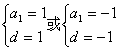
∴
由此可知，存在满足条件的等差数列,其通项公式是
……………12分
(本题是根据一道常见习题：“求和n·1+(n－1)·2+(n－2)·3+…+2·(n－1)+1·n”改编而成的)
22、简解：
(1)易求出曲线的C2表达式
，………………………………4分
可证 
在(－∞，－1)以及(－1，+∞)这两个区间上的单调递增………………6分
(2)∵
∴
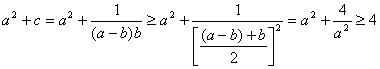
又
∴
而
∴
……………………………………………………14分
(源于教材第二册(上)P234和P313)