高考数学模拟试卷6
一、选择题:本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．不等式
的解集是
（
）
A．{xx＜1
B. {xx＞3或x＜1 C.{xx＞3} D. {x1＜x＜3
2．若指数函数y=f(x)的反函数的图象经过点（2，-1），则此指数函数是 （ ）．
A. y=
B. y=2x C.
y=3x
D. y=10x
3．中心在原点，准线方程为x = ±4，离心率为
的椭圆方程为
（
）
A. 
B.
C. 
D.
4．函数y=2sinxcosx －2sin2x＋１的最小正周期为 （ ）
A. 
B.
C. π
D. 2π
5．如果x,y是实数，那么xy＞0是
＝
＋
的
（ ）
Ａ.充分不必要条件 Ｂ.必要不充分条件
Ｃ.充要条件 Ｄ．既不充分又不必要条件
6.已知非负实数x,y满足2x+3y-8≤0且3x+2y-7≤0,则x+y的最大值是 （ ）
A．
B．
C．3
D．2
7.拟定从甲地到乙地通话m分钟的话费由f(x)=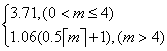
给出，其中
是大于或等于m的最小正整数，如:
=3,
=4,则从甲地到乙地通话5.2分钟的话费是
（ ）
A．3.71 B．4.24 C．4.77 D．7.95
8.已知数列1，a1,a2,4成等差数列,1，b1，b2，b3，4成等比数列，则
的值（ ）
A．
B．
C．或
D．
9． 对一切实数x，不等式x4＋ax2＋1≥0恒成立，则实数a的取值范围是 （ ）
A. （－∞，－2） B.
［－2，＋∞
C. ［0，2］
D. ［0，＋∞
10．已知函数f(x)及函数g(x)的图象分别如图⑴、⑵所示，则函数y=f(x)·g(x)的图
象大致是（ ）
A B C D
11. 已知
＝２，
=3,
与
的夹角60
,
=5+3,
=3+k,若⊥
,则k的值为
( )
A．-1
B．
D．
12.从集合{1,2,3,4,5,6,7,8,8,10}中选出5个数的子集中任何两个数的和均不等于11,则这样的子集合共有 ( )
A．10个 B．16个 C．20个 D．32个
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中的横线上。
13．二项式(x - 1)9的展开式中第5项的系数为 （用数字作答）
14．与直线2x-y-4=0平行且与曲线y=x2相切的直线方程是 .(用一般式表示)
15.将函数y=sin2x的图象按向量
=(
,2)平移,则平移后的图象所对应的函数
解析式是 .
16.不等式组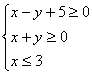
表示的平面区域的面积是
.
三、解答题（本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。）
17.（本题满分10分）已知:cos
=
,
＜＜
,求tan(2-)的值.
18．(本题满分10分)已知数列
成等差数列，
表示它的前
项和，
且
，
.
⑴求数列的通项公式
；
⑵数列
中，从第几项开始(含此项)以后各项均为正数？
注意：考生在（19甲）、（19乙）两题中选一题作答，如果两题都答，只以（19甲）计分。
（19甲）（本题满分14分）如图，PA⊥矩形ABCD所在平面，PA=AD=a，M，N分别是AB，PC的中点。
（1）求证：平面MND⊥平面PCD；
（2）若AB=
，求二面角N-MD-C的大小。
（19乙）（本题满分14分）如图，四棱锥P-ABCD中，侧面PDC是边长为2的正三角形且与底面垂直，底面为面积是
的菱形，∠ADC为锐角。
（1）求证：PA⊥CD；
（2）求二面角P-AD-C的正切值；
（3）试作出过P点的平面α，使平面α平面PBD垂直
(要求写出作图过程并加以证明)
20．（本题满分12分）猎人射击距离100米远处的目标，命中的概率为0.6。
（1）如果猎人射击距离100米远处的静止目标3次，求至少有一次命中的概率；
（2）如果猎人射击距离100米远处的动物，假如第一次未命中，则进行第二次射击，但由于枪声惊动动物使动物逃跑从而使第二次射击时动物离猎人的距离变为150米，假如第二次仍未命中，则必须进行第三次射击，而第三次射击时动物离猎人的距离为200米。假如击中的概率与距离成反比，。求猎人最多射击三次命中动物的概率。
21．（本题满分14分）如图，已知A，B，C是长轴长为4的椭圆上的三点，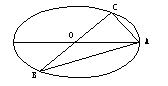
点A是长
轴的一个端点，BC过椭圆中心O，且满足AC⊥BC，BC=2AC.
⑴ 建立适当的坐标系，求椭圆的方程；
⑵ 如果P、Q是该椭圆上异于A、B的两点，使∠PCQ的平分线垂直于OA，
求证：PQ∥AB.
22. （本题满分14分）已知a＞0,函数y=f(x)=x3
–ax在x∈
是一个单调函
数，
⑴ 试问函数y=f(x)在a＞0的条件下，在x∈上能否是单调递减函数？请说
明理由；
⑵ 若f(x)在区间上是单调递增函数，试求出实数a的取值范围；
⑶ 设x0≥1，f(x0)≥1且f[f(x0)]=x0，求证：f(x0)=x0.
高三数学试卷参考答案
一．选择题：（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | C | C | A | C | B | A | B | B | C | D |
二．填空题（每小题4分，共16分）
13．126
14.2x-y-1=0
15.y=-cos2x+2
16.
三.解答题
17. （本小题满分10分）
∵ cos=,＜＜,∴ tan=
，
∴ 
，
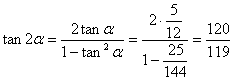∴tan(2-)=
=
.
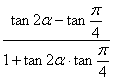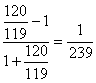18．（本小题满分10分）
⑴设数列的公差为，由已知
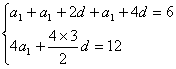
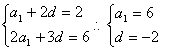
⑵
解不等式
，得
∵
，∴
∴
，或
故从第8项开始以后各项均为正数.
(19甲). （本小题满分14分）
（1）∵M、N分别是AB、PC的中点，可得
,
由于
,
及
,
∴MN⊥CD,又MN⊥DP, ∴MN⊥平面PCD, ∴平面MND⊥平面PCD.
（2）底面的法向量为
，设平面MN的法向量为
,
,∴
.
,∴
.
∴
,
∴
,
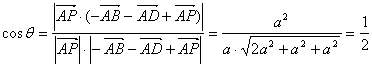∴二面角N-MD-C的大小为60°.
(19乙). （本小题满分14分）
（1）过点A作AH⊥CD,因为面积为,所以AH为
,DH为1,故H为DC的中点,三角形PDC为正三角形，PH⊥DC，所以DC⊥平面PAH，PA⊥CD
（2）过H作HE⊥AD，连接PH，则∠PEH为二面角的平面角，正切值为2.
（3）略
20．（本小题满分12分）
（1）记事件“猎人射击距离100米远处的静止目标3次，至少有一次命中”为A事件，
则P(A)=1-P(
)=1-0.4×0.4×0.4=0.936.
（2）记事件“第
次击中动物”为事件
（ =1,2,3），记事件“最多射击3次而击中动物”为事件B.
由条件P(B1)=0.6, P(B1)=
=0.4, P(B1)=
=0.3,
∵
,且是相互独立事件,又
、
、
是互斥事件，
∴
=0.832.
21．（本小题满分14分）
以O为坐标原点，OA所在直线为x轴，建立直角坐标系.
由题意，可设椭圆方程为
.
∵AC⊥BC，BC=2AC，OA =2，∴点C的坐标为（1，1）.
将C点的坐标代入椭圆方程，
，∴
.
∴椭圆方程为
.
⑵ 如图，设CP、CQ与x轴的交点为E、F，由题意知，∠CEF=∠CFE，从而直线CP与
CQ的斜率互为相反数，设直线CP的方程为y-1=k（x-1）（k≠0），则直线CQ的方程为
y-1=-k（x-1）.
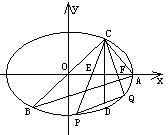设P（
，
），Q（
，
）
将直线CP的方程代入椭圆方程，化简得，
则
，∴
，
∴=k-k+1=
，
即P点的坐标为（
，）
用-k代k，得点Q的坐标为（
，
）
∴ 
=
=
又A（2，0），B（-1，-1），∴
，
∴ PQ∥AB.
22．（本小题满分14分）
⑴ 
，
若
在
上是单调递减函数，则须
，即
，这样的实数
不存在，
故在上不可能是单调递减函数.
⑵ 若在上是单调递增函数，则≤
，
由于
，故≥3.
从而
⑶ 由⑴、⑵可知在上只能为单调增函数，
若
，则
矛盾，
若
，则
，即
矛盾，
故只有
成立.
⑶的别证：设
，则
，∴
， 
，
两式相减得
∴
，
∵
∴
≥3，又
≤3，∴
∴
，即
，亦即，证毕.