高考数学模拟试卷(五)
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1).若集合M={yy=-2-x},P={yy=![]() },则M∩P= ( )
},则M∩P= ( )
(A).{yy<0} (B).{yy≥1} (C).{yy≥0} (D).
![]()
(2).下列函数中,既是偶函数,又在(0,π)内单调递增的函数是 ( )
(A).y=tanx (B).y=cos(-x)
(C).y=sin(x-![]() ) (D).y=cot
) (D).y=cot![]()
(3).过点A(-2,0)和B(2,3)的直线l的倾斜角为α,则cosα= ( )
(A).![]() (B).
(B).![]() (C).-
(C).-![]() (D).-
(D).-![]()
(4).设等差数列{an}的前n项和为Sn若a1>0, S4=S8,则Sn当取得最大值时,n的值为 ( )
(A).5 (B).6 (C).7 (D).8
(5).已知A、B、C三点在一条直线上,且A(3,-6),B(-5,2),若点C的横坐标为6,
则点C的纵坐标为 ( )
(A).-13 (B).9 (C).-9 (D).13
(6).向量![]() =(1,-2),向量
=(1,-2),向量![]() 与
与![]() 共线,且
共线,且![]() =4
=4![]() ,则
,则![]() = ( )
= ( )
(A).(-4,8) (B).(-4,8)或(4,-8)
(C).(4,-8) (D).(8,4)或(4,8)
(7).设x>-1,则函数y=![]() 的最小值是 ( )
的最小值是 ( )
(A).2![]() (B).2
(B).2![]() +1 (C).2
+1 (C).2![]() -1 (D).以上都不对
-1 (D).以上都不对
(8).下列各组中,M是N的充要条件的是 ( )
(A).M:x+y≤1,N:x2+y2≤1
(B).M:实数a、b,a+b>2,且ab>1,N:a>1且b>1
(C).M:集合E、F和P,P![]() E且P
E且P![]() F,N:P
F,N:P![]() E∩F
E∩F
(D).M:-3≤t≤3![]() ,N:曲线y=
,N:曲线y=![]() (y≠0)与直线y=x+t有公共点
(y≠0)与直线y=x+t有公共点
(9).给出下列命题:
①![]()
②把正方形ABCD平移向量![]() 到A′B′C′D′的轨迹形成的几何体叫做正方体;
到A′B′C′D′的轨迹形成的几何体叫做正方体;
③![]() =“从济南往正比平移3km”,
=“从济南往正比平移3km”,![]() =“从济南向正北平移6km”,则
=“从济南向正北平移6km”,则![]() =2
=2![]() .
.
其中正确的命题是 ( )
(A).①② (B).②③ (C).①②③ (D).①③
(10).某商品的零售价2000年比1999年上涨25%,欲控制2001年比1999年只上涨10%,则2001年应比2000年降价 ( )
(A).15% (B).12% (C).10% (D).5%
(11).已知图①中的图象对应的函数y=f(x),则图②对应的函数在下列给出的四个式子中,只可能是 ( )
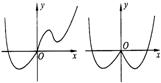 (A).y=f(x) B.y=f(x)
(A).y=f(x) B.y=f(x)
C.y=f(-x) D.y=-f(x)
(12).若0<a<1,函数f(x)=logax,则下列各式中成立的是 ( )
(A).f(2)>f(![]() )>f(
)>f(![]() )
(B).f(
)
(B).f(![]() )>f(2)>f(
)>f(2)>f(![]() )
)
(C).f(![]() )>f(
)>f(![]() )>f(2) (D).f(
)>f(2) (D).f(![]() )>f(2) >f(
)>f(2) >f(![]() )
)
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题.每小题4分;共16分.把答案填在题中横线上.
13.等比数列{an}的前n项和为Sn,若S3=2, S6=6.求a10+a11+a12= .
14.已知x, y 满足x2+2x+y2=0, 则![]() 的最大值是
.
的最大值是
.
15.已知集合A={x2≤x≤π},定义在A上的函数y=logax (a>1)的最大值比最小值大1,则a的值等于 .
16.函数![]() 上是增函数,则实数a的取值范围是
.
上是增函数,则实数a的取值范围是
.

 试卷Ⅱ
试卷Ⅱ
一.选择题(本大题共12小题每小题5分共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二.填空题(本大题共四小题每小题4分共16分)
13. 14. .
15. 16. .
三、解答题:本大题共6小题.共74分.解答应写出文字说明、证明过程或推演步骤.
17. (本小题满分10分)
已知![]()
18.(本小题满分12分)
已知等差数列{an}中,a4+a7+a10=17,a4+a5+a6+…+a14=77.
(1)求{ an}的公差d和a1;
(2)若Sk=64,求k的值.
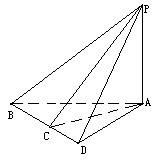
9.如图,已知![]() 面
面![]() ,
,![]() 于D,
于D,![]() .
.
(I)令![]() ,
,![]() ,试把
,试把![]() 表示为
表示为![]() 的函数,并求其最大值;
的函数,并求其最大值;
 (II)在直线PA上是否存在一点Q,使得
(II)在直线PA上是否存在一点Q,使得
![]() ?
?
20.(本小题满分12分)
已知圆C:x2+y2=25及直线l:mx-y-2m+1=0(m∈R).
(1)证明:无论m取什么实数,直线l与圆C恒相交;
(2)求直线l被圆C截得弦长的最小值及此时 的直线方程.
21.(本小题满分12分)
设x , y ∈R,![]() 、
、![]() 为直角坐标系内x、y轴正方向上的单位向量,若
为直角坐标系内x、y轴正方向上的单位向量,若![]() =x
=x![]() +(y+2)
+(y+2)![]() ,
,![]() =x
=x![]() +(y-2)
+(y-2) ![]() 且
且![]() 2+
2+![]() 2=16.
2=16.
(1)求点M(x, y )的轨迹C 的方程;
(2)过定点(0,3)作直线l与曲线C交于A、B两点,设![]() ,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
22.(本小题满分14分)
已知函数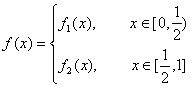
其中![]()
(1)画出y=f(x)的图象;
(2)求y= f(x)的反函数;
(3)设y=g(x)与y= f(x)的图象关于x=-1对称,求y= g(x)的解析式,并写出y= g(x)的单调区间.
高三数学参考答案及评分标准
一、1.D 2.C 3.A 4.B 5.C 6.B 7.C 8.D 9.D 10.B 11.C 12.C
二、13.16 14.11 15.![]() 16.a>-
16.a>-![]()
三、(17).解:![]()
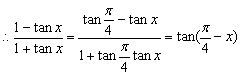
![]()
![]()
(18).解:∵3a7=17, a7= ![]() 11a9=77,
a9=7……………………………………3分
11a9=77,
a9=7……………………………………3分
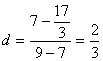 ……………………5分
……………………5分 ![]() …………………6分
…………………6分
(2)![]() …………10分
…………10分
k=12或k=-16(舍去)…………………………………………………………12分
19.
(19)(I)为寻求![]() 与
与![]() 的关系,首先可以将
的关系,首先可以将![]() 转化为
转化为![]() .
.
∵
![]() 面
面![]() ,
,![]() 于D, ∴
于D, ∴
![]() ,
,
∴
![]() ,
,
∴
![]()
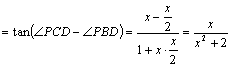 . ∵
. ∵ ![]() 为
为![]() 在面
在面![]() 上的射影,
上的射影,
∴
![]() ,即
,即![]() ,∴
,∴ ![]()
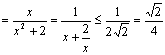 .
.
即![]() 的最大值为
的最大值为![]() ,等号当且仅当
,等号当且仅当![]() 时取得.
时取得.
(II)由正切函数的单调性可知:点Q的存在性等价于:是否存在点Q使得![]()
![]() ,
, ![]() ,
,
令![]()
![]()
![]() ,解得:
,解得:![]() ,与
,与![]() 交集非空,
交集非空,
∴ 满足条件的点Q存在.
(20).(1)证明:将直线方程整理 (x-2)m-y+1=0 ∴直线恒过定点(2,1)…………3分
而此点在圆内,所以直线mx-y-2m+1=0和圆x2+y2=25恒相交………6分
(2)解:当直线l垂直于圆心和点(2,1)连线时截得弦长最短
∴最短弦长=2![]() ……………………8分
……………………8分
此时直线方程为y-1=-2(x-2)…………………………10分
即2x+y-5=0………………………………………………12分
(21).解:(1)由![]() 2+
2+![]() 2=16得x2+y2=4…………………………4分
2=16得x2+y2=4…………………………4分
(2)假设直线l存在,显然l的斜率存在
设A(x1,y1) B(x2, y2)
由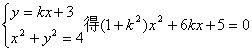 ………………6分
………………6分
![]()
![]()
∴若OAPB为正方形 只有![]() 即x1x2+y1y2=0
即x1x2+y1y2=0
y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9……………………8分
![]() ……10分
……10分
∴存在l且l的方程为y=![]() x+3…………………………12分
x+3…………………………12分
(22).解:(1)f(x)的大致图象如图…………………………4分
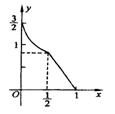 (2)当x∈[0,
(2)当x∈[0,![]() )时 y=2(x-
)时 y=2(x-![]() )2+1
)2+1
即![]() =(x-
=(x-![]() )2
∵x∈[0,
)2
∵x∈[0,![]() ]
]
∴x-![]() =-
=-![]() 即x=
即x=![]() -
-![]()
此时1<y≤![]() ……………………6分
……………………6分
当x∈[![]() ,1]时 y=-2x+2解得x=
,1]时 y=-2x+2解得x=![]() 此时0≤y≤1……………………8分
此时0≤y≤1……………………8分
∴函数f(x)的反函数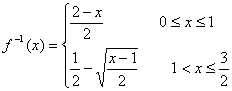 ……………………9分
……………………9分
(3)设函数g(x)图象上任一点(x, y)
由点(x, y )关于x=-1的对称点(-2-x, y)在y=f(x)上………………11分
即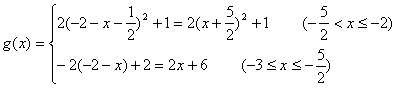
g(x)在[-3,-2]上为单调递增函数…………………………14分