高考数学模拟试卷
本试卷分第一卷（选择题）和第二卷（非选择题）。共150分，考试时间120分钟。
参考公式：三角函数的和差化积公式
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将所选答案填在题后括号内。
１．已知A=｛（x，y）
｝，B=｛（x，y）
｝，则（ ）
A . A
B B .BA C .A
B=
D .Card（AB）= 4
2．若
+）的展开式中各项系数之和为128，则展开式中x2的系数是（ ）
A.189 B. －189 C .252 D .－252
3．若圆
上有且仅有两个点到直线4x－3y－2=0的距离为1，则半径r的取值范围是（ ）
A.（４，6） Ｂ.［４，６） Ｃ.（４，６］ Ｄ.［４，６］
4．先将函数y = f（x）的图象向右平移
个单位，然后再把得到的图象上每一点的横坐标扩大为原来的两倍（纵坐标不变），所得图象恰好与函数f(x)=3sin(x+
)的图象相同，则函数f（x）的解析式为（ ）
A .f(x) =3sin(2x+
) B.
f(x)=3sin(2x+
)
C .f(x) =3sin(2x+
) D. f(x)=3sin(2x
)
5．设正多面体的棱数是E，面数是F，顶点数是V，且每个面都是正n边形，以每个顶点为端点的棱有m条，则以下不正确的是（ ）
A .nF=2E B. mV= 2E C. V+F=E+2 D. mF =2E
6．
0是
的（ ）
Ａ.充分但不必要条件 Ｂ.必要但不充分条件
Ｃ.充分且必要条件 D.不充分也不必要条件
７．映射f：A→B，如果满足集合B中的任意一个元素在Ａ中都有原象，则称为“满射”。已知集合A中有4个元素，集合B中有3个元素，那么从A到B的不同满射的个数为（ ）
A.24 B.6 C. 36 D.72
８．平行六面体中的对角线（包括面对角线、体对角线）交点的个数为（ ）
Ａ.21 Ｂ.15 Ｃ.９ Ｄ.７
９．函数f(x)=x－
在（1，+∞）上是增函数，则实数p的取值范围是（ ）
A.［－1,＋∞
B.［1,+∞
Ｃ. 
－∞,－1］
Ｄ. －∞,1］
10．定义在Ｒ上的非常数函数f(x), 满足：ｆ（ｘ＋２）为偶函数，
且ｆ（１－ｘ）＝ｆ（１＋ｘ）, 则ｆ（ｘ）一定（ ）
Ａ.是偶函数，也是周期函数 Ｂ.是偶函数，但不是周期函数
Ｃ.是奇函数，也是周期函数 Ｄ.是奇函数，但不是周期函数
11．已知a>1，则函数f（x）= log a x的图象与其反函数y=f -1（x）的图象（ ）
A. 不可能有公共点 B. 不可能只有一个公共点
C. 最多只有一个公共点 D. 最多只有两个公共点
12． 从材料工地运送电线杆到500米外的公路，沿公路一侧每隔50米插一根电线杆，又知每次最多只能运3根，要完成运插20根的任务，且送完最后一趟回到材料工地，最佳方案是使运输车运行（ ）
A .14700米 B. 14600米 C. 14000米 D. 13400米
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上。
13．在一个正方体中取四个顶点作为一个四面体的顶点，这样的四面体中，直角三角形最多有
个。
14．利用简单随机抽样从含有12个个体的总体中抽取一个容量为4的样本，则总体中每个个体被抽到的概率为 。
15．设
若函数f（x）=
，则f（x）的定义域为
16．若对于任意a
[-1,1], 函数f(x) = x
+ (a－4)x + 4－2a的值恒大于零, 则x的取值范围是
。
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算
17．（本小题满分12分）
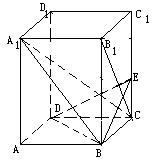
如图，在长方体ABCD－A1B1C1D1中，AB=BC=3，BB1= 4， BE
B1C交CC1于E。
（1）
求证：直线 A1C直线BE；
（2） 求直线A1B与平面BDE所成角的余弦值。
18．（本小题满分12分）
已知数列{an}的前n项和为Sn，且对任意正自然数n，总有Sn=p(an-1)(p为常数且p≠0, p≠1)，数列{bn}中，
bn=2n+q(q为常数)。
（1）求数列{an}的通项公式；
（2）若a1=b1 ,a2>b2 ,求常数p的取值范围。
19．（本小题满分12分）
已知F1、F2分别是椭圆
的左、右焦点，P是该椭圆上的一点，且满足
·
=2，求△PF1F2的面积。
20．（本小题满分12分）
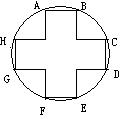
有一种变压器铁芯的截面呈如图所示的正十字形，
为保证所需的磁通量，要求正十字形的面积为
４
ｃｍ２，为了使用来绕铁芯的铜线最省，
即正十字形外接圆周长最短，应如何设计
正十字形的长（如ＤＧ），和宽（如ＡＢ）？
21.（本小题满分12分）
某啤酒厂生产两种啤酒，其中1０.５°啤酒x桶，12°啤酒y桶。粮食、啤酒花和麦芽是三种有约束的资源，每天分别提供480斤、160两和1195斤。假设生产一桶1０.５°啤酒需要粮食5斤，啤酒花4两，麦芽20斤；生产一桶12°啤酒需要粮食15斤，啤酒花4两，麦芽35斤。售出每桶10.5°啤酒可获利13元，每桶12°啤酒可获利23元。问x 、y等于多少时，工厂的利润最大, 最大利润是多少？
22．（本小题满分14分）
设函数
，其中0<
<
。
（1）若
在x=s及x=t处取得极值，其中s<t，求证：
<s<<t<；
（2）若过原点且与曲线y=相切的两条直线互相垂直，试求点M（，）的轨迹方程。
参考答案
1 D 2 B 3 A 4 B 5 D 6 B 7 C 8 B 9 A 10 A 11 D 12 C
13
4 14 
15 （
16 （
17 （1）∵ABCD－A1B1C1D1是长方体，∴A1B1⊥平面B1BCC1，且B1C是A1C在平面B1BCC1上的射影，∵BE⊥B1C，∴由三垂线定理得A1C⊥BE。……………………………………4/
（２）连结AC,∵A1A平面ABCD，AC是A1C在平面ABCD上的射影，又ABCD是正方形，∴AC⊥BD，由三垂线定理得A1C⊥BD。
∴A1C⊥平面BDE。……………………………………………………………………………7/
设A1C平面BDE=O，连BO，则∠A1BO是直线A1B与平面BDE所成的角。……………9/
∵AB=BC=3，BB1=4，∴AC1=
，在Rt△A1BC中，BO=
，
∴cos∠A1BO=
。…………………………………………………………………………12/
18（1）当n=1时，a1=
s1= p（a1－1），∵p≠1，∴a1=
。……………………………2/
当n≥2时，an = sn－sn－1= p（an－1）－p（an－1－1）= p an－p an－1，
∵p≠1，∴an= an－1 ，
∵p≠0，a1≠0，∴an－1≠0 ，故
，∴{ an}是首项a1=，公比q= 的等比数列，∴an=（
。…………………………………………………………………7/
（2）由条件有2+q=，且4+q<
，消去q，得2+<，解得
<p<1或1<p<2，故所求常数p的取值范围为（，1）
（1，2）。……………………12/
19 ∵a2=4，b2=3，∴a=2 ,c=1.设∠F1PF2=
，则
，在△F1PF2中，由余弦定理有
，∴
，
得
。………………………………………………………………………５／
又∵
，∴
。……………………８／故
。…………………………………………………10/
三角形F1PF2的面积S=
。…………………………………………12/
20 设外接圆半径为R，AB =x（0<x<R），DG =y，则4R2=x2+y2
（1），有条件有2xy－x2=4，∴y=
（2），代入（1）得4R2= x2 +
。………………………５／
∴4R2=
=10+
。……………………………７/
当且仅当
，即x=2时，等号成立。………………………………………………9/
代入（2）得y=1+，∴当 x=2 且y=1+时，4R2有最小值，此时正十字形外接圆周长最短。……………………………………………………………………………………………11/
答：正十字形的长和宽分别为(1+)cm和2cm时，用来绕铁芯的铜线最省。………12/
5x+15y≤480
4x+4y≤160
21由条件有 20x+35y≤1195…………………………………………………………………5/
x≥0
y≥0
目标函数为：z = 13x + 23y…………………………………………………………………7/
画出可行域D，由图可知z = 13x + 23y在直线5x+15y=480和直线20x+35y=1195的交点
P（9，29）上达到最大值，即当x=9且y=29时，z取得最大值，最大值为784。
答：当生产9桶1０.５°啤酒、29桶12°啤酒时，工厂的利润最大，最大利润为784元。………………………………………………………………………………………………12/
22 （1）∵
∴
。……………2/
由条件可知s、t是方程=0的根。
，
∵0<<，∴
>0，
<0，
>0，∵s<t，∴ <s<<t<。……………6/
（2）设函数f(x)的图象为C，则曲线C过原点的切线l1的斜率k1=
。………8/
设P（m，n）（m
0）是曲线C上的一点，则曲线C过点P的切线l2的方程为
。……………………………………………………10/
设该切线过原点，则
， （1）
∵P（m，n）在曲线C上，∴
，代入（1）得
=
，解得m=
。…………………12/
故l2的斜率k2=
，∵l1⊥l2，∴
，即
（0<<），此即为所求点M的轨迹方程。……14/