第一学期期末统一考试高三数学（理科）试卷
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页。第Ⅱ卷3至8页。共150分。考试时间120分钟。
第Ⅰ卷（选择题50分）
参考公式：
三角函数的和差化积公式
正棱台、圆台的侧面积公式
其中c’、c分别表示上、下底面周长，l表示斜高或母线长台体的体积公式
其中S’、S分别表示上、下底面面积，h表示高
一、选择题：本题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的，请把你认为正确的选项前的字母填在题后的括号内。
（1）设集合
，若
，则a的取值范围是（ ）
（A）
（B）
（C）
（D）
（2）已知二面角
，直线
，
，且a与l不垂直，b与l不垂直，那么（ ）
（A）a与b可能垂直，但不可能平行 （B）a与b可能垂直，也可能平行
（C）a与b不可能垂直，但可能平行 （D）a与b不可能垂直，也不可能平行
（3）函数
在一个周期内的图象如图所示，函数
解析式为（ ）
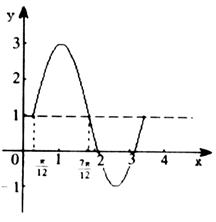
（A）
（B）
（C）
（D）
（4）双曲线c：
的左、右焦点分别为
，过焦点
且垂直于x轴的弦O ，
，则双曲线c的离心率为（ ）
（A）
（B）
（C）
（D）
（5）如图，O为直二面角
的棱MN上的一点，射线OE，OF分别在
内，且∠EON=∠FON=45°，则∠EOF的大小为（ ）
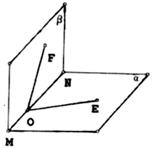
（A）30° （B）45° （C）60° （D）90°
（6）在等差数列
中， 
，公差d<0，前n项和是
，则有（ ）
（A）
（B）
（C）
（D）
（7）用不着，2，3，4这5个数字组成无重复数字的五位数中，若按从小到大的顺序排列，那么12340应是（ ）
（A）第9个数 （B）第10个数 （C）第11个数 （D）第12个数
（8）下列四个命题：
①满足
的复数只有
；
②若a，b是两个相等的实数，则
是纯虚数；
③复
的充要条件是
；
④复平面内x轴即实轴，y轴即虚轴。
其中正确的有（ ）
（A）1个 （B）2个 （C）3个 （D）4个
（9）在
中，
，是A>B的（ ）
（A）充分而不必要条件 （B）必要而不充分条件
（C）充要条件 （D）即不充分也不必要条件
（10）过抛物线
的焦点作直线与此抛物线交于P，Q两点，那么线段PQ中点的轨迹方程是（ ）
（A）
（B）
（C）
（D）
第Ⅱ卷（非选择题共100分）
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
（11）已知
，则
=________________。
（12）在一个棱长为
的正四面体内有一点P，它到三个面的距离分别是1cm，2cm，3cm，则它到第四个面的距离为_______________cm。
（13）设等比数列
的前n项和为，前n+1项的和为
，则
=___________________。
（14）抛物线
和圆
上最近两点的距离是_________________。
三、解答题：本大题共6小题，共84分。解答应写出文字说明，证明过程或演算步骤。
（15）（本小题满分14分）
解关于x的不等式
（Ⅰ）
；
（Ⅱ）
，其中
。
（16）（本小题满分14分）
已知：定义在R上的函数为奇函数，且在
上是增函数。
（Ⅰ）求证：在
上也是增函数；
（Ⅱ）对任意
，求实数m，使不等式
恒成立。
（17）（本小题满分14分）
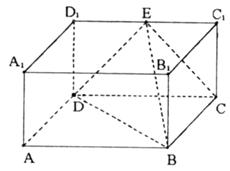
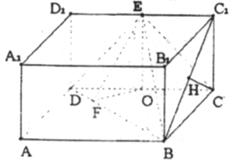
在长方体ABCD—
中，AB=2，
，E为
的中点，连结ED，EC，EB和DB。
（Ⅰ）求证：平面EDB⊥平面EBC；
（Ⅱ）求二面角E-DB-C的正切值；
（Ⅲ）求异面直线EB和DC的距离。
（18）（本小题满分14分）
某造纸厂拟建一座平面图形为矩形且面积为200平方米的二级污水处理池（平面图如图所示），池的深度一定，池的外圈周壁建造单价为每米400元，中间一条隔壁建造单价为每米100元，池底建造单价每平方米60元（池壁厚度忽略不计）。
（Ⅰ）污水处理池的长设计为多少米时，可使总造价最低；
（Ⅱ）如果受地形限制，污水处理池的长、宽都不能超过14.5米，那么此时污水处理池的长设计为多少米时，可使总造价最低。
（19）（本小题满分14分）
P为椭圆c：
上除
，
的两点外的一点。
（Ⅰ）求直线
P与
的斜率的乘积；
（Ⅱ）设P（x，y），求证：
；
（Ⅲ）设
，求证：
。
（20）（本小题满分14分）
已知函数
，满足条件：
①
；②
；③
；
④当x>y时，有
。
（Ⅰ）求f(1)，f(3)的值；
（Ⅱ）由f(1)，f(2)，f(3)的值，猜想f(n)的解析式；
（Ⅲ）证明你猜想的f(n)的解析式的正确性。
高三期末试卷
数学（理工农医类）参考答案及评分标准 2004.1
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | B | D | C | C | A | B | A | C | D |
二、填空题
11.
12.4
13.
14.
三、解答题
15.解：（Ⅰ）
，
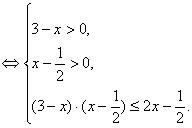…………………………………………4分
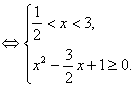……………………………………………………6分
∵
，……………………………………7分
∴原不等式的解集为
。……………………………………8分
（Ⅱ）
，等价于
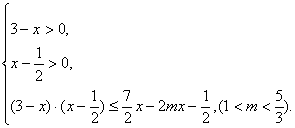
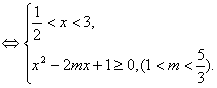
。………………………………10分
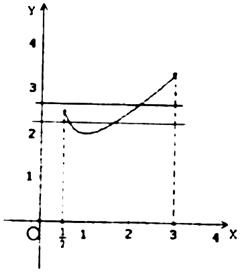
令直线
，曲线
，作出直线l与曲线c的图象。
（1）当
，即
时，直线l与曲线c有两个公共点，公共点的横坐标是
，此时不等式的解集为
。……………………………………12分
（2）当
，即
时，直线l与曲线c有一个公共点，公共点的横坐标是
，此时不等式的解集为
。…………14分
16.（Ⅰ）证明：设
，且
，则
，且
。
…………………………2分
∵在上是增函数，
∴
…………………………………………………………4分
又为奇函数，∴
……………………………………6分
∴
。
∴在上也是增函数。…………………………………………8分
（Ⅱ）∵函数在和上是增函数，且在R上是奇函数
∵在
上是增函数。…………………………………………10分
∵，
∴
。
，
，………………………………………………12分
，
。
∵当
时，
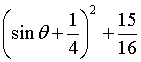的最大值为
，
∴当
时，不等式恒成立。…………………………………………14分
17.（Ⅰ）证明：在长方体ABCD-中，AB=2，，E为的中点。
∴
为等腰直角三角形，
。
同理
。
∴
，即DE⊥EC。……………………………………………2分
在长方体ABCD-中，BC⊥平面
，又DE
平面，
∴BC⊥DE。……………………………………………………………………4分
又
，
∴DE⊥平面EBC。
∵平面DEB过DE，
∵平面DEB⊥平面EBC。……………………………………………………5分
（Ⅱ）解：如图，过E胡平面中作EO⊥DC于O。
在长方体ABCD-中，
∵面ABCD⊥面，
∴EO⊥面ABCD。
过O在平面DBC中作OF⊥DB于F，连结EF
∴EF⊥BD。
∠EFO为二面角E-DB-C的平面角。………………………………7分
利用平几知识可得
。…………………………10分
（Ⅲ）解：E在上，B在AB上，在长方体ABCD-中，
，
∴EB在平面
内。
又∵DC//AB
∴DC//平面。
直线DC到平面的距离就等于异面直线DC和EB的距离。………………12分
在长方体ABCD-中，平面⊥平面
，连结
，在平面
中，过C作
。
CH⊥平面，CH为所求的距离。
∴
。…………………………………………………………14分
18.（Ⅰ）解：设污水处理池的长为x米，则宽为
米。………………………2分
总造价
。…………………4分
=36000（元）………………………………………………………………6分
当且仅当
时，即x=15等号成立。
答：当污水处理池的长为15米（宽为
米）时，总造价最低。………………8分
（Ⅱ）解：依（Ⅰ）有总造价
，当且 当x=15等号成立，
，从而考虑条件：
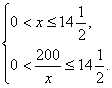
即
，在
上的单调性。……………………10分
设
，且。
由于
。………………………………12分
∵，且
，
∴
。
∴
。
∴
。
∴在
上单调递减。
∴
。
∴当长为
米时总造价最低。…………………………………………14分
19.（Ⅰ）解：设点P（x，y），则有
，………………………………………………2分
由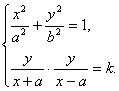
变形为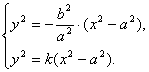
…………………………………………4分
∴
。即
。……………………………………5分
（Ⅱ）证明：（1）当点P在x轴的上方时，y>0。
，
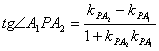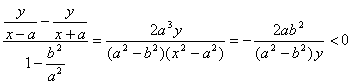。…………7分
（2）当点P在x轴的下方时，y<0，同理可得
。
∴
是钝角，
…………………………10分
（Ⅲ）证明：由三角形的面积公式得
。………………12分
。
∴
。
得
∴
。……………………………………………………14分
20.（Ⅰ）解：∵
，又，
∴
。…………………………………………………………………………2分
又∵
，…………………………………………4分
，且
。
∴
。…………………………………………………………………………5分
（Ⅱ）解：由
猜想
。…………8分
（Ⅲ）用数学归纳法证明：
（1）当n=1时，f(1)=1，函数解析式成立；
（2）假设
时，
，函数解析式成立；
①若
，
。………………10分
②若
，
，
。
∴
。……………………………………12分
即
时，函数解析式成立。
综合（1）（2）可知，成立。……………………14分