第一学期期末质量抽测高三数学试卷
班级 学号 姓名 成绩
一、填充题（每小题4分，共48分）
1. 
___________.
2. 若集合A={xx＜3},B={xx≥a},且A∩B=Æ,则实数a的取值范围是__________.
3. 函数
的图象经过点(1,3),其反函数的图象过点(2,0),则
的表达式为=___________.
4. 袋内有大小相同的四个白球和三个黑球,从中任意摸出3个球,则其中只有一个黑球的概率是_____.
5．若
为虚数,且
,则=________.
6．若tg(a+b)=
,tg(b+
)=
,则tg(a-)=_______.
7．设I是全集，非空集合P、Q满足PÌQÌI .若含P、Q、I的一个集合运算表达式，使运算结果为F，则这个运算式可以是 （只要写出一个表达式）.
8．[理]过极点且圆心在(3,p)的圆的极坐标方程是________________________.
[文]某工程由下列工序组成,则该工种的总时数为________,
| 工 序 | a | b | c | d | e | f |
| 紧前工序 | - | a | a | b | c | d,e |
| 工时数(天) | 3 | 3 | 2 | 4 | 7 | 5 |
9．函数
的最小值为_______.
10.若函数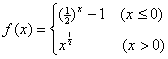
,则使
＞１的
的取值范围是___________.
11.设
是
(n=2,3,4,…)展开式中
的系数,则
_______.
12.若
,我们把使乘积
为整数的数
叫做“劣数”,则在区间(1,2002)内所有劣数的和为_______.
二、选择题（每小题4分，共16分）
13．“
”是“
”成立的 （ ）
（A）充分非必要条件（B）必要非充分条件（C）充要条件（D）既非充分也非必要条件
14．已知A={yy=x,xÎR},B={yy=x2,xÎR}，则A∩B等于 （ ）
（A）{(0,0),(1,1)} （B）{xxÎR} （C）{yy≥0} （D）Æ
15．[理]曲线的参数方程为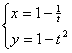
(t为参数,t≠0),则它的普通方程是 （ ）
（A）(x-1)2(y-1)=1（B）
（C）
（D）
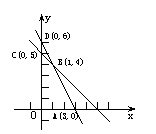[文]满足不等式组
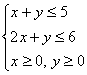的点中,使目标函数
k=3x+4y取得最大值的点的坐标是 （ ）
（A）(3,0) （B）(1,4) （C）(0,5) （D）(0,6)
16．足球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分,那么一个队打14
场共得19分的情况共有 （ ）
（A）3种 （B）4种 （C）5种 （D）6种
三、解答题(12¢+12¢+14¢+14¢+16¢+18¢)
17．已知f(x)是定义在(-3,3)上的奇函数,且在[0,3)上的解析式为y=(x-1)2-1.
(1)求f(x)在(-3,0)上的解析式；
(2)
在坐标系中作出函数f(x)的图象，并写出其值域.
18．已知不等式x2-ax-2a2＜0(aÎR).
(1)解此不等式；
(2)若x=1在不等式的解中,求a的取值范围.
19．已知模为1的两个复数
、
在复平面上对应的点均第一象限内,若2=(-1+
)
,
(1)求； (2)若=
,求+.
20．设{an}是等比数列,若bn=an+1-an(nÎN),且数列{bn}的前n项和Sn=
.
(1)求数列{an}的首项a1和公比q； （2）求
(b1+b3+…+b2n-1)
21．某港口水的深度y(米)是时间t(单位:时)的函数,其中0≤t＜24,t=0时为零点.下面是
该港口某一天的水深表:
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 |
| y(米) | 10 | 12.8 | 9.8 | 7.1 | 10.2 | 13.2 | 10 | 6.9 |
经过常期统计,描出的曲线如图所示,经拟合,该曲线可近似地看作函数y=Asinωt+B(A＞0)的图象.
(1)根据数据和曲线(为方便起见,可将小数四舍五入到整数),求出y=f(t)的解析式；
(2)在一般情况下,船底距海底4.5或4.5米以上时能安全行驶,若某船的吃水深度(船底与水面距离)为7米,那么该船在什么时间能够安全进港?
(3)
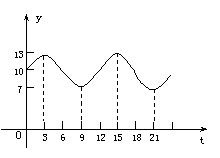若该船必须在当天安全进港和离港,由(2)的计算,它在港内停留的时间最长能有多少小时?(忽略进离港所花有时间).
22．设函数f(x)=
-ax(a＞0).
(1)当a≥1时,求证f(x)在区间[0,+∞)上是减函数；
(2)当0＜a≤1时，解方程f(x)=1；
(3)当0＜a＜1时，判断f(x)在区间[0，+∞)上是否为单调函数,说明理由.