第一学期期末质量监控试数学卷
高 三 数 学 (A卷)
(考试时间120分钟,满分150分)
一、填空题(每小题4分,共48分)
1.方程![]() 的解是
的解是 ![]() 。
。
2.设![]() 是
是![]() 的反函数,则
的反函数,则![]()
![]() 。
。
3.设![]() ,则
,则![]()
![]() 。
。
4.经过同类项合并![]() 的展开式中
的展开式中![]() 的系数为
的系数为![]() ,则
,则![]()
![]() 。
。
5.设函数![]() ,则
,则![]() 的值为
的值为 ![]() 。
。
6.![]()
![]() 。
。
7.六位身高全不相同的同学拍照留念,摄影师要求前后两排各三人,则后排每人均比前排同学高的概率是 ![]() 。
。
8.方程![]() 在区间
在区间![]() 上所有解的和是
上所有解的和是 ![]() 。
。
9.设![]() ,且
,且![]() 恒成立,则
恒成立,则![]() 的最大值为
的最大值为 ![]() 。
。
10.在![]() 中,已知
中,已知![]() ,则
,则![]() 的面积为
的面积为 ![]() 。
。
11.写出直线![]() 与直线
与直线![]() 互相垂直的一个充分不必要条件
互相垂直的一个充分不必要条件 ![]() 。
。
12.若![]() 是等差数列,则
是等差数列,则![]() ,则类似的结论有
,则类似的结论有![]()
![]() (答案不唯一)。
(答案不唯一)。
二、选择题(每小题4分,共16分)
13.设函数![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,记
,记![]() ,则数列
,则数列![]() ( A )
( A )
A.是公差不为零的等差数列 B.是公比不为1的等比数列
C.是常数数列 D.不是等差数列也不是等比数列
14.一位老师让两位学生计算数![]() 的算术平均数,学生甲这样求:先求x与y的平均数,再求这个平均值与z的平均值,学生乙的算法是:先求
的算术平均数,学生甲这样求:先求x与y的平均数,再求这个平均值与z的平均值,学生乙的算法是:先求![]() 的和,再求这个和除以3的商,如果学生甲和乙求出的数据分别为S和T,且
的和,再求这个和除以3的商,如果学生甲和乙求出的数据分别为S和T,且![]() ,则S和T的大小关系是
( B )
,则S和T的大小关系是
( B )
![]() A.
A.![]() B.
B.![]() C.
D.不确定
C.
D.不确定
15.下面给出的每一组数分别表示三条线段的长,将每组数表示的三条线段首尾相连,其中恰能构成三角形的是 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
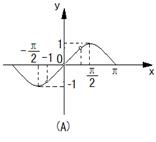
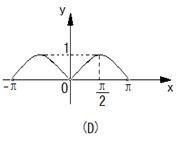
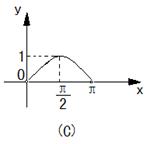
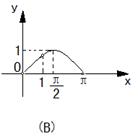 16.函数
16.函数![]() 在区间
在区间![]() 上的图象是
( B )
上的图象是
( B )
三、解答题(本大题共86分)本大题6题
17.(本题12分)已知集合![]() ,求:①
,求:①![]() ;(6分)②
;(6分)②![]() .(6分)
.(6分)
![]()
![]()
![]()
18.(本题12分)已知函数![]() ,满足
,满足![]() ,设
,设![]() 、
、![]() ,且
,且![]() 、
、![]() 两点在函数
两点在函数![]() 的图象上,若
的图象上,若![]() 、
、![]() 两点关于直线
两点关于直线![]() 对称,求直线
对称,求直线![]() 的方程。
的方程。
![]()
![]() 的方程:
的方程:![]()
19.(本题12分)已知函数![]()
①求a、b的值及![]() 的最大值和周期;(6分)
的最大值和周期;(6分)
②若![]() 且
且![]() 是方程
是方程![]() 的两根,求
的两根,求![]() 的值。(6分)
的值。(6分)
![]() ,
,![]() 的最大值为
的最大值为![]() ,
,![]()
![]()
20.(本题14分)
已知复数![]() 为纯虚数
为纯虚数
(1)用a来表示复数![]() ;(7分)
;(7分)
(2)设集合![]()
![]() 是否存在实数a、b使 ①
是否存在实数a、b使 ①![]()
②![]() 同时存在?若存在,求出
同时存在?若存在,求出![]() ,若不存在,请说明理由。(7分)
,若不存在,请说明理由。(7分)
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
21.(本题18分)2003年元月某市人民政府下达了停止办理摩托车入户手续文件,2002年底该市区居民摩托车拥有量达32万辆,据统计每7辆摩托车排放的有害污染物总量相当于一辆公交车排放的污染物,而每辆摩托车的运送能力是一辆公交车运送能力的8%。
假设从2003年起几年内,某市决定退役部分摩托车,第一年退役a万辆,以后每年是上年75%,同时增加公交车的数量,使新增公交车的运送的能力总量等于退役的摩托车原有的运送能力的总量。
①摩托车全部退役后,同时增加相应公交车后,全市空气中排放污染物减少了百分之几?(6分)
②求增加公交车的数量y(万辆)与时间n (年)之间的函数关系式(不必求定义域)(6分)
③若经过5年,剩余的摩托车与新增公交车的排放污染物的总量不超过32万辆摩托车排放污染物总量的60%,求第一年至少退役摩托车多少万辆?(6分)
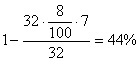
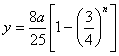
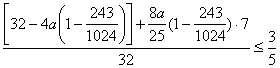 ,
,![]()
![]() (万辆)
(万辆)
22.(本题18分)递增数列1,2,3,4,5,6……由一些正整数组成,它们或者是2的幂,或者是由2个不同的幂之和(比如![]() ),把它们按小到大排列成数列
),把它们按小到大排列成数列![]() ,将
,将![]() 各项按照上小下大,左小右大的原则,写成如下三角形数表
各项按照上小下大,左小右大的原则,写成如下三角形数表
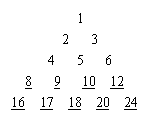 ①写出这个三角数表的第四行与第五行;(4分)
①写出这个三角数表的第四行与第五行;(4分)
②设三角形数表每行左边第一个数为一列,记作![]() ,写出
,写出![]() 的通项公式,并求出
的通项公式,并求出![]() 的值,指出对应于
的值,指出对应于![]() 的第几项?(4分)
的第几项?(4分)
![]()
③求![]() ;(5分)
;(5分)![]() (第14行的第9个数)
(第14行的第9个数)
④请说明三角形数表中右边第一列是什么数列?(5分)![]()