第一学期期中考试高三数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3至8页。共150分。考试用时120分钟。
第Ⅰ卷(选择题,共60分)
注意事项:1.答卷前,将自己的班级、姓名、学号填在试卷指定的位置上.
2.每小题选出答案后,填在答题卡指定的位置上.
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1).![]()
A.1 B.-1 C.![]() D.
D.![]()
(2).已知集合![]() ,若
,若![]() ,则实数
,则实数![]() 的值是
的值是
A.0 B.1 C.-1 D.1或-1
(3).已知![]() ,且
,且![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(4).函数![]() 在区间
在区间![]() 上是
上是
A.增函数,且![]() B.增函数,且
B.增函数,且![]()
C.减函数,且![]() D.减函数,且
D.减函数,且![]()
(5).已知函数![]() 是偶函数,当
是偶函数,当![]() 时,
时,![]() ,则当
,则当![]() 时 ,
时 ,![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(6).数列![]() 满足条件
满足条件![]() ,则该数列是
,则该数列是
A.等差数列 B.等比数列
C.从第二项起是等差数列 D.从第二项起是等比数列
(7). 已知![]() 是可导的偶函数,且
是可导的偶函数,且![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(8).设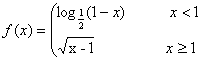 ,若
,若![]() ,则
,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(9).已知数列![]() 成等差数列,
成等差数列,![]() 成等比数列,则
成等比数列,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() 或
或 ![]() D.
D.![]()
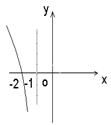
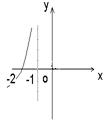
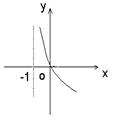
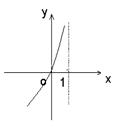 (10).已知
(10).已知![]() ,则
,则![]() 的图象是
的图象是
A. B. C. D.
(11).若数列![]() 的前
的前![]() 项和
项和![]() ,则
,则![]() 的值为
的值为
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
(12).已知方程![]() 有一根的范围是(2,4),则实数
有一根的范围是(2,4),则实数![]() 的值是
的值是
A. ![]() B.
B. ![]() C.
C. 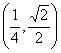 D.
D. ![]()
第Ⅱ卷(非选择题,共90分)
二.填空题: 本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13).若等差数列![]() 中,
中,![]() ,则
,则![]() .
.
(14).若![]() ,则
,则![]() .
.
(15).有6名学生借助互连网学习,每个学生上网的概率都是0.5(相互独立),设同时上网的人数为![]() .
.![]() =
;
=
;![]() = .
= .
(16).已知定义在R上的偶函数![]() 满足
满足![]() ,且在区间[-1,0]上是增函数,给出下面关于
,且在区间[-1,0]上是增函数,给出下面关于![]() 的命题:①
的命题:①![]() 是周期函数;②
是周期函数;②![]() 在[1,2]上是减函数;③
在[1,2]上是减函数;③![]() 的图象关于
的图象关于![]() 对称;④若
对称;④若![]() 的反函数为
的反函数为![]() ,则
,则![]() 的反函数为
的反函数为![]() .其中真命题的序号是
.
.其中真命题的序号是
.
三.解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知![]() .
.
(Ⅰ)求![]() 的定义域,判断其奇偶性;
的定义域,判断其奇偶性;
(Ⅱ)判断![]() 在定义域上的单调性,并证明之.
在定义域上的单调性,并证明之.
(18)(本小题满分12分)
数列![]() 中,
中,![]() ,数列
,数列![]() 中,
中,![]() .
.
(Ⅰ)求数列![]() 通项公式;
通项公式;
(Ⅱ)求数列![]() 通项公式与前
通项公式与前![]() 项的和.
项的和.
(19)(本小题满分12分)
设![]() .
.
![]() :函数
:函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
![]() :不等式
:不等式![]() 的解集为R;
的解集为R;
如果![]() 和
和![]() 有且只有一个是真命题,求实数
有且只有一个是真命题,求实数![]() 的取值范围.
的取值范围.
(20)(本小题满分12分).
已知函数![]() 是定义在R上的奇函数.
是定义在R上的奇函数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的反函数
的反函数![]() 及其定义域;
及其定义域;
(Ⅲ)解关于![]() 的不等式
的不等式![]() .
.
(21) (本小题满分12分)
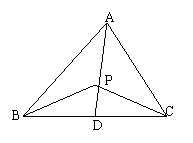
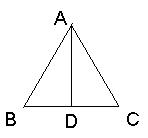 已知有三个镇分别位于A、B、C三地,若AB=AC,AD⊥BC,D为垂足,AD相距
已知有三个镇分别位于A、B、C三地,若AB=AC,AD⊥BC,D为垂足,AD相距![]() km ,BC相距4km.现要在BC的垂直平分线上选一点P建一个变电站.
km ,BC相距4km.现要在BC的垂直平分线上选一点P建一个变电站.
(Ⅰ)若![]() ,点P距各镇多远时,才能使送变电线路最短;
,点P距各镇多远时,才能使送变电线路最短;
(Ⅱ)要使点P到三镇的最远距离为最小,点P应位于何处?
(22) (本小题满分14分)
设![]() 为函数
为函数![]() 展开式中
展开式中![]() 的系数.
的系数.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)证明对任意![]() ,
,![]() ;
;
(Ⅲ)求![]()
第一学期期中考试
高三数学答案
一、选择题:B C D B D D B C A C B C
二、![]()
![]()
![]() 填空题:13、-60 14、 3 15、
填空题:13、-60 14、 3 15、![]() ,3 16、①③④
,3 16、①③④
三、![]() 解答题:
解答题:
17、解:(1)∵![]() >0且x≠0 即
>0且x≠0 即![]() <0且x≠0∴-1<x<0或0<x<1
<0且x≠0∴-1<x<0或0<x<1
∴定义域为(-1,0)∪(0,1)
∵又f(-x)=![]() +ln
+ln![]() ∴f(x)+f(-x)=ln1=0 即f(x)是奇函数.
∴f(x)+f(-x)=ln1=0 即f(x)是奇函数.
(2)设x1,x2∈(0,1),且x1<x2,则
f(x1)-f(x2)= ![]() +ln
+ln![]() +
+![]() -ln
-ln![]() =
=![]() +ln
+ln![]()
∵0<x1<x2<1∴x1-x2<0,x1x2>0,0<1+x1<1+x2,0<1-x2<1-x1,∴0<![]() <1,0<
<1,0<![]() <1∴0<
<1∴0<![]() <1即ln
<1即ln![]() <0 ∴f(x1)-f(x2)<0∴f(x1)<f(x2)
<0 ∴f(x1)-f(x2)<0∴f(x1)<f(x2)
∴f(x)在(0,1)上是增函数,又∵f(x)是奇函数∴f(x)在(-1,0)上也是增函数
18、解:(1)∵a1=3,an+1-2an=0∴{an}是首项为3,公比为2的等比数列∴an=3•2n-1
(2)∵bn•an=(-1)n ∴bn=(-1)n•![]() =(-1)n•
=(-1)n•![]()
∴Sn=b1+b2+…+bn=-![]() +
+![]() +…+(-1)n
+…+(-1)n![]() =
=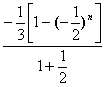
=-![]() =
=![]()
19、如果P是真命题,则a2-a-1>1∴a2-a-2>0∴a<-1或a>2又∵a>0∴a>2
如果q是真命题,则Δ=(a-1)2-4<0∴-1<a<3又∵a>0∴0<a<3
∵P与q中有且只有一个真命题,∴0<a≤2或a≥3 故a∈(0,2)∪[3,+∞]
20、解:(1)∵f(x)在R上有定义,且f(x)是奇函数∴f(0)=0∴a-1=0即a=1
(2)∵y=1-![]() ∴2x+1=
∴2x+1=![]() ∴2x=
∴2x=![]() ∴x=log2
∴x=log2![]()
∴y=f-1(x)= log2![]() (-1<x<1)
(-1<x<1)
(3)∵f-1(x)<1∴log2![]() <1∴
<1∴![]() >0且
>0且![]() <2解得-1<x<
<2解得-1<x<![]()
 ∴不等式f-1(x)<1的解集是(-1,
∴不等式f-1(x)<1的解集是(-1, ![]() )
)
21、解:(1)如图,设PD=xkm,供电线路总长为ykm,则
y=2![]() (0≤x≤6)∴y,=
(0≤x≤6)∴y,=![]()
![]() 令y,=0得2x=
令y,=0得2x=![]() ,∴x=
,∴x=![]() ∴当点P距A地6-
∴当点P距A地6-![]() km,距B、C两地都是
km,距B、C两地都是![]() km时,供电线路最短。
km时,供电线路最短。
![]() ,
, ![]() ≥a-x
≥a-x
(2)点P到三镇的最远距离为f(x)=
a-x. ![]() <a-x
<a-x
由![]() ≥a-x得2ax≥a2-4即x≥
≥a-x得2ax≥a2-4即x≥![]() ,∴当a≥2时,
,∴当a≥2时,![]()
在(![]() ,+∞)是增函数,a-x在(0,
,+∞)是增函数,a-x在(0, ![]() )上是减函数,∴当x=
)上是减函数,∴当x=![]() 时,f(x)取最小值,此时P在D上方
时,f(x)取最小值,此时P在D上方![]() km处,又∵当0<a<2时,
km处,又∵当0<a<2时,![]() 在x=0处取最小值2,而a-x在(-∞,
在x=0处取最小值2,而a-x在(-∞, ![]() )上是减函数,其最小值a-x>2此时点P与D重合。
)上是减函数,其最小值a-x>2此时点P与D重合。
22、解:(1)∵f2(x)=(1+2x)(1+22x)∴展开式中x2的系数为2•22∴a2=2•22=8
同理f3(x)=(1+2x)(1+22x)(1+23x),∴展开式中x2的系数为2•22+(2+22)23
∴a3=2•22+(2+22)23=56
(2)①当n=2时,左=a2=8,右=![]() (22-1)(2-1)=8,∴左=右,即等式成立。
(22-1)(2-1)=8,∴左=右,即等式成立。
②假设当n=k(k≥2)时,等式成立,即ak=![]() (2k-1)(2k-1-1),
(2k-1)(2k-1-1),
∴ak+1=ak+(2+22+…+2k)•2k+1=![]() (2k-1)(2k-1-1)+
(2k-1)(2k-1-1)+![]()
= ![]() (2k-1)(2k-1+
(2k-1)(2k-1+![]() •2k+2)=
•2k+2)= ![]() (2k-1)(4•2k-1-1)=
(2k-1)(4•2k-1-1)=
![]() (2k+1-1)(2k-1)
(2k+1-1)(2k-1)
∴当n=k+1时等式成立,由①②可知对一切大于等2的正整数,等式均成立。
(3)∵an=![]() (2n-1)(2n-1-1)∴
(2n-1)(2n-1-1)∴![]()
∴![]() =
=![]() =
=![]()
∴![]()
![]() =
=![]()
![]() =
=![]()