|
|
学科：数学 |
| 教学内容：第八章 多面体和旋转体 |
一、考纲要求
1.理解棱柱、棱锥、棱台、圆柱、圆台、球及其有关概念和性质.
2.掌握直棱柱、正棱锥、正棱台和圆柱、圆锥、圆台、球的表面积和体积公式(球缺体积公式不要求记住)，并能运用这些公式进行计算.
3.了解多面体和旋转体的概念，能正确画出直棱柱、正棱住、正棱台、圆柱、圆锥、圆台的 直观图.
4.对于截面问题，只要求会解决与几种特殊的截面(棱柱、棱锥、棱台的对角面，棱柱的直截面，圆柱、圆锥、圆台的轴截面和平行于底面的截面，球的截面)以及已给出图形或它的全部顶点的其他截面的有关问题.
二、知识结构
1.几种常凸多面体间的关系
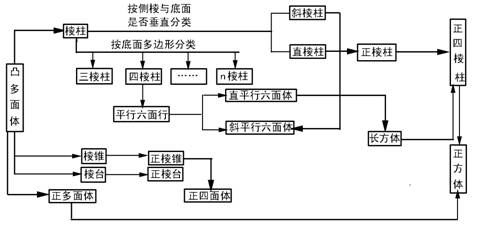
2.棱柱、棱锥、棱台的基本概念和主要性质
| 名 称 | 棱 柱 | 直棱柱 | 正棱柱 |
| 图 形 |
|
|
|
| 定义 | 有两个面互相平行，而其余每相邻两个面的交线都互相平行的 多面体 | 侧棱垂直于底面的棱柱 | 底面是正多边形的直棱柱 |
| 侧棱 | 平行且相等 | 平行且相等 | 平行且相等 |
| 侧面的形状 | 平行四边形 | 矩形 | 全等的矩形 |
| 对角面的形状 | 平行四边形 | 矩形 | 矩形 |
| 平行于底面的截面的形状 | 与底面全等的多边形 | 与底面全等的多边形 | 与底面全等的正多边形 |
| 名称 | 棱锥 | 正棱锥 | 棱台 | 正棱台 |
| 图形 |
|
|
|
|
| 定义 | 有一个面是多边形，其余各面是有一个公共顶点的三角形的多面体 | 底面是正多边形，且顶点在底面的射影是底面的射影是底面和截面之间的部分 | 用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分 | 由正棱锥截得的棱台 |
| 侧棱 | 相交于一点但不一定相等 | 相交于一点且相等 | 延长线交于一点 | 相等且延长线交于一点 |
| 侧面的形状 | 三角形 | 全等的等腰三角形 | 梯形 | 全等的等腰梯形 |
| 对角面的形状 | 三角形 | 等腰三角形 | 梯形 | 等腰梯形 |
| 平行于底的截面形状 | 与底面相似的多边形 | 与底面相似的正多边形 | 与底面相似的多边形 | 与底面相似的正多边形 |
| 其他性质 | 高过底面中心；侧棱与底面、侧面与底面、相邻两侧面所成角都相等 | 两底中心连线即高；侧棱与底面、侧面与底面、相邻两侧面所成角都相等 |
3.几种特殊四棱柱的特殊性质
| 名称 | 特殊性质 |
| 平行六面体 | 底面和侧面 都是平行四边行；四条对角线交于一点，且被该点平分 |
| 直平行六面体 | 侧棱垂直于底面，各侧面都是矩形；四条对角线交于一点，且被该点平分 |
| 长方体 | 底面和侧面都是矩形；四条对角线相等，交于一点，且被该点平分 |
| 正方体 | 棱长都相等，各面都是正方形四条对角线相等，交于一点，且被该点平分 |
4.面积和体积公式
下表中S表示面积，c′、c分别表示上、下底面周长，h表斜高，h′表示斜高，l表示侧棱长 .
| 名称 | 侧面积(S侧) | 全面积(S全) | 体 积(V) | |
| 棱柱 | 棱柱 | 直截面周长×l | S侧+2S底 | S底·h=S直截面·l |
| 直棱柱 | ch | S底·h | ||
| 棱锥 | 棱锥 | 各侧面积之和 | S侧+S底 |
|
| 正棱锥 |
| |||
| 棱台 | 棱台 | 各侧面面积之和 | S侧+S上底+S下底 |
|
| 正棱台 |
| |||
)5.正四面体的性质 设正四面体的棱长为a，则这个正四面体的
(1)全面积 S全=
a2；
(2)体积 V=
a3；
(3)对棱中点连线段的长 d=
a；
(4)相邻两面所成的二面角 α=arccos
(5)外接球半径 R=
a；
(6)内切球半径 r=
a.
(7)正四面体内任意一点到四个面的距离之和为定值(等于正四面体的高).
6.旋转体 圆柱、圆锥、圆台、球的公式
(1)面积和体积公式
| 圆柱 | 圆锥 | 圆台 | 球 | |
| S侧 | 2πrl | πrl | π(r1+r2)l | |
| S全 | 2πr(l+r) | πr(l+r) | π(r1+r2)l+π(r21+r22) | 4πR2 |
| V | πr2h(即πr2l) |
|
|
|
表中l、h分别表示母线、高，r表示圆柱、圆锥与球冠的底半径，r1、r2分别表示圆台 上、下底面半径，R表示半径.
(2)圆锥、圆台某些数量关系
②圆锥 圆锥轴截面两腰的夹角叫圆锥的顶角.
②圆台 如图，圆台母线与下底面所成角为α，母线为l，高为h，上、下底面半径分别为r ′、r，则
h=lsinα
r-r′=lcosα.
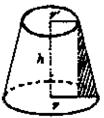
③球的截面 用一个平面去截一个球，截面是圆面.
(1)过球心的截面截得的圆叫做球的大圆；不经过球心的截面截得的圆叫做球的小圆.
(2)球心与截面圆圆心的连线垂直于截面.
(3)球心和截面距离d,球半径R，截面半径r有关系：
r=
.
(3)球冠、球带和球缺
①球缺 球面被平面所截得的一部分叫做球冠，截得的圆(圆周)叫做球冠的底，垂直于截面 的直径被截得的一段叫做相应球冠的高.
球冠也可以看作一段圆弧绕经过它的一个端点的直径旋转一周所成的曲面.
球冠的面积公式 若球的半径为R，球冠的高为h，则
S球冠=2πRh
其中h表示球冠的高，R是球冠所在的球的半径.
②球带 球面在两个平行截面之间的部分叫做球带.
球带也可以看作一段圆弧绕它所在的半圆的直径旋转一周所成的曲面.
球带的面积公式 若球的半径为R，球带的高为h，则
S球带=2πRh
③球缺 用一个平面截球体所得的部分叫做球缺，截面叫做球缺的底面，垂直于截面的直径 被截得的线段长叫做球缺的高.
球缺的体积公式 若球的半径为R，球缺的高h，底面半径为r，则
V球缺=πh2(3R-h)=
πh(3r2+h2)
三、知识点、能力点提示
(一)多面体
例1 如图，三棱柱ABC—A1B1C1中，若E、F分别为AB、AC 的中点，平面EB1C1将三棱柱分成体积为V1、V2的两部分，那么V1∶V2= .
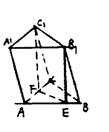
解：设三棱柱的高为h，上下底的面积为S，体积为V，则V=V1+V2＝Sh.
∵E、F分别为AB、AC的中点，
∴S△AEF=
S,
V1=h(S+S+
S)=
Sh
V2=Sh-V1=
Sh，
∴V1∶V2=7∶5.
例2 一个长方体全面积是20cm2，所有棱长的和是24cm，求长方体的对角线长.
解：设长方体的长、宽、高、对角线长分别为xcm、ycm、zcm、lcm
依题意得：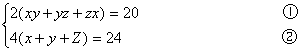
由②2得：x2+y2+z2+2xy+2yz+2xz=36 ③
由③-①得 x2+y2+z2=16
即l2=16 ∵l=4(cm).
例3 正四棱锥S-ABCD中，高SO＝2
，两相邻侧面所成角为γ ，tg
,(1)求侧棱与底面所成的角。(2)求侧棱 长、底面边长和斜高(见图)。
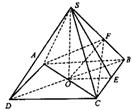
解
作CF⊥SB于F，连结AF，由△CFB≌△ABF及AF⊥SB，故∠AFC是相邻侧面所成二面角的平 面角，连结OF，则∠AFC＝γ，∠OFC＝
，在Rt△OCF与Rt△OBF中，t g＝
＝
(其中△SBO为SB与底面所成的角，设为α)。
故 sinα=
,α=60°
在 Rt△SOB中，侧棱SB＝
=4
，OB＝SO·ctgα ＝2，故边长BC＝·OB=4
在Rt△SEB中，斜高SE＝
＝2
例4 设正六棱锥的底面边长为1，侧棱长为
，那么它的体积为( )
A.6
B.2
C. D.2
解：由已知可得正六棱锥的底面积S=6×
设正六棱锥的高为h，则h=
=2.
∴V=×
×2=.
应选C.
例5 如果三棱锥S—ABC的底面是不等边三角形，侧 面与 底面所成的二面角都相等，且顶点S在底面的射影O在△ABC内，那么O是△ABC的( )
A.垂心 B.重心 C.外心 D .内心
解：作OE⊥AB，OF⊥BC，OM⊥CA
∵∠SEO=∠SFO=∠SMO,
∴△SEO≌△SFO≌△SMO.
∴OE=OF=OM.
∴O为△ABC的内心，应选D.
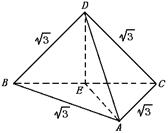
例6 已知三棱锥D-ABC的三个侧面与底面全等，且AB＝AC＝ ，BC＝2，则以BC为棱，以面BCD与面BCA为面的二面角的大小是( )
A.
B. 
C. 
D. 
解
如图因
AB＝AC＝，BC＝2又 △ABC≌△DBC≌△BDA
故
DB＝DC＝，DA＝2作DE⊥BC于E，由于△DBC中BD＝DC，所以E为BC中点又 △ABC中，AB＝AC，所以AE⊥BC于E所以 ∠DEA是二面D-BC-A的平面角
在 △DEA中，DA＝2，DE＝EA＝
＝
用余弦定理得
cos∠DEA＝
＝0
所以∠DEA＝
应选C
例7 已知三棱锥A—BCD的体积是V，棱BC的长是a，面ABC 和面 DBC的面积分别是S1和S2.设面ABC和面DBC所成的二面角是α，那么sinα= .
解：如图，作AO⊥面BCD于O，作OE⊥BC于E，连结AE.
由V=AO·S2，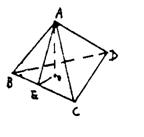
得AO=
又S1=
AE·BC，得AE=
由三垂线定理知，AE⊥BC，
∴∠AEO是二面角A—BC—D的平面角.
即∠AEO=α，
∴sinα=sin∠AEO=
.
例8 将边长为α的正方形ABCD沿对角线AC折起，使得BD＝α，则三棱锥D-AB C的体积为( )
A.
B. 
C.
D.
解
如图折起后的△DOB中，BD＝α，OD＝OB＝α
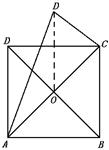
因 OD2+OB2＝DB2
故 ∠DOB＝90°
又 DO⊥AC，BO⊥AC
所以∠DOB是二面角D-AC-B的平面角。即面DAC⊥面BAC，从而DO⊥面ABC
所以VD-ABC＝·DO·S△ABC＝·α·α2＝α3
应选D.
例9 如图，在直四棱柱A1B1C1D1-ABCD 中，当底面四边形ABCD满足条件 时，有A1C⊥B1D1(注 ：填上你认为正确的一种条件即可，不必考虑所有可能的情形)。
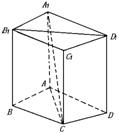
解 应填“AC⊥BD”或任何能推导这个条件的其它条件，例如，ABCD是正方形或菱形等。
因 A1A⊥底面ABCD，AC是A1C在底面ABCD的射影，
若 AC⊥BD，则根据三垂线定理有A1C⊥BD
又
B1D1∥BD
A1C⊥B1D1
故 应该填“AC⊥BD”
例10 已知长方体ABCD—A′B′C′D′中，棱AA′=5，AB=12，那么直 线B′C′和平面A′BCD′的距离是 .
解：如 图
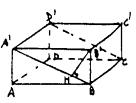
∵B′C′∥BC，B′C′∥面A′C，BC
面AC，
∴B′C′∥面A′C.
∴点B到平面A′BCD′的距离即直线B′C′到平面A′BCD′的距离.
作B′H⊥A′B于H，又CB⊥面A′ABB′，B′H面A′ABB′，B′H面A′B，所
以B′H⊥CB，从而B′H⊥平面A′BCD′.
∵B′H·A′B=B′A′·B′B，
∴B′H=
即直线B′C′到平面A′BCD′的距离是
.
(二)旋转体
例11 若干毫升水倒入底面半径为2cm的圆柱形器皿中，量得水面的高度为6c m。若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是( )
A.6cm
B.6cm C.2
cm
D.3
cm
解B.
例12 长方体一个顶点上三条棱的长度分别为3，4，5，且它的8个顶点都在 同一球面上，这个球的 表面积是( )
A.20π B.25π C.50π D.200 π
解：设长方体的对角线长为l，球半径为R，由已知及对称性知l=2R,
l=
，得R=
.
∴S球=4πR2=50π
应选C.
例13 已知圆台上下底圆周都在球上，且下底面过球 心，母线与底面所成的角为，则圆
台的体积与球体积之比为 。
解 如下图是轴截面图
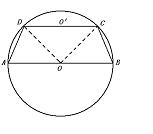
设球半径为R，连结OC
因 OC＝OB＝R，∠CBO＝60°
故 △OCB等边，∠COB＝60°
同理∠DOA＝60°，得△ODC等边
故
圆台上底半径r＝R
例14 如果等边圆柱(即底面直径与母线相等的圆柱)的体 积是16πcm3，那么它的底半径等于( )
A.4
cm B.4cm C.2·cm D.2cm
解：16π=πr2·(2r)=2πr3，得r=2(cm)
应选D.
例15 圆柱轴截面的周长1为定值，那么圆柱体积的最 大值是( )
A.()3π B.()3π C.()3π D. ()3π
解：设r为底半径，l为母线.
由4r+2l=1，得l=
V=πr2l=
π(2r)(2r)(2l)≤π(
)3
=π·(
)3=π·()3=()3 π.
等号仅当2r=2l即r=l=时成立.
应选A.
例16 设圆锥底面圆周上两点A、B间的距离为2，圆锥 顶点到直线AB的距离为，AB和圆锥的轴的距离为1,则该圆锥的体积为
.
解：如图
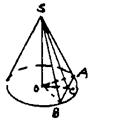
O为底面圆心，OC⊥AB于C.
由OA=OB得C为AB中点，
由SA=SB，C为AB中点得SC⊥AB于C.
∴OC=1,SC=,AC=CB=1,
SO=
，
OB=
.
∴V=π·OB2·SO=π()2=
π.
例17 在一个实心圆锥体的零部件，它的轴截面是边长为10厘米的等边三角 形，现要在它的整个表面镀上一层防腐材料，已知每平方厘米的工料价为0.1元，则需要费用 元(π取3.2).
解：设圆锥的底半径为r,由已知有r=5cm,母线长为10cm.
S全=π·52+π·5·10=75π=240(cm2)
∴工料价为240×0.1=24元.
例18 圆锥母线长为l，侧面展开圆心角为240°，该圆锥的体积是( )
A.
π B.
π C.
π D.
π
解：设圆锥底半径为r，由已知有
240°=
π=
，得r=
.
∴h=
.
∴V=πr2h=π()2·
=π
应选C。
【同步达纲练习】
(一)选择题
1.给出下列命题：
①底面是正多边形的棱锥是正棱锥；
②侧棱都相等的棱锥是正棱锥；
③侧棱和底面成等角的棱锥是正棱锥；
④侧面和底面所成二面角都相等的棱锥是正棱锥，其中正确命题的个数是( )
A.0 B.1 C.2 D.3
2.两球体积和是12π，且两球大圆周长的和是6π，则这两个球半径的差是( )
A.3 B.2 C.1 D.0.5
3.地球表面北纬60°圈上有A、B两点，它们的经度差为180°，A、B两点沿纬度圈的距离与 地球表面A、B两点最短距离的比是( )
A.3：2 B.2：3 C.3：4 D.4：3
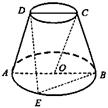
4.如图，已知圆台的轴截面ABCD，∠ABC＝60°，AB＝12，CD＝6 ，点E是下底面圆O上的一点，∠ABE＝30°，则DE与CO所成角α的正切的值等于( )
A.
B.
C.
D.
5.球O的半径R，A、B、C为球面上三点，A与B、A与C的球面距离为
，B与C的球面距离为R，则球O在二面角B-OA-C内的
部分的体积是(
)
A.
πR3
B.πR3
C.
πR3
D.
πR3
6.三棱锥A-BCD的高AH=3a，且H是底面△BCD的垂心，若AB=AC，二面角A-B C-D为60°，G为△ABC的重心，则HG的长为( )
A.
a B.a C. a D. a
7.底面半径为R，高为H的圆锥的内接正方体的棱长为( )
A.
B.
C.
D.
8.如下图，已知AA′B′B是圆柱的轴截面，C是底面圆周上一点，且 ∠CAB＝α，∠CA′B＝β，∠ABA′＝θ，则α、β、θ三个角之间的关第是( )
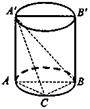
A.sinαcosθ=sinβ B.cosαcosθ=cosβ
C.sinα=sinβcosθ D.cosα=cosβcosθ
9.用一张半径为R的圆形滤纸，做一个容量最大的过滤器(圆锥体)，则将这个圆形滤纸剪去 一个扇形的中心角θ(弧度)应是( )
A.2π-π
B.2π-
π
C.
D.
10.正四棱台ABCD-A1B1C1D1的上底边长：侧棱长：下底边长＝1∶2∶3，则其面对 角线AD1与B1C所成角的余弦值为( )
A.
B.
C.-
D.
(二)填空题
11.圆锥的侧面展开图是一个半圆，有一个半球的底面恰好为该圆锥的底面，半球面将圆锥 侧面分成上、下两部分，这两部分面积分别是S1、S2，则S1∶S2＝ .
12.把一个大金属球 表面涂漆，需油漆2.4kg，若把这个金属球熔化， 制成 64个半径相等的小金属球(设损耗为零)，将这些小金属球表面涂漆，需用油漆 .
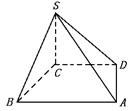
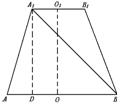
13.如图，一块铁皮呈等腰梯形状，两底分别为4a，2a，高SC 为a，S是AA′的中点，将梯 形沿虚线折成一个四棱锥S-ABCD的侧面(如图)(A重合于A′)，该四棱锥的体积为 .
14.正四棱台ABCD-A1B1C1D1，上底AB=1，下底A1B1=2，侧棱AA1与底面成60 °角，则侧面梯形ABB1A1的对角线BA1与下底面所成的角为 .
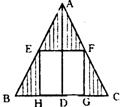
15.如图，在正三角形ABC中，E、F分别是AB、AC的中点，AD⊥BC，EH⊥BC，FG⊥BC，D 、H、G为垂足，若将正△ABC绕AD旋转一周所得圆锥的体积记为V，则其中由阴影部分所产生 的旋转体的体积与V的比值是 .
(三)解答题
16.设圆台的高为h，母线与下底所成的角为α，轴截面中一条对角线垂直于腰，求圆台的 侧面积.
17.已知球的外切圆台的体积是球体积的
倍，求这个圆台的母线与底 面成角的大小.
18.求半径为R的球内接圆锥侧面积的最大值.
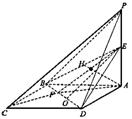
19.如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，AB＝5cm， AD＝8cm，∠BAD＝60°，PA＝
cm，且PA⊥平面ABCD，点E在PA上，且 PC∥平面BED.
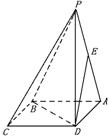
①求这个四棱锥被截面BED分成两部分的体积；
②求顶点A到截面BED的距离。
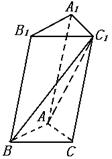
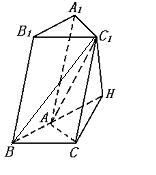
20.如图，斜三棱柱ABC-A1B1C1的底面是Rt△ABC，∠A＝90 °，且BC1⊥AC，作C1 H⊥底面ABC，垂足为H。①试判断H点的位置，并说明理由。②若AB＝AC＝2，AC1＝2，侧棱与底面成60°角，求三棱柱ABC-A1B1C1的体积.
21.已知AA′B′B是圆柱的轴截面，C是上底面圆周上不同于A，B的一点.①求证平面BA′ C⊥平面AA′C；②当棱锥A′-ABC的体积V′和圆柱的体积V的比是1：2，求 二面角B-AA′-C的大小；③设A-A′B-C为α，又∠CAB=β，∠CA′B=γ，求证sinα=
.
参考答案
【同步达纲练习】
(一) 1.A 2.C 3.A 4.C 5.C 6.B 7.C 8.A
9.B 10.D
提示：
5.可求得二面角B-OA-C的平面角就是∠BOC=60°，因此两个半圆面所夹的体积是球体积的.
(二)11.1∶3 12.9.6kg 13.
a3 14
.arctg
15.5∶8
(三)16.设圆台的截面A1ABB1，上、下底半径分别为r和R， 母线长为l，A1D⊥AB于
D，则A1D＝h，∠A1AB＝α，则BD＝h·tgα，而BD＝R+r，即BD＝R+r＝h·tgα，t=h· cscα.
S侧＝π(R+r)l=πh2secα.
17.画出轴截面图，设圆柱上、下底半径分别为a、b，可依题设条件求得内切球半径R=
，由
得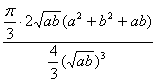
=，化简得b=2a，易知母线与底面所成角θ的正切值tgθ=
=2，因此母线与底面所成角为arctg2.
18.设圆锥顶角为2α，则母线l=2Rcosα，底面圆半径r=Rsinα，则 圆锥侧面积.
S=πγl= 2πR2sin2αcosα= 4πR2sinαcos2α
其中令y=sinαcos2α，则
y2=sin2αcos4α=sin2α(1-sin2 α)2
=·2sin2α·(1-sin2α)(1-sin2α)
≤〔
〕3=
当2sin2α=1-sin2α即sinα=
时，等号成立，
∴y≤
∴S≤
πR2
即圆锥侧面积的最大值是πR2. 
19.①如图，AB∩BD＝O，则OE是平面BED和平面APC的交线，由PC∥ OE E是PA中点，从而EA＝
。易知
VE-ABD＝
，VEPBCD＝VP-ABD＝
(cm3).
②作AF⊥BD，垂足为F，连EF，易证平面EAF⊥平面BED，作AH⊥AEF中，AE＝cm，AF＝
cm，EF＝cm，可知∠FEA＝60°，因此AH＝AE。sin60°＝
(cm)，即为所求A到平面BED的距离.
20.①C1H⊥平面ABC，连结BH，则BH是BC1是在平面ABC的射影。
BC1⊥AC，BH⊥AC，又BA⊥AC，而在平面ABC内，过B只有一条直线垂直于AC，故BA，BH重 合，故H点在BA直线上。
②连结CH，则∠C1CH＝60°，设C1H＝x，则CH＝x，在Rt△CAH中，AH1＝(x)2-22，在Rt△C1 HA中，AH1＝(2)2-x2，x2-4＝28-x2，x 2＝24，x＝2，又S△ABC＝×2×2＝2，V棱柱＝2·2＝4。
21.①略. ②易知∠BAC是二面角B-AA′-C的平面角，设圆柱底半径为r，高为h，∠CAB=β，则VA ′-ABC=·S△ABC·h=··2sinβ·2rcosβ·h=r2s in2β又圆柱体积V=πr2h，由VA′-ABC：V=1:2，得sin2β=，2β=60°或120°，故二面角B-AA′-C，为60°或30°.
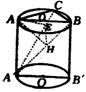
③由①得平面BA′⊥平面AA′C，作AE⊥A′C，则AE⊥平面BA′C，作EH⊥A′B，连结AH，可 知∠AHE是二面角A-A′B-C的平面角，∠AHE=α，sinα=
，其中AE= AC·cos∠AA′C=2rcosβ·
；AH=AB·cos∠AA′B=2r·
，∴
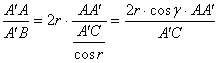，即sinα=.