高考数学仿真试题(八)答案
一、1.C 2.D 3.A 4.B 5.B 6.C 7.C 8.B 9.D 10.B 11.A 12.C
二、13. 60° 14.x=2 15.－11
16.①②
③,①③②
17.解：（Ⅰ）设1－w=－bi(b＞0) 1分
∴w=1+bi，∴i－1－bi=1
即1+(1－b)2=1
∴b=1，∴w=1+i 6分
（Ⅱ）λ=z－w=cosθ+isinθ－1－i=
≤
10分
∴λmax=
+1
18.（Ⅰ）n≥2 Sn2=(Sn－Sn－1)(Sn－
) 2分
∴
即
（n≥2） 4分
∴
∴
6分
（Ⅱ）
10分
12分
19.（Ⅰ）证明：易证AD⊥面BB1C1C
∴面ADC1⊥面BB1C1C 4分
（Ⅱ）arcsin
8分
（Ⅲ）
12分
20.解：（Ⅰ）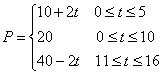
6分
（Ⅱ）
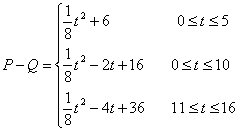10分
t=5时，Lmax=
，即第五个月销售利润最大. 12分
21.解：（Ⅰ）设P(x0,y0)是y=f(x)图象上点，Q（x,y）,则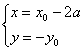
，
∴
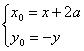∴－y=loga(x+2a－3a)，∴y=loga
(x＞a)
5分
（Ⅱ）
∴x＞3a
∵f(x)与g(x)在［a+2,a+3］上有意义.
∴3a＜a+2
∴0＜a＜1 6分
∵f(x)－g(x)≤1恒成立loga(x－3a)(x－a)≤1恒成立.
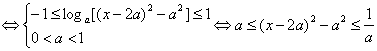8分
对x∈［a+2,a+3］上恒成立，令h(x)=(x－2a)2－a2
其对称轴x=2a,2a＜2,2＜a+2
∴当x∈［a+2,a+3］
hmin(x)=h(a+2)，hmax=h(a+3)
∴原问题等价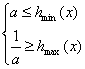
10分
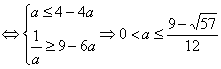12分
22.解：（Ⅰ）设椭圆E的方程为
(a＞b＞0)，由e=
∴a2=3b2
故椭圆方程x2+3y2=3b2 1分
设A(x1,y1)、B(x2,y2),由于点C（－1，0）分有向线段
的比为2，
∴
|
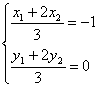
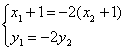3分
由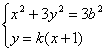
消去y整理并化简得
(3k2+1)x2+6k2x+3k2－3b2=0
由直线l与椭圆E相交于A（x1,y1）,B(x2,y2)两点
|
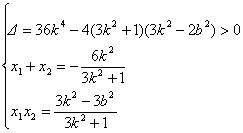5分
而S△OAB
⑥
由①④得:x2+1=－
，代入⑥得：S△OAB=
8分
（Ⅱ）因S△OAB=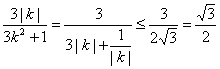
,当且仅当
S△OAB取得最大值 10分
此时x1+x2=－1,又∵
=－1
∴x1=1,x2=－2
将x1,x2及k2=
代入⑤得3b2=5
∴椭圆方程x2+3y2=5 14分