高考数学仿真试题(二)答案
一、1.D 2.A 3.D 4.B 5.C 6.B 7.D 8.A 9.C 10.C 11.B 12.A
二、13. 13 4
14.
15.sin210°+cos240°+sin10°cos40°=
16.①③
②
17.解：已知M∩N≠
.∴M、N中至少有一个元素相等即有cosθ+(4-m2)i
=m+(λ+sinθ)i 2分
从而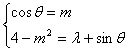
4分
∴λ=4-cos2θ-sinθ=(sinθ-
)2+
8分
∵sinθ∈［-1,1］ ∴当sinθ=时，λmin=,当sinθ=-1时，λmax=5
∴λ的取值范围为［，5］ 12分
18.解：（Ⅰ）a1=S1=p(a1-1)
∴a1=
1分
n≥2,an=Sn-Sn-1=p(an-an-1)
∴
∴{an}是以a1=为首项，公比为q=的等比数列 4分
∴an=()n 5分
(Ⅱ)由已知a1=b1,a2<b2,
∴=2+q,( )2<4+q 7分
消去q整理（）2--2<0
∴-1<<2 ∴p<或p>2 10分
∵q=≠0 ∴p≠0
∴p的范围为（-∞,0）∪(0, )∪(2,+∞) 12分
19.（Ⅰ）证明：∵E是C1D1的中点，∴C1E=D1E=a,又由直四棱柱的性质得BC⊥面CC1D1D，
∴EC=
a,BE=
a,DE=a,又BD=
a,
∴△BDE是直角三角形,△DEC也是直角三角形,∴DE⊥EC,DE⊥BE,∴DE⊥面BEC，又DE
平面BDE
∴平面BCE⊥平面BDE 4分
(Ⅱ)解：取CD的中点E′ ∴EE′⊥面ABCD，∴△BED在面AC内的射影是
△E′BD,设二面角E—BD—C的大小为θ,∴cosθ=
又∵S△BDE=DE·BE=
a2，S△BE′D=a2,
∴cosθ=
∴θ=arccos 8分
(Ⅲ)解：V
—BDE=VD—BE=V
—BE=
D1E·S△BE=a·
a=
a3.
故V—BDE=a3 12分
20.解：（Ⅰ）y=
∵x<-2，∴x=-
即y=f-1(x)=-
(x>0) 4分
(Ⅱ)∵
∴
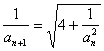=4
∴{
}是公差为4的等差数列
∵a1=1 ∴=
+4(n-1)=4n-3
∵an>0 ∴an=
8分
(Ⅲ)bn=Sn+1-Sn=an+12=
由bn<
得m>
对于n∈N成立
∵≤5 ∴m>5,存在最小正数m=6,使得对任意n∈N有bn<成立 12分
21.（Ⅰ）解：∵g(t)为常数 ∴g(0)-
=0
∴g(0)=
2分
(Ⅱ)证明：证得0<t1<t2,则g(t1)-g(t2)=［g(0)-
］e
-［g(0)- ］e
=［g(0)- ］［e-e］=［g(0)- ］
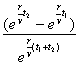
∵g(0)·<0,t1<t2,e
>e
∴g(t1)<g(t2) 6分
故湖水污染质量分数随时间变化而增加，污染越来越严重 8分
(Ⅲ)解：污染停止即P=0，g(t)=g(0)·e
,设经过t天能使湖水污染下降到初始污染水平5%即g(t)=5% g(0)
∴
=e，∴t=
ln20，
即需要 ln20天 12分
22.解：（Ⅰ）∵（x+1）2=-4(y-1)
∴F1(-1,0) 2分
（Ⅱ）∵A、B在双曲线上，∴AF1-AF2=BF1-BF2，2-AF2=2-BF2
若2-AF2=2-BF2
∴AF2=BF2则点F2在线段AB的中垂线上
∴点F2的轨迹方程为x=-1(y≠0,y≠4) 6分
若2-AF2=BF2-2
∴AF2+BF2=4
∴点F2的轨迹是以A、B为焦点，a=2,c=2,b2=4,中心为（-1，2）的椭圆，其方程为
=1(y≠0,y≠4)（草图略） 10分
|
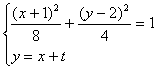
将②代入①消去y得到
3x2+(4t-6)x+2t2-8t+1=0
Δ=4(2t-3)2-12(2t2-8t+1)<0
t2-6t-3>0
∴t>3+2
或t<3-2
又直线过点（-1，0），（-1，4）时，t=1或t=5
∴t的范围为（-∞,3-2）∪(3+2,+∞)∪{1,5} 14分