高三数学训练题（七）
一、选择题：本大题共12小题，每小题5分，共60分．
1. 已知
是等差数列，且
，
，此数列的首项与公差依次为( )
（A）19，－2 （B）21，－2 （C）15，－1 （D）16，－1
2. 在等比数列中，
，
，则
( )
（A）45
（B）171 （C）
（D）192
3. 已知数列首项为
，且
，则
为
( )
（A）7 （B）15
（C）30
（D）31
4. 函数
的单调递增区间是
( )
（A）
，
（B）
， （C）
，
（D），
5. 在等差数列中，
、
是方程
的两个根，则
是 ( )
（A）30
（B）15
（C）50 （D）25
6. 函数
的值域是
( )
（A）， （B），
（C）， （D）
，
7. 
是
成等比数列的
( )
（A）充分非必要条件
（B） 必要非充分条件
（C）充要条件
（D） 既非充分也非必要条件
8. 若某等差数列中，前7项和为48，前14项和为72，则前21项和为 ( )
（A）96 （B）72
（C）60
（D）48
9. 在等比数列中，若
，
，则的值
( )
（A）是3或－3 （B） 是3 （C）
是－3 （D）不存在
10. 函数
的图象大致是 ( )
（A）
（B）
（C）
（D）
11. 在等比数列
中，已知
，则
的值为
( )
（A）
（B）
（C）
（D）
12. 设函数
定义在R上，且
是偶函数， 
是奇函数，则
=
( )
（A）0
（B）1
（C）2003 （D）－2003
二、填空题：本大题共4小题，每小题4分，共16分．
13. 设全集U=R，集合
，则
＿＿＿＿＿．
14. 在数列中，已知
，那么使其前
项和
取最大值时的值等于＿＿＿＿＿．
15. 设
，则使
的最小正整数的值是＿＿＿＿＿．
16. 使关于
的方程
有正根的实数
的取值范围是＿＿＿＿＿．
三、解答题：本大题共6小题，共74分，解答应写出文字说明或演算步骤．
17.（本小题满分10分）
已知函数
为一次函数， 
是
和
的等比中项，且
，
求
，
的表达式．
18. （本小题满分12分）将函数
的图象向右平移2个单位，再向上平移1个单位，可得到函数g（x）的图象．写出
的解析式及其定义域，并求其反函数
．
19.（本小题满分12分）已知是定义在Ｒ上的奇函数，当
时，
，
（1）求函数； （2）解不等式
．
20.（本小题满分12分）数列是首项为1的等差数列，数列
是首项为1的等比数列，设
，且数列
的前三项依次为1，4，12，
（1）求数列、的通项公式；
（2）若数列是递增的等差数列，求数列的前项的和．
21.（本小题满分14分）８月份，有一新款服装投入某商场销售，８月1日该款服装仅销售出3件，８月2日售出6件，８月3日售出9件，８月４日售出12件，尔后，每天售出的件数分别递增3件，直到日销售量达到最大（只有一天）后，每天销售的件数开始下降，分别递减2件，到８月3１日也刚好售出3件．
⑴问８月几号该款服装销售件数最多？其最大值是多少？
⑵按规律，当该商场销售此服装达到200件时，社会上就流行，而日销售量连续下降并低于20件时，则流行消失，问该款服装在社会上流行几天？说明理由．
22.（本小题满分14分）已知
，函数
的最小值与最大值之和为
，又数列
的前项的和是
．
（1）求数列的通项公式； （2）求证：数列是等比数列；
（3）设
，试问数列有没有最大项？如果有，求出这个最大项，如果没有，请说明理由．
高三数学训练题07答案
一、ADDAB BBBAC CA
二、
，12；11；
三、17．
；
。
18．
（
；
。
19．（1）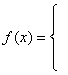
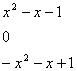
（2）
20．（1）
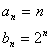或
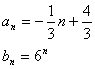
（2）
21．（1）8月13日，39件；
（2）从12日到22日共11天。
22．（1）
；
（2）
；
（3）当
或
时有最大值。