高三数学训练题(五)
一、选择题:本大题共12小题,每小题5分,共60分.
1、如果集合![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2、映射f:A→B,如果满足集合B中的任意一个元素在A中都有原象,则称为“满射”。已知集合A中有4个元素,集合B中有3个元素,那么从A到B的不同满射的个数为
A.24 B.6 C. 36 D.72 ( )
3、若![]()
A.关于直线y=x对称 B.关于x轴对称 ( )
C.关于y轴对称 D.关于原点对称
4、函数y=x2的图象按向量![]() =(2,1)平移后得到的图象的函数表达式为
=(2,1)平移后得到的图象的函数表达式为
A. y=(x—2)2—1 B.y=(x+2)2—1 ( )
C. y=(x—2)2+1 D. y=(x+2)2+1
5、若函数f(x)=lg(x2-ax-3)在(-∞,-1 )上是减函数,则a的取值范围是 ( )
A.a>2 B.a<2 C.a≥2 D.a≤2
6、函数f(x)=x-![]() 在(1,+∞)上是增函数,则实数p的取值范围是 ( )
在(1,+∞)上是增函数,则实数p的取值范围是 ( )
A.[-1,+∞![]() B.[1,+∞
B.[1,+∞![]() C.
C. ![]() -∞,-1] D.
-∞,-1] D.![]() -∞,1]
-∞,1]
7、设函数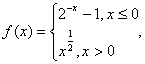 若f(x0)<1,则x0的取值范围是
( )
若f(x0)<1,则x0的取值范围是
( )
A.(—1,1) B.(—1,+∞)
C.(—∞,—2)∪(—∞,0) D.(—∞,—1)∪(1,+∞)
8、设a>0,![]() ,曲线
,曲线![]() 在点P(x0,f(x0))处切线的倾斜角的取值范围为
在点P(x0,f(x0))处切线的倾斜角的取值范围为![]() ,则P到曲线y=f(x)对称轴距离的取值范围为
( )
,则P到曲线y=f(x)对称轴距离的取值范围为
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、设函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
那么![]() 值等于 ( )
值等于 ( )
A.-1 B.-2 C.![]() D.
D.![]()
10、定义在R上的函数f(x)满足f(-x)=f(x),f(x)=-f(x+1),且在[0,1]上单调递减,则
A. f(![]() )<f(
)<f(![]() )<f(
)<f(![]() )
B.f(
)
B.f(![]() )<f(
)<f(![]() )<f(
)<f(![]() ) ( )
) ( )
C. f(![]() )<f(
)<f(![]() )<f(
)<f(![]() ) D.f(
) D.f(![]() )<f(
)<f(![]() )<f(
)<f(![]() )
)
11、任取x1,x2∈[a,b],且x1≠x2,若![]() ,称f(x) 是[a,b]上的凸函数,则下列图像中,是凸函数图像的是
( )
,称f(x) 是[a,b]上的凸函数,则下列图像中,是凸函数图像的是
( )
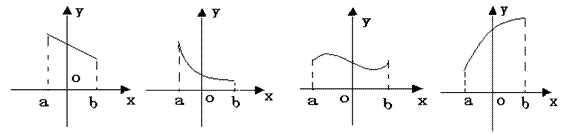 |
A. B. C. D.
12、设函数![]()
![]()
![]()
![]() + b
+ b![]() + c 给出四个命题:
+ c 给出四个命题:
① c = 0时,y![]()
![]() 是奇函数 ② b
是奇函数 ② b![]() 0 , c >0时,方程
0 , c >0时,方程![]()
![]() 0 只有一个实根
0 只有一个实根
③ y![]()
![]() 的图象关于(0 , c)对称 ④ 方程
的图象关于(0 , c)对称 ④ 方程![]()
![]() 0至多两个实根
0至多两个实根
上述四个命题中所有正确的命题是: ( )
A.①、④ B.①、③ C.①、②、③ D.①、②、④
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13、函数![]() 的图象与其反函数图像的交点坐标为 。
的图象与其反函数图像的交点坐标为 。
14、函数![]() 的最大值是
。
的最大值是
。
15、若对于任意a![]() [-1,1], 函数f(x) = x
[-1,1], 函数f(x) = x![]() + (a-4)x + 4-2a的值恒大于零, 则x的取值范围是
。
+ (a-4)x + 4-2a的值恒大于零, 则x的取值范围是
。
16、如果函数f(x)的定义域为R,对于![]()
是不大于5的正整数,当x>-1时,f(x)>0. 那么具有这种性质的函数
f(x)= 。
(注:填上你认为正确的一个函数即可,不必考虑所有可能的情形).
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17、二次函数f(x)满足![]() 且f(0)=1.
且f(0)=1.
(1) 求f(x)的解析式;
(2)
在区间![]() 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
18、(本小题12分)一块铁板长为80cm,宽为50cm,从四角处截掉四个同样的正方形,然后做成一个无盖的水箱,问正方形的边长为多少时,使水箱容积最大?
19、已知函数![]() 的值域是
的值域是![]() ,求实数m,n的值。
,求实数m,n的值。
20、设函数![]() (a为实数).
(a为实数).
(1)
若a<0,用函数单调性定义证明:![]() 在
在![]() 上是增函数;
上是增函数;
(2)
若a=0,![]() 的图象与
的图象与![]() 的图象关于直线y=x对称,求函数
的图象关于直线y=x对称,求函数![]() 的解析式.
的解析式.
21、设![]() ,a,b是满足
,a,b是满足![]() 的实数,其中
的实数,其中![]() 。
。
(1) 求证:![]()
(2) 求证:![]()
22、已知f(x)在(-1,1)上有定义,f(![]() )=-1,且满足对任意实数x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足对任意实数x,y∈(-1,1)有f(x)+f(y)=f(![]() )
)
(Ⅰ)证明:f(x)在(-1,1)上为奇函数;
(Ⅱ)对数列x1=![]() ,xn+1=
,xn+1=![]() ,求f(xn)关于n的表达式;
,求f(xn)关于n的表达式;
(Ⅲ)求证![]()
高三数学训练题05答案
一、 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | C | C | C | A | A | B | B | B | D | C |
二、 填空题
13、(0,0),(1,1)
14、![]()
15、(-∞‚1)∪(3,+∞)
16、x+6或2x+6或3x+6或4x+6或5x+6
三、 解答题
17、解 (1)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,所以![]() ,∴f(x)=x2-x+1.
,∴f(x)=x2-x+1.
(2)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1,1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x=,所以g(x) 在[-1,1]上递减.
故只需g(1)>0,即12-3×1+1-m>0,解得m<-1.
18、解 设截去的小正方形的边长为x㎝,则水箱的底面长为(80-2x)㎝,宽为(50-2x)㎝.
由题意水箱的容积V(x)=x(80-2x)(50-2x),(0<x<25).
整理得V(x)=4x3-260x2+4000x,V´(x)=12x2-520x+4000,
令V´(x)=0得x1=(舍去),x2=10,当x∈(0,10)时, V´(x)>0; 当x∈(10,25)时,
V´(x)<0.所以当x=10时, V(x)取得极大值,也是最大值.
答:当截去的小正方形的边长为10㎝时水箱的容积最大.
19、解
由![]() 得x2+(m-y)x+3-ny=0有解.
得x2+(m-y)x+3-ny=0有解.
所以![]() ,即
,即![]() .
.
因此y的范围就是上述不等式的解集,由题意y≤-2或y≥4,
所以-2和4是方程![]() 的两根.
的两根.
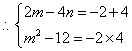 ,解得
,解得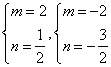 ,均适合.
,均适合.
20、解 (1)设任意实数x1<x2,则f(x1)- f(x2)=![]()
=![]()
=![]()
![]()
![]() .
.
又![]() ,∴f(x1)- f(x2)<0,所以f(x)是增函数.
,∴f(x1)- f(x2)<0,所以f(x)是增函数.
(2)当a=0时,y=f(x)=2x-1,∴2x=y+1, ∴x=log2(y+1),
y=g(x)= log2(x+1).
21、证明(1)∵f(a)=f(b),∴lga=lgb,∴lga= lgb,或lga= -lgb.
∵0<a<b, ∴lga= -lgb,即lga+lgb=0,所以ab=1.
又∵0<a<b, ∴a<1<b;
(2)∵![]() ,∴由条件得
,∴由条件得![]() ,
,
∴![]() ,∵0<a<1,∴a2<1,
,∵0<a<1,∴a2<1,
∴![]() ;
;
又![]() ,∴
,∴![]()
22、证明(Ⅰ)令x=y=0得f(0)+f(0)=f(0),所以f(0)=0.
令y=-x得f(x)+f(-x)=f(0)=0,即f(-x)=-f(x)在(-1,1)上恒成立.
由奇函数定义知,f(x)是(-1,1)上的奇函数.
解 (Ⅱ)∵xn+1=![]() ,∴f(xn+1)=
f(
,∴f(xn+1)=
f(![]() )=f(
)=f(![]() )=2 f(xn).
)=2 f(xn).
∴f(xn)是以f(x1)= f()=-1为首项,公比为2的等比数列.
∴f(xn)=-2n-1.
证明(Ⅲ)左边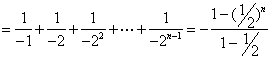 ,
,
![]() ,
,
右边![]() ,显然
,显然![]() ,
,
∴![]()