第二次诊断性数学考试
数 学 (理工类)
本试卷分为试题卷和答题卷两部分，其中试题卷由第I卷（选择题）和第Ⅱ卷(非选择题) 组成，共4页；答题卷共4页．满分100分．考试结束后将答题卡和答题卷一并交回．
第Ⅰ卷(选择题，共48分)
注意事项：
1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上．
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦擦干净后，再选涂其他答案，不能答在试题卷上．
3．参考公式：
如果事件A、B互斥，那么P(A+B)=P(A)+P(B)；
如果事件A、B相互独立，那么P(A·B)=P(A)·P(B)；
如果事件A在一次试验中发生的概率为P，那么n次独立重复试验中恰好发生k次的概率：
；
正棱锥、圆锥的侧面积公式
其中c表示底面周长，l表示斜高或母线长；
球的体积公式
其中R表示球的半径．
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中, 只有一项是符合题目要求的, 把它选出来填涂在答题卡上．
1．不等式 
的解集是
A．{x︱x＞－2
B．{x︱x＜－2
C．{x︱－2＜x＜1或x＞1
D．{x︱x＜－2或x＞1
2．若a＞b＞0，则下列不等式中总成立的是
A．
B．
C．
D．
3．下列极限中，其值等于2的是
A．
B．
C．
D．
4．设不重合两条直线l1：ax+by+c=0与直线l2：mx+ny+p=0，则an=bm是直线l1∥l2的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
5．在平面上，已知点A(2，1)，B(0，2)，C(－2，1)，O(0，0)．给出下面的结论：
①
②
③
其中正确结论的个数是
A．1个 B．2个 C．3个 D．0个
6．已知数列{an}的通项公式是
，其中a、b均为正常数，那么an与
的大小关系是
A．
B． 
C．
D．与a、b的取值有关
7．设
且17q 的终边与q 的终边相同，则tanq =
A．
－1 B． C．+1 D．1
8．方程 x (x2 + y2－3) = 0与x2 + (x2 + y2－3)2 = 0所表示的曲线是
A．都表示一条直线和一个圆
B．都表示两个点
C．前者是两个点，后者是一条直线和一个圆
D．前者是一条直线和一个圆，后者是两个点
9．设a、b是某一锐角三角形的两个内角，则必有
A．sina＜cosb且sinb＜cosa
B．sina＜cosb且sinb＞cosa
C．sina＞cosb且sinb＞cosa
D．sina＞cosb且sinb＜cosa
10．函数y=x+cosx的大致图象是
 |
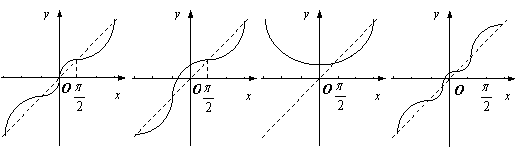A． B． C． D．
11．由方程 
确定的函数y=f(x)在(－∞，+∞)上是
A．奇函数 B．偶函数 C．增函数 D．减函数
12．已知a，b，c∈R，若
，且
，则下列结论成立的是
A．a，b，c同号 B．b，c同号，a与它们异号
C．b，c 同号，a不能确定 D．a，b，c的符号都不能确定
第Ⅱ卷 (非选择题 共90分)
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
13．已知目标函数S = 2x + y，则函数S在条件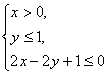
下的最大值为
．
14．已知
，那么角a是第 象限的角．
15．设a、b、c是△ABC中ÐA、ÐB、ÐC的对边，S是△ABC的面积，若a=4，b=5，
，则c = ．
16．已知命题：“若数列{an}为等差数列，且am=a，an=b (m≠n，m，n∈N+)，则
”．现已知数列{bn}(bn＞0，n∈N+)为等比数列，且bm=a，bn=b (m≠n，m，n∈N+)，若类比上述结论，则可得到bm+n= ．
三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．
17．(本题满分12分) 已知数列{an}的各项均为正数，且前n项和Sn满足
．若a2、a4、a9 成等比数列，求数列{an}的通项公式．
18．(本题满分12分) 已知A是圆x2 + y2 = 4上任一点，AB垂直于x轴，交x轴于点B．以A为圆心、AB为半径作圆交已知圆于C、D，连结CD交AB于点P，求点P的轨迹方程．
19．(本题满分12分) 设平面内的向量
, 
, 
，点P是直线OM上的一个动点，求当
取最小值时，
的坐标及ÐAPB的余弦值．
20．(本题满分12分) 某地计划从今年起填湖围造一部分生产和生活用地.若填湖费、购置排水设备费等所需经费与当年所填湖造地面积x (亩)的平方成正比，其比例系数为a．设每亩水面的年平均经济收益为b元，填湖造地后的每亩土地的年平均收益为c元(其中a，b，c均为常数)．
(Ⅰ) 若按计划填湖造地，且使得今年的收益不小于支出，试求所填面积x的最大值．
(Ⅱ) 如果填湖造地面积按每年1％的速度减少，为保证水面的畜洪能力和环保要求，填湖造地的总面积永远不能超过现有水面面积的25％，求今年填湖造地的面积最多只能占现有水面的百分之几.
21．(本题满分12分) 证明： 
．
22．(本题满分14分) 试利用“对数函数y = log a x在(0，+∞)上的单调性质：0＜x1＜x2 Û log a x1＜log a x2 (a＞1)；0＜x1＜x2 Û log a x1＞log a x2 (0＜a＜1
” 解决下列问题：
已知二次函数f(x)的图象开口向下,且对任意实数x有f(2－x)=f(2+x), 解关于x的不等式：
．
第二次诊断性考试
数学(理)参考解答及评分标准
一、 选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，把它选出来填涂在答题卡上．
CABC BADD CBDA
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
13．2 14．二或四 15．
或
16． 
三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．
17．解 ∵ 对任意nÎN*，有 ， (1)
∴ 当n=1时，有 
，
解得 a1 = 1 或a1 = 2． ……………… 3分
当n≥2时，有 
．
(2)
于是，由 (1)－(2) 整理可得 (an + an－1)(an－an－1－3)=0．
因为{an}的各项均为正数，所以 an－an－1 = 3． …………… 8分
当a1 = 1时，an =1+3(n－1)=3n－2，此时a42=a2a9成立．
当a1 = 2时，an =2+3(n－1)=3n－1，此时a42=a2a9不成立，故a1=2舍去．
所以an=3n－2． ……………… 12分
18．
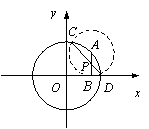解 设点A的坐标为A(2cosa，2sina)，
则以A为圆心、AB为半径的圆的方程为
(x－2cosa)2 + (y－2sina)2 = 4sin2a． ……… 4分
联立已知圆x2 + y2 = 4的方程，相减，
可得公共弦CD的方程为
xcosa + ysina = 1+ cos2a． (1) ……… 8分
而AB的方程是 x = 2cosa． (2)
所以满足(1)、(2)的点P的坐标为(2cosa，sina)，消去a，即得
点P的轨迹方程为x2 + 4y2 = 4． ……………… 12分
说明： 设A(m，n)亦可类似地解决．
19．解 设
．
∵ 点P在直线OM上，
∴ 与
共线，而，
∴ x－2y=0即x=2y，有
．
………………
4分
∵ 
，
，
∴ 
= 5y2－20y+12
= 5(y－2)2－8． ……………… 8分
从而，当且仅当y=2，x=4时，
取得最小值－8，此时
，
，
．
于是
，
，
，
∴ 
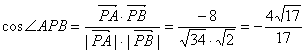．…………… 12分
20．解
填湖面积 填湖及排水设备费 水面经济收益 填湖造地后收益
x (亩) ax2 (元) bx cx
(Ⅰ) 收益不小于支出的条件可以表示为 cx ≥ ax2 + bx，
所以 ax2 + (b－c)x≤0， x[ax－(c－b)]≤0．
当 c－b≤0，即 
时，此时不能填湖造地；……… 3分
当 c－b＞0，即 
时，此时所填面积的最大值为
亩．
…………… 6分
(Ⅱ) 设该地现有水面m亩，今年填湖造地x亩，
则 
，
不等式左边是无穷等比数列(首项为x，公比q=0.99)的和，
故有 
， 即 
．
因此今年填湖造地面积最多只能占现有水面的0.25％．
…………… 12分
21． 证明：∵ 分子=(sin2acosa+cos2asina)－
(cos2acosa－sin2asina)－sina+cosa
= (2sinacos2a－sina)+cos2asina－(cos2acosa－cosa)+sin2asina
= sina(2cos2a－1)+sinacos2a+2sin2acosa+sin2asina
= 2sinacos2a+2sin2asina
= 2sina(sin2a+cos2a)， …………… 9分
分母=2sinacosa+2cos2a－1= (sin2a+cos2a)． …………… 11分
∴ 左边=2sina=右边，故等式成立． …………… 12分
22．解 由题意知，二次函数f(x)的对称轴为直线x=2，…… 2分
故f(x)在x∈(－∞，2
上单调递增，在[2，+∞上单调递减．
∵ 
，
， 且 0＜a＜1，
∴ 
，
，
∴ 
， …………… 6分
于是，得 
，
即 
．
……………
10分
∵ 
=
，
……………
12分
∴ 原不等式的解集为
．
…………… 14分