第一学期高三期末质量检测数学试题
数 学 试 题
第Ⅰ卷(选择题)
一、选择题 (本大题共12小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是正确的)
1、命题![]() ≤
≤![]() 是命题
是命题![]() ≥
≥![]() 或
或![]() ≤
≤![]()
A:充分非必要条件 B:必要非充分条件
C:充分必要条件 D:既非充分又非必要条件
|
|
|
|
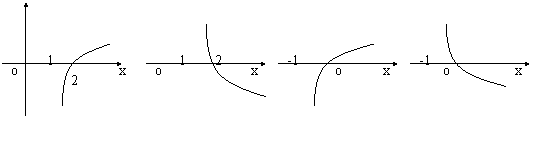
A B C D
3、从分别写有A、B、C、D、E的5张卡片中,任取2张,这2张卡片上的字母恰好按字母顺序相邻的概率是
A:![]() B:
B:![]() C:
C:![]() D:
D:![]()
4、要得到![]() 的图象,只需将
的图象,只需将![]() 的图象
的图象
A:向左平移![]() B:向右平移
B:向右平移![]()
C:向左平移![]() D:向右平移
D:向右平移![]()
5、若复数![]() 满足
满足![]() ≤0,则复数
≤0,则复数![]() 的最大值是
的最大值是
A:![]() B:
B:![]() C:
C:![]() D:3
D:3
6、已知函数![]() 的导数为
的导数为![]() ,且图象过点
,且图象过点![]() ,当函数
,当函数![]() 取得极大值
取得极大值![]() 时,
时,![]() 的值为
的值为
A:![]() B:
B:![]() C:
C:![]() D:
D:![]()
7、下列命题中正确结论的个数有
1) 若![]() ,则
,则![]() 是平行四边形。
是平行四边形。
数学试题 第1页 (共9页)
2) ![]() 与
与![]() 不共线
不共线![]() 对任何实数
对任何实数![]() 都有
都有![]()
3) ![]()
4) ![]() 在
在![]() 上的投影等于
上的投影等于![]() 在
在![]() 上的投影
上的投影![]()
![]()
A:0个 B:1个 C:2个 D:3个
8、 已知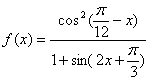 ,那么
,那么
A:![]() 既是奇函数又是偶函数
B:
既是奇函数又是偶函数
B: ![]() 没有最小正周期
没有最小正周期
C:![]() 没有最大值也没有最小值 D:
没有最大值也没有最小值 D:![]() 不是偶函数且最大值是
不是偶函数且最大值是![]()
9、已知定义在![]() 上的偶函数
上的偶函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,则
,则![]() 的
的![]() 的取值范围
的取值范围
A:![]() B:
B:![]() C:
C:![]() D:
D:![]()
10、在等差数列![]() 中,
中,![]() ,从第10项开始比1大,记
,从第10项开始比1大,记![]() ,则
,则![]() 的取值范围是
的取值范围是
A:![]() B:
B:![]() ≤
≤![]()
C:![]() D:
D:![]() ≤
≤![]()
11、若不等式![]() 在
在![]() 时恒成立,则实数
时恒成立,则实数![]() 的取值范围是
的取值范围是
A:![]() B:
B:![]() C:
C:![]() D:
D:![]()
![]()
![]()
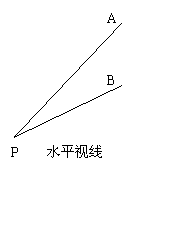
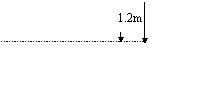
![]() 12、如下图所示,教室的墙壁上挂着一块黑板,它的上、下边缘分别在学生的水平视线上方2.4米和1.2米,现要求看黑板的竖直方向视角尽可能大些,则学生选择到墙壁的最佳距离为
12、如下图所示,教室的墙壁上挂着一块黑板,它的上、下边缘分别在学生的水平视线上方2.4米和1.2米,现要求看黑板的竖直方向视角尽可能大些,则学生选择到墙壁的最佳距离为
A:1.3米 B:1.5米
|
![]()
![]() C:1.7米
D:2.0米
C:1.7米
D:2.0米
 |
数学试题 第2页 (共9页)
![]() 第一学期高三期末质量检测
第一学期高三期末质量检测
数 学 试 题
第Ⅱ卷
注意事项:
1、 第Ⅰ卷答案填写在第Ⅱ卷的指定位置上
2、 用蓝色(或黑色)钢笔和圆珠笔将答案直接写在试卷上
| 学 校 |
|
|
3、 答卷前将密封线内的项目填写清楚,并在试卷右上角填上座位号
4、第Ⅰ卷答题栏
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 |
|
|
|
|
|
|
|
|
|
|
|
|
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 得 分 |
|
| 17 | 18 | 19 | 20 | 21 | 22 |
|
|
|
|
|
|
|
| ||||
| 班 级 |
|
|
| 得分 |
| ||
|
|
|
13、一批灯泡共400只,其中20W,40W,60W的数目比为![]() ,现用分层抽样产生一个容量为40的样本,三种灯泡依次抽取的个数为_____ _____ ______。
,现用分层抽样产生一个容量为40的样本,三种灯泡依次抽取的个数为_____ _____ ______。
14、设![]() 是圆
是圆![]() 的动点,若不等式
的动点,若不等式![]() ≥0恒成立,则
≥0恒成立,则![]() 的取值范围是__________
的取值范围是__________
| 姓 名 |
|
|
15、老师给出一个函数![]() ,四个学生甲、乙、丙、丁各指出这个函数的一个性质
,四个学生甲、乙、丙、丁各指出这个函数的一个性质
甲:对于![]() ,都有
,都有![]() 乙:在
乙:在![]() 上函数单调递减
上函数单调递减
丙:在![]() 上函数单调递增 丁:
上函数单调递增 丁:![]() 不是函数的最小值
不是函数的最小值
如果其中恰有三人说得正确,请写出这样的一个函数解析式_______________
16、64个正数排成8行8列,如下所示
![]()
![]() …………
………… ![]()
| 考生号 |
|
|
![]()
![]() …………
………… ![]()
… … …………. …
![]()
![]() …………
………… ![]()
在符号![]() (1≤i≤8, 1≤j≤8)中,
(1≤i≤8, 1≤j≤8)中,![]() 表示该数所在的行数,
表示该数所在的行数,![]() 表示该数所在的列数,
表示该数所在的列数,
已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等),![]() ,
,
数学试题 第3页 (共9页)
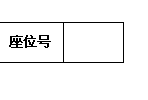
![]() ,
,![]() ,则
,则![]() 的通项公式为
的通项公式为![]() =____________
=____________
| 得分 |
| ||
|
|
|
17、(本小题满分12分)
|
|
| 900 | 1000 | 1100 |
|
|
|
|
|
试问哪家工厂生产的灯泡的质量好?
高三数学试题 第4页 (共9页)
18、(本小题满分12分)
在直角坐标系中,设矩形![]() 的顶点按逆时针顺序依次为
的顶点按逆时针顺序依次为![]()
![]() ,其中
,其中![]()
1) 求矩形在第一象限部分的面积![]()
2) 讨论函数![]() 的单调性
的单调性
高三数学试题 第5页 (共9页)
![]() 19、(本小题满分12分)
19、(本小题满分12分)
已知数列![]() 的通项公式
的通项公式![]() 是关于
是关于![]() 的不等式
的不等式![]() 的解集中整数的个数
的解集中整数的个数
1) 求数列![]() 的通项公式
的通项公式![]()
2) 设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]()
高三数学试题 第6页 (共9页)
![]() 20、(本小题满分12分)
20、(本小题满分12分)
在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() ,某公司每月最多生产100台报警系统装置,生产
,某公司每月最多生产100台报警系统装置,生产![]() 台的收入函数为
台的收入函数为![]() (单位:元),其成本函数为
(单位:元),其成本函数为![]() (单位:元),利润是收入与成本之差
(单位:元),利润是收入与成本之差
1) 求利润函数![]() 与边际利润函数
与边际利润函数![]()
2) 利润函数![]() 与边际利润函数
与边际利润函数![]() 是否具有相同的最大值?
是否具有相同的最大值?
3) 你认为本题中边际利润函数![]() 取最大值的实际意义是什么?
取最大值的实际意义是什么?
高三数学试题 第7页 (共9页)
21、(本小题满分12分)
设![]() 定义域为
定义域为![]() ,且
,且![]() ,如果
,如果![]() 为奇函数,当
为奇函数,当![]() 时,
时,![]()
1) 求![]()
2) 当![]() ,求
,求![]() 的表达式
的表达式
3) 是否存在这样的正整数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 有解?
有解?
高三数学试题 第8页 (共9页)
22、(本小题满分14分)
已知点![]() 和动点
和动点![]() 满足
满足![]() 是
是![]() ,
,![]() 的等差中项
的等差中项
(1) 求![]() 点的轨迹方程
点的轨迹方程
(2) 设![]() 点的轨迹为曲线
点的轨迹为曲线![]() 按向量
按向量![]() 平移后得到曲线
平移后得到曲线![]() ,曲线
,曲线![]() 上不同的两点
上不同的两点![]() 的连线交
的连线交![]() 轴于点
轴于点![]() ,如果
,如果![]() (
(![]() 为坐标原点)为锐角,求实数
为坐标原点)为锐角,求实数![]() 的取值范围。
的取值范围。
(3) 在(2)的条件下,如果![]() 时,曲线
时,曲线![]() 在点
在点![]() 处的切线的交点为R,求证:R在一条定直线上。
处的切线的交点为R,求证:R在一条定直线上。
高三数学试题 第9页 (共9页)
汕头市潮南区2003-2004学年度第一学期高三期末质量检测数学试题
参考答案及评分标准
一、选择题
1-12:ACBAB CBDBD DC
二、填空题
13、_20__ _15_ _5_。
14、![]()
15、![]()
16、![]()
三、解答题
17、(本小题满分12分)
解:哪家工厂的灯泡寿命期望值大,哪家的灯泡的质量就好,
由期望的定义有
![]() ……………2分
……………2分
![]() ……………4分
……………4分
由于两厂灯泡的期望值相等,因此甲、乙两厂的生产水平相当,
![]() 这就需要进一步考察两家灯泡的质量生产的稳定性,即看哪家工
这就需要进一步考察两家灯泡的质量生产的稳定性,即看哪家工
厂的灯泡的寿命取值更集中一些,这就需要比较其方差,方差小
的寿命值较稳定,灯泡质量较好, ……………6分
由方差的定义得:
![]() 8分
8分
![]() 10分
10分
由于![]() ,故乙厂生产的灯泡质量较甲稳定。
……………12分
,故乙厂生产的灯泡质量较甲稳定。
……………12分
18、解:1)由 ![]() ,有
,有![]() 则点
则点![]() 在第一象限内,
在第一象限内,
|
|
|
|
|
|
|
|
![]() (
(![]() )
……………8分
)
……………8分
2)由 ![]() ……………10分
……………10分
数学参考答案 第1页 (共6页)
![]()
![]()
![]()
![]()
![]() 函数
函数![]() 在区间
在区间![]() 上为单调递减函数 ……………12分
上为单调递减函数 ……………12分
19、解:1)原不等式等价于
![]() (1) 或
(1) 或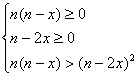 (2) ……………2分
(2) ……………2分
由(1)得 ![]()
由(2)得 ![]() ……………4分
……………4分
则原不等式的解集为 ![]() (
(![]() )
)
则 ![]() (
(![]() )
……………6分
)
……………6分
2)由 ![]()
则 ![]() ……………7分
……………7分
![]()
![]() (3)
(3)
![]() (4) ………9分
(4) ………9分
(3)-(4)得
![]()
![]()
![]()
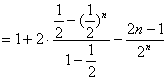
![]()
![]()
![]()
![]() ……………12分
……………12分
数学参考答案 第2页 (共6页)
20、解:(1)由题意可得:
![]()
![]() ………2分
………2分
![]()
![]()
![]()
![]() ……………4分
……………4分
(2) ![]()
![]()
![]() 当
当![]() 时,
时,![]() ……………6分
……………6分
又 ![]() 是减函数,所以当
是减函数,所以当![]() 时,
时,![]()
则 ![]() 与
与![]() 不具有相同的最大值
……………8分
不具有相同的最大值
……………8分
(3)边际利润函数![]() 当
当![]() 时取得最大值,说明生产第二
时取得最大值,说明生产第二
台与生产第一台的总利润差最大,即第二台报警系统利润最大。
![]() 是减函数,
……………10分
是减函数,
……………10分
说明随着产量的增加,每台利润与前一台利润相比较,利润
在减少。 ……………12分
21、解:(1)![]()
![]()
![]()
![]() 是以2为周期的周期函数
……………1分
是以2为周期的周期函数
……………1分
故 ![]()
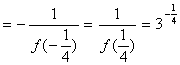 ……………3分
……………3分
(2)![]()
![]()
![]() ,
, ![]()
即 ![]()
数学参考答案 第3页 (共6页)
![]()
![]() ……………5分
……………5分
又 ![]()
故 ![]() ……………7分
……………7分
(3)由(2)知原不等式即为 ![]()
即 ![]() ①
①
![]() ……………8分
……………8分
ⅰ)若 ![]()
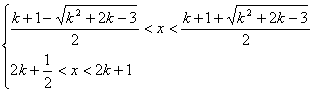
但 ![]()
![]() =
=![]()
![]() 此时
此时![]() ……………10分
……………10分
ⅱ)若![]() 时,则
时,则![]() ,①式无解
,①式无解
故不存在这样的实数![]() ……………12分
……………12分
22、解:(1)由题意可得
![]() ,
,
则 ![]()
![]()
![]()
![]() ……………2分
……………2分
又![]()
![]() 是
是![]() ,
,![]() 的等差中项
的等差中项
![]()
![]()
![]() =
=![]()
数学参考答案 第4页 (共6页)
整理得点![]() 的轨迹方程为
的轨迹方程为
![]() ……………4分
……………4分
(2) 由(1)知![]() :
:![]()
又 ![]()
![]() ,
,![]() 平移公式为
平移公式为
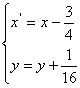 即
即 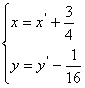
把它代入曲线![]() 的方程得到曲线
的方程得到曲线![]() 的方程为
的方程为
|
|
 即
即
|
|
|
![]()
由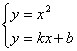 消去
消去![]() 得
得
![]()
![]()
令 ![]()
则 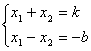 ,点
,点![]() 在抛物线上
在抛物线上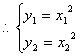
![]()
又![]() 为锐角
为锐角
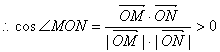 ……………8分
……………8分
数学参考答案 第5页 (共6页)
即 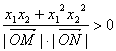
![]() ,又
,又![]()
![]() 得
得 ![]() 或
或![]() ……………10分
……………10分
(3)
当 ![]() 时,由(2)可得
时,由(2)可得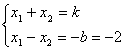
对![]() 求导可得
求导可得 ![]()
![]() 抛物线
抛物线![]() 在点
在点![]() 处的切线的
处的切线的
斜率分别为 ![]()
![]() 在点
在点![]() 处的切线方程分别为
处的切线方程分别为
![]()
![]() ………………12分
………………12分
由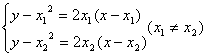
解得交点![]() 的坐标
的坐标![]()
满足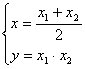 即
即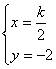
![]()
![]() 点在定直线
点在定直线 ![]() 上 ………………
14分
上 ………………
14分
高三数学参考答案第6页 (共6页)