第一学期高三数学期末质检复习题
一、选择题
1.若集合M={2,3},![]() ,又集合P=MUN,则集合P的真子集的个数共有( )
,又集合P=MUN,则集合P的真子集的个数共有( )
A.6个 B.7个 C.8个 D.以上答案都不正确
2.已知映射f:A→B,使集合B中元素y=x+1与集合A中元素x对应,要使映射f:A→B是一一映射,那么集合A,B可以是( )
A.A=R,B=R B.A=R,B={yy≧0}
C.A={xx≧0},B=R D.A={xx≧0},B={yy≧0}
3.已知f(x)是定义在R上的偶函数,且周期为2,当x∈[2,3]时,f(x)=x,则f(![]() )的值为( )
)的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.已知![]() 是第三象限角,且
是第三象限角,且![]() 那么
那么![]() 等于( )
等于( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
![]()
5.{an}是等差数列,S10>0,S11<0则使an<0最小的n的值为( )
A.5 B. 6 C. 7 D. 8
6.若a+b=a-b,则向量a与b的关系是( )
A. a=![]() 或b=
或b=![]() B.a=b C. a•b=0 D.以上都不对
B.a=b C. a•b=0 D.以上都不对
7.简单随机抽样,系统抽样,分层抽样之间的共同点是( )
A.都是从总体中逐个抽取
B.将总体分成n个部分,按事先确定的规则在各部分抽取
C.将总体分成几层,然后各层按比例抽取
D.抽样过程中每个个体被抽到的概率相等
8.已知直线![]() 垂直于平面
垂直于平面![]() ,直线m
,直线m![]() 平面
平面![]() 内,给出下列四个命题:
内,给出下列四个命题:
①若![]() ∥
∥![]() ,则
,则![]() ⊥m ②若
⊥m ②若![]() ∥m,则
∥m,则![]() ⊥
⊥![]()
③若![]() ⊥
⊥![]() ,则若
,则若![]() ∥m ④若
∥m ④若![]() ⊥m,则
⊥m,则![]() ∥
∥![]()
其中正确的命题是( )
A.③与④ B.①与③ C.②与④ D.①与②
9.已知双曲线![]() 与x轴的正半轴交于A点,F是它的左焦点,设B点的坐标为(0,b),且AB⊥BF,则双曲线的离心率是( )
与x轴的正半轴交于A点,F是它的左焦点,设B点的坐标为(0,b),且AB⊥BF,则双曲线的离心率是( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2),若x1+x2=6,则AB的中点M到抛物线的准线的距离等于( )
A.5 B. 4 C. 3 D. 2
11.定义运算a*b为:a*b=![]() 则关于x的函数f(x)=
则关于x的函数f(x)=![]() 的取值范围是( )
的取值范围是( )
A.![]() B.(0,1) C.
B.(0,1) C. ![]() D.[1,+∞)
D.[1,+∞)
12.四面体的顶点和各棱中点共10个点,从其中取4个不同的点,不共面的取法共有( )
A.150种 B.147种 C.144种 D.141种
二、填空题
13.(理)设复数![]() 满足
满足![]() _______
_______
(文)曲线y=![]() 上有一点P,曲线在点P处的切线的倾斜角为135°,则P点坐标为_______________
上有一点P,曲线在点P处的切线的倾斜角为135°,则P点坐标为_______________
14.设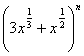 展开式中的各项的系数之和为A,各项的二项式系数和为B,若A+B=272,则展开式中的
展开式中的各项的系数之和为A,各项的二项式系数和为B,若A+B=272,则展开式中的![]() 项的系数是________
项的系数是________
15.将一个直角三角形沿斜边上的高折成直二面角后两直角边的夹角为![]() ,则
,则![]() 的最小值是_______________
的最小值是_______________
16.已知函数y=f(x)满足f(4)=2 ,f ’(4)= —2,则![]() 的值等于__________
的值等于__________
三、解答题
17.已知向量a=(cos![]() x,sin
x,sin![]() x),b=(cos
x),b=(cos![]() ,—sin
,—sin![]() )且x∈[0,
)且x∈[0,![]() ]
]
(1)求a·b及∣a+b∣
(2)若f(x)=![]() ∣a+b∣的最小值是-
∣a+b∣的最小值是-![]() ,求实数入的值
,求实数入的值
18.15名新生中有3名特长生,随机将15名新生平均分配到3个班组中去
(1)每班级各分配到一名特长生的概率是多少?
(2)3名特长生分配到同一班级的概率是多少?
19.已知函数f(x)=16x3-20ax2+8a2x-a3,其中a≠0,求f(x)的极大值与极小值。
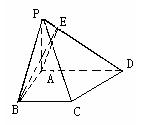 20.如图,在四棱锥p-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角
20.如图,在四棱锥p-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角
(1)若AE⊥PD,E为垂足,求证:BE⊥PD;
(2)求异面直线AE与CD所成角的大小,(用反三角函数表示)
21.某地现有居民住房的总面积为a平方米,其中需要拆除的旧房面积刚好占一半,当地有关部门决定在每年拆除一定相同数量旧房的情况下,同时以10%的增长率建设新房。
(1)如果10年后该地区住房面积正好比目前翻一番,那么每年应拆除的旧房面积是多少?
(2)过10年还未拆除的旧房面积占当时住房总面积的百分比是多少?(参考数据:1.110≈2.6)
22.已知椭圆的中心在原点,焦点在x轴上,一个顶点为A(0,-1),且其右焦点到直线x-y+2![]() =0的距离为3
=0的距离为3
(1)求椭圆方程;
(2)直线![]() (斜率不为0)与椭圆交于M、N两点,且∣AM∣=∣AN∣,求
(斜率不为0)与椭圆交于M、N两点,且∣AM∣=∣AN∣,求![]() 的斜率的取值范围。
的斜率的取值范围。
参考答案
一、B A C B B C D D B B C D
二、13(理)![]() (文)(
(文)(![]() ); 14. 1 15.
); 14. 1 15.![]() ; 16. 10
; 16. 10
三、17.(1)![]()
![]()
![]()
![]()
(2) 由(1)得
![]()
①当![]() 时,
时,![]()
②当![]() 时,
时,![]() 令
令![]() ∴
∴![]()
③当![]() 时,
时,![]() 令
令![]() 矛盾
矛盾
综上所述,只有![]()
18.解:(1)每个班级分到1名特长生,共有![]() 种不同的方法,将15名学生平均分到3个班级共有
种不同的方法,将15名学生平均分到3个班级共有![]() 种不同方法,每班分配到1名特长生的概率是
种不同方法,每班分配到1名特长生的概率是
![]()
(2)3名特长生都分到甲班共有![]() 种方法;乙班从剩下的10名之中选5名,共有
种方法;乙班从剩下的10名之中选5名,共有![]() 种方法;剩下的5名给丙班,共有
种方法;剩下的5名给丙班,共有![]() 种不同分法,同理,3名特长生都分到乙班,丙班方法数均为
种不同分法,同理,3名特长生都分到乙班,丙班方法数均为![]() , ∴3名特长生都分到同一班级的概率为
, ∴3名特长生都分到同一班级的概率为
![]()
19.解:![]()
![]()
由![]() 得
得![]()
![]()
当![]() 时
时
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大 | ↘ | 极小 | ↗ |
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
当![]() 时
时
|
|
|
|
|
|
|
|
| + | 0 | — | 0 | + |
|
| ↗ | 极大 | ↘ | 极小 | ↗ |
 当
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
20.解(9A)
(1)如右图:PA⊥平面ABCD
∴PA⊥AB 再由AB⊥AD,得AB⊥平面PAD ∴AB⊥PD
又∵AE⊥PD ∴PD⊥平面ABE 故BE⊥PD
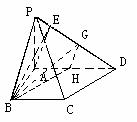
(2)设G,H分别为DE,AD的中点,连结BH、HG、GB,易知DH平行且等于CB ∴BH∥CD ∵G、H分别为ED、AD的中点 ∴HG∥AE,则∠BHG或它的补角就是异面直线AE、CD所成的角
而HG=![]() AE=
AE=![]() BH=
BH=![]()
![]()
在△BHG中,![]() ∴
∴![]()
所以异面直线AE、CD所成的角大小为![]()
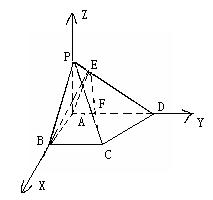
(9B)(1)∵PA⊥面ABCD,且∠BAD=90° ∴AB、AD、AP两两垂直
以![]() 、
、![]() 、
、![]() 为x、y、z轴建立空间直角坐标系
为x、y、z轴建立空间直角坐标系
则A(0,0,0) C(a,a,0) D(0,2a,0) B(a,0,0) P(0,0,![]() a)
a)
∵PA⊥面ABCD ∴∠PDA为PD和底面所成角,即∠PDA=30°
∴AE=a 作EF⊥AD, F为垂足
∴EF=![]() a ,AF=
a ,AF=![]() a
∴E(0,
a
∴E(0,![]() a,
a,![]() a)
a)
∵![]() =(-a,
=(-a,![]() a,
a,![]() a)
a) ![]() (0,2a,-
(0,2a,-![]() a)
a)
由![]() 0+a2+
0+a2+![]() a•(-
a•(-![]() a)=0
a)=0
 ∴
∴![]()
(2)![]() (-a,a,0)
(-a,a,0) ![]()
![]() a
a
![]() (0,
(0,![]() a,
a,![]() a)
a) ![]() a
a
![]()
![]() a2
a2
∴![]()
∴异面直线AE和CD所成角为![]()
21.解(1)设每年应拆除的旧房面积为x(m2),第n年后的住房面积为an,则
![]()
![]()
![]()
![]()
……
![]()
![]()
∴![]()
即 每年应拆除的旧房面积是![]()
(2)由(1)知,过10年还未拆除的旧房面积为![]()
故所求的百分比为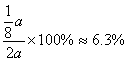
答:略
22.解:
(1)设椭圆方程为![]()
由题可知![]() 设右焦点为F(c,0) (c>0)
设右焦点为F(c,0) (c>0)
∴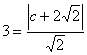 ∴
∴![]()
∴![]()
∴椭圆方程为![]()
(2)设直线![]() 的方程为
的方程为![]()
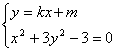 得
得 ![]()
△![]()
得![]()
即 ![]() ………………①
………………①
设直线与椭圆的交点为![]() 、
、![]()
∴![]()
令MN的中点为![]()
∴![]() ,
,![]()
由∣AM∣=∣AN∣知△AMN为等腰三角形
∵AP⊥MN
∴![]()
即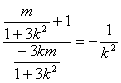
得 ![]() …………………………②
…………………………②
②代入①得 ![]()
∴![]()
∴![]()